3. Асимптоты гиперболы.

Определение 5. Прямая y=kx+m называется наклонной асимптотой кривой y = f(x) при х → +∞, если

. (9)

Аналогично определяется асимптота при х → –∞. Докажем, что прямые

(10)

являются асимптотами гиперболы (4) при х → ±∞.

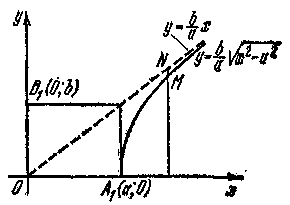
_{Рис. 3}

Так как прямые (10) и гипербола (4) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 3). Напишем уравнения прямых (10) и гиперболы (4), соответствующие первой четверти:

,

.

Положив и , найдем

Следовательно, прямые (10) являются асимптотами гиперболы (4).

Отметим, что асимптоты (10) являются продолжениями диагоналей прямоугольника, стороны которого параллельны осям Ох и Оу и равны соответственно 2а и 2b, а его центр находится в начале координат.

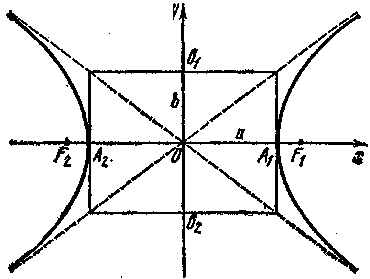
Рис. 4

При этом ветви гиперболы расположены внутри вертикальных углов, образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис. 4).

4. Эксцентриситет гиперболы.

Определение 6. Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси и обозначается буквой ε:

(11)

5. Сопряженная гипербола. Рассмотрим уравнение вида

. (12)

При переходе к новой системе координат, полученной в результате поворота осей старой системы вокруг начала координат на угол α = 90° (или α = –90°), уравнение (12) преобразуется в уравнение гиперболы

Следовательно, кривая, определяемая уравнением (12), есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а – на оси Ох.

Две гиперболы, которые определяются уравнениями

и

в одной и той же системе координат и при одних и тех же значениях а и b, называются сопряженными друг с другом.

6. Равносторонняя гипербола.

Определение 7. Гипербола называется равносторонней, если длины ее полуосей равны между собой, т.е. а=b. В этом случае уравнение гиперболы принимает вид

,

или

. (13)

Равносторонняя гипербола определяется одним параметром а и асимптотами являются биссектрисы координатных углов

_.

У всех равносторонних гипербол один и тот же эксцентриситет

Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат Ox'y', полученной в результате поворота осей старой системы вокруг начала координат на угол α = –45° (рис. 5). Составим уравнение равносторонней гиперболы относительно новой системы координат Ох'у'.

Учитывая равенство (13), получим x'y' = а²/2. (14)

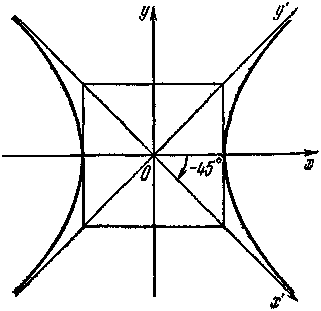
_{Рис. 5}

Определение 8. Уравнение (14) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.

Из уравнения (14) следует, что переменные х' и у' – величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратной пропорциональной зависимости.

Если центр гиперболы находится не в начале координат, а в точке О'(х₀; у₀), а оси гиперболы параллельны осям координат, то уравнение гиперболы будет иметь вид

или (15)

Это уравнения гиперболы со смещенным центром.