УЧЕБНЫЙ КОМПЛЕКС

ПРЕДМЕТ:

«ВЫСШАЯ МАТЕМАТИКА»

ТЕМА № 2.

«ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ».

Преподаватель Кононова М.П.

I. «векторы на плоскости

И В ПРОСТРАНСТВЕ».

МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО

ПОВТОРЕНИЯ И ИЗУЧЕНИЯ.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Тема «Векторы на плоскости и в пространстве» достаточно полно и подробно изучается в школьном курсе математики, причем, отдельно рассматриваются вопросы, связанные со свойствами векторов на плоскости, и затем расширяются знания о векторах при рассмотрении свойств векторов в пространстве.

Именно поэтому студентам предлагается самостоятельно повторить уже изученный материал по приведенным вопросам:

1.Определение вектора, его изображение и обозначение.

2.Основные виды векторов (определения и изображение).

3.Абсолютная величина вектора, направляющие косинусы вектора.

4.Координаты вектора – определение, правило нахождения, примеры.

5.Действия над векторами, заданными своими координатами (правила и примеры).

6.Свойства перпендикулярных, коллинеарных и компланарных векторов (теоремы и примеры на применение).

7.Орты на плоскости и в пространстве (определения и изображение)

Для составления конспекта, который затем используется при выполнении практического задания, и не только, студентам предлагается использовать как учебную литературу по высшей математике, так и школьные учебники. Однако, кроме ранее изученных вопросов, в перечень входят вопросы, непредусмотренные школьной программой, их немного, они достаточно просты для понимания и изучения.

Предлагаемый текст не содержит примеров. Студенты должны самостоятельно подобрать примеры к рассматриваемым определениям, теоремам, свойствам.

Данная тема также используется при решении задач по теме «Аналитическая геометрия», что позволяет также проследить связь между разделами математики, и показать, что всегда можно найти более простой способ решения той или иной задачи.

1). Введение.

Понятие вектора находит свое применение и в математике, и в физике, и в других науках.

Знакомство с ними началось еще в школе: рассматривались векторы на плоскости, а затем и в пространстве.

При изучении различных разделов физики, механики и других технических дисциплин встречаются величины, которые вполне характеризуются заданием их численных значений – это так называемые скалярные («скаляр» - латинское - «число») величины. Существуют, однако, и такие величины, для определения которых задания только их численных значений недостаточно. Необходимо также знать их направления в пространстве – эти величины называют векторными.

Примеры:

Скалярные величины – длина, площадь, объем, масса, температура.

Векторные величины – сила, скорость, ускорение, напряженность магнитного поля.

2). Понятие вектора.

В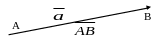 ектор – это направленный отрезок, т.е., отрезок, один конец которого считают его началом, а другой – концом (его указывают стрелкой).

Основные определения:

1. Абсолютной величиной, или модулем, вектора называется длина отрезка, изображающего вектор: .

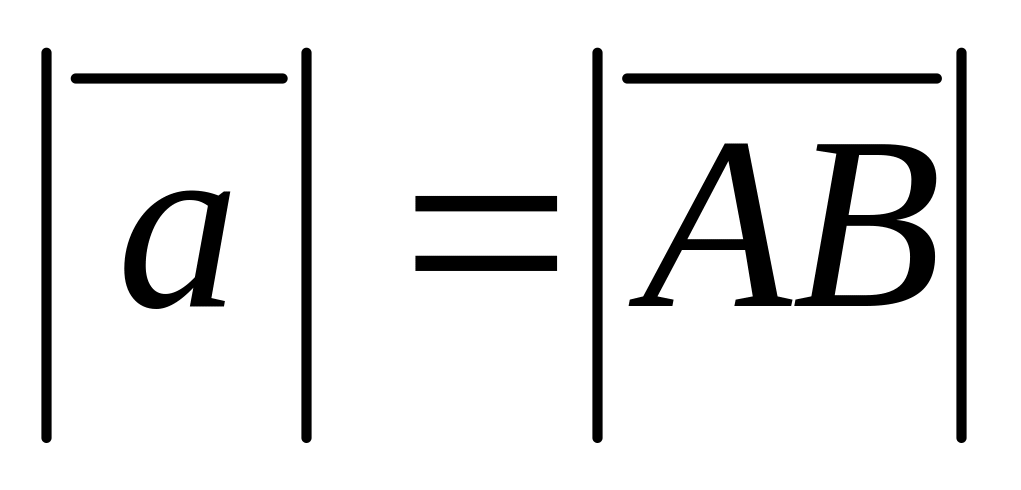2. Вектор, конец и начало которого совпадают, называется нулевым – обозначается 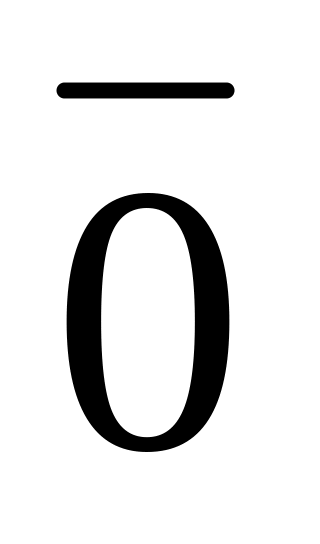, его абсолютная величина .

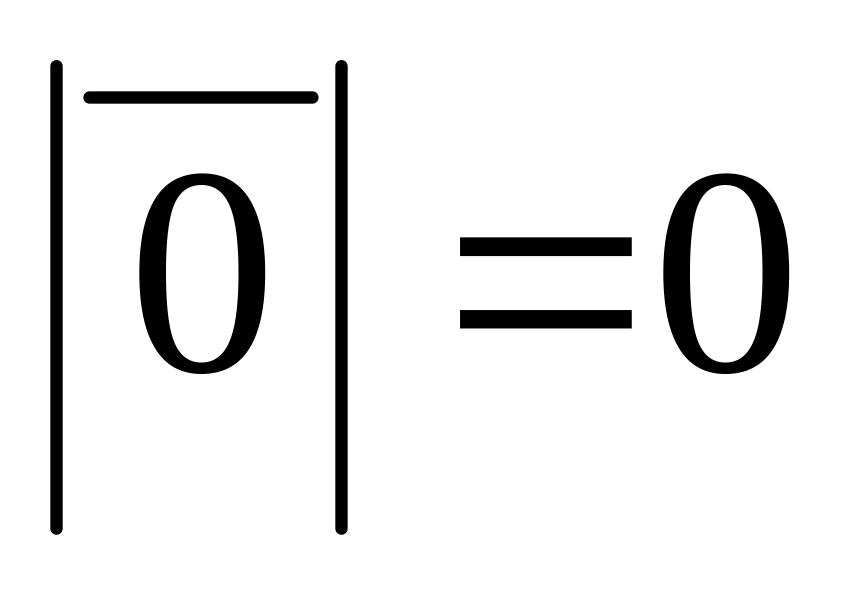3. Векторы 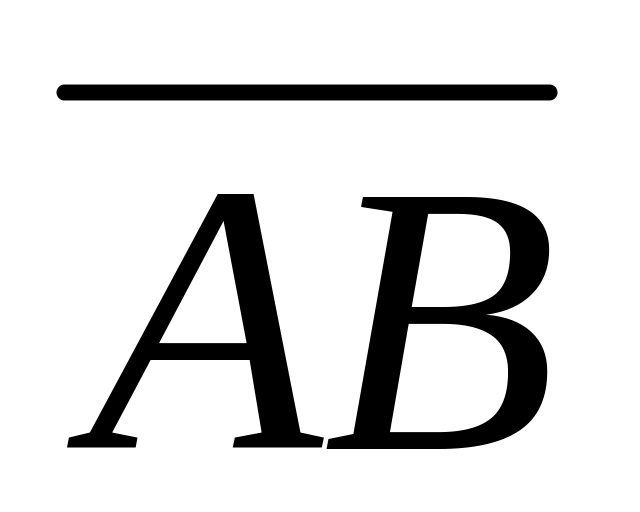и называются одинаково (противоположно) направленными, если полупрямые АВ и CD одинаково (противоположно) направлены , .

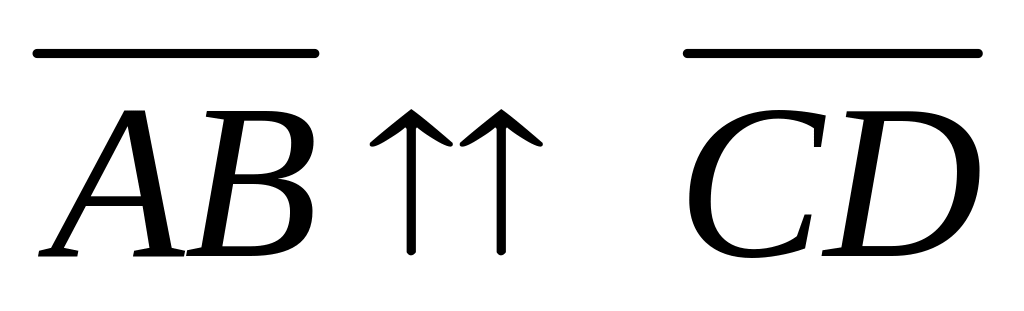4. Два ненулевых вектора называются равными, если они равны по абсолютной величине и одинаково направлены: ,

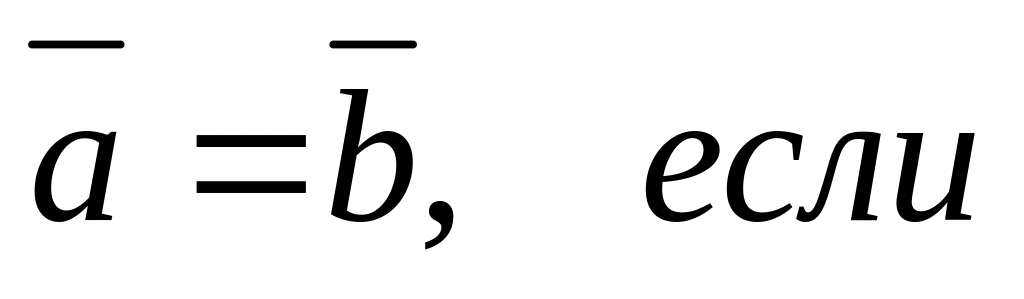
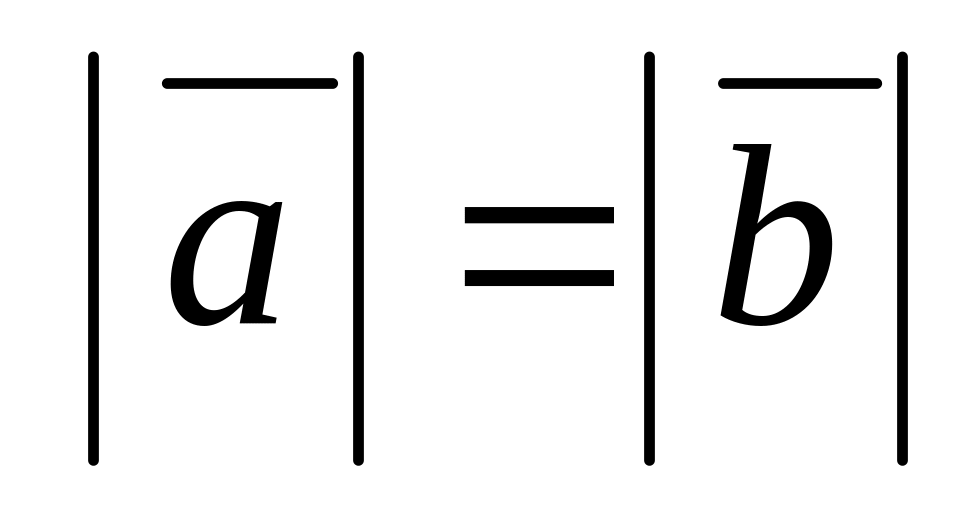5. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

6. Три ненулевых вектора называются компланарными, если они параллельны одной плоскости.

7. Углом между двумя векторами называется угол между пересекающимися прямыми, параллельными этим векторам.

8. Косинусы углов между векторами 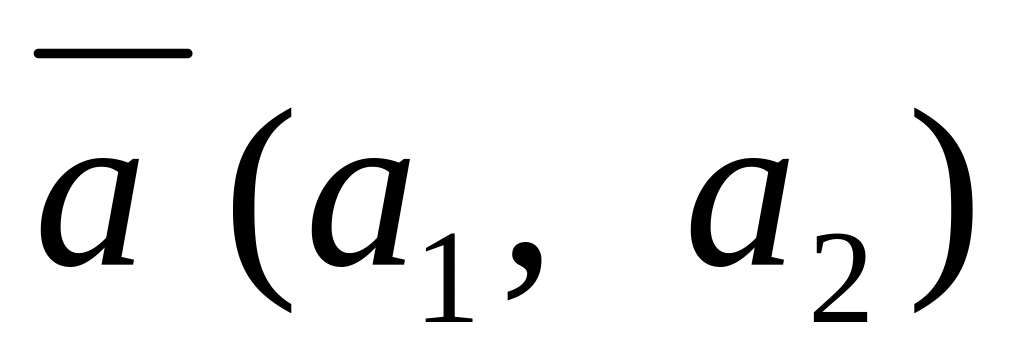и базисными векторами 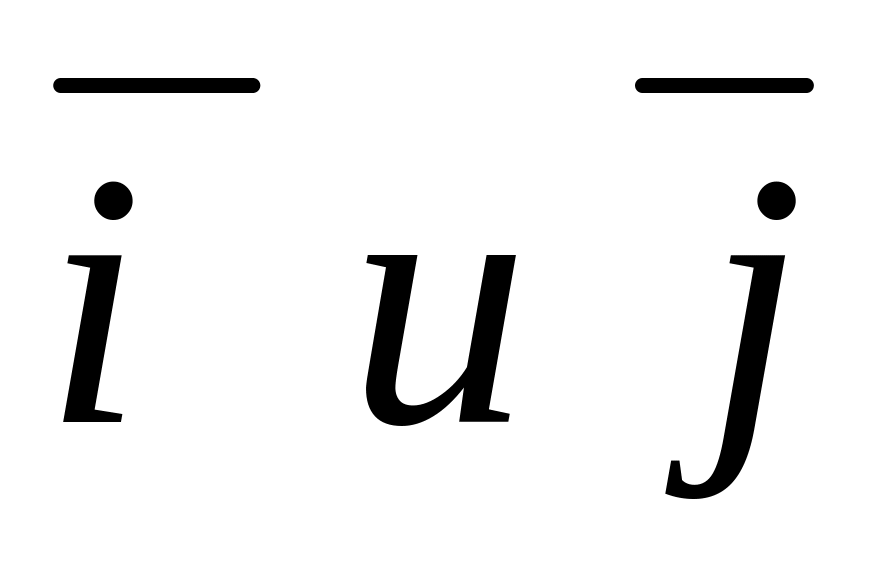называются направляющими косинусами вектора и вычисляются по формулам

Направляющие косинусы любого вектора связаны равенством

9. Единичным вектором называется вектор, абсолютная величина которого равна 1.

Векторы – называют ортами (или базисными), если они единичные, т.е.,

, а

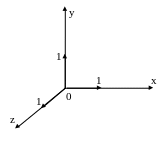
их направления совпадают с положительными направлениями осей координат:

.