Міністерство освіти і науки, молоді та спорту України

Національний технічний університет України

«Київський політехнічний інститут»

Х І М І Я

Навчальний посібник

для студентів

технічних напрямів підготовки

Рекомендовано Методичною радою НТУУ «КПІ»

Київ НТУУ «КПІ» 2011

Хімія. Навчальний посібник для студентів технічних напрямів підготовки / Уклад.: О. М. Князєва, В. А. Потаскалов. – К.: 2011. – 160 с.

Гриф надано Методичною радою НТУУ „КПІ”

(Протокол № 10 від 16.06.2011 р.)

Х І М І Я

Навчальний посібник

для студентів

технічних напрямів підготовки

Укладачі: Князєва Олена Миколаївна, канд. хім. наук, доц.

Потаскалов Вадим Анатолійович, канд. хім. наук, доц.

Відповідальний редактор: О.О. Андрійко докт. хім. наук, проф., зав. кафедри ЗНХ

Рецензенти:

Лисін В.І., канд. хім. наук, доц. кафедри електрохімічної енергетики та хімії

Київського національного університету технологій та дизайну КНУТД

Манчук Н.М., канд. техн. наук, доц. кафедри хімії і хімічної технології

інституту екологічної безпеки Національного авіаційного університету

З а редакцією укладачів

Електронне видання

ЗМІСТ

ЗМІСТ 3

РОЗДІЛ І. БУДОВА ТА ВЛАСТИВОСТІ РЕЧОВИН 5

1. ОСНОВНІ ПОНЯТТЯ ХІМІЇ 5

Кількісні характеристики речовини 5

4. КЛАСИ НЕОРГАНІЧНИХ СПОЛУК 39

Аналіз рівняння, що пов`язує G, H та S 54

Вплив температури на напрямок перебігу реакції 55

РОЗДІЛ ІІІ. РОЗЧИНИ 77

7. ПРИРОДА РОЗЧИНІВ ТА СПОСОБИ ВИРАЖЕННЯ ЇХ СКЛАДУ 77

Способи вираження складу розчинів 80

РОЗДІЛ ІV. ОКИСНО-ВІДНОВНІ РЕАКЦІЇ 108

РОЗДІЛ V. ЕЛЕКТРОХІМІЧНІ ПРОЦЕСИ 119

10. ГальванічНІ елементи 119

Вимірювання електродних потенціалів 126

12. КОРОЗІЯ МЕТАЛІВ ТА СПЛАВІВ 137

Класифікація процесів корозії за механізмом їх перебігу 137

Фактори, що сприяють корозії 139

Способи захисту від корозії 141

СПИСОК ЛІТЕРАТУРИ 160

5.  Григор`єва В.В., Самійленко В.М., Сич А.М. Загальна хімія: Підручник – К.: Вища шк., 1991. – 431 с., ISBN 5-11-003667-5. 160

161

РОЗДІЛ IV. ОКИСНО-ВІДНОВНІ РЕАКЦІЇ 107

РОЗДІЛ V. ЕЛЕКТРОХІМІЧНІ ПРОЦЕСИ 118

ЗМІСТ 3

РОЗДІЛ І. БУДОВА ТА ВЛАСТИВОСТІ РЕЧОВИН 5

1. ОСНОВНІ ПОНЯТТЯ ХІМІЇ 5

Кількісні характеристики речовини 5

4. КЛАСИ НЕОРГАНІЧНИХ СПОЛУК 39

Аналіз рівняння, що пов`язує G, H та S 54

Вплив температури на напрямок перебігу реакції 55

РОЗДІЛ ІІІ. РОЗЧИНИ 77

7. ПРИРОДА РОЗЧИНІВ ТА СПОСОБИ ВИРАЖЕННЯ ЇХ СКЛАДУ 77

Способи вираження складу розчинів 80

РОЗДІЛ ІV. ОКИСНО-ВІДНОВНІ РЕАКЦІЇ 108

РОЗДІЛ V. ЕЛЕКТРОХІМІЧНІ ПРОЦЕСИ 119

10. ГальванічНІ елементи 119

Вимірювання електродних потенціалів 126

12. КОРОЗІЯ МЕТАЛІВ ТА СПЛАВІВ 137

Класифікація процесів корозії за механізмом їх перебігу 137

Фактори, що сприяють корозії 139

Способи захисту від корозії 141

СПИСОК ЛІТЕРАТУРИ 160

5.  Григор`єва В.В., Самійленко В.М., Сич А.М. Загальна хімія: Підручник – К.: Вища шк., 1991. – 431 с., ISBN 5-11-003667-5. 160

161

РОЗДІЛ І. БУДОВА ТА ВЛАСТИВОСТІ РЕЧОВИН

1. ОСНОВНІ ПОНЯТТЯ ХІМІЇ

Хімія вивчає: 1) якісний та кількісний склад речовини; 2) її будову; 3) фізичні властивості речовини (температури плавлення та кипіння, магнітні та спектральні властивості, густину, твердість, тепло- та електропровідність тощо); 4) хімічні властивості речовини, тобто її здатність взаємодіяти з іншими речовинами; 5) хімічні реакції, тобто процеси, внаслідок яких відбувається перетворення одних речовин на інші.

Речовина – це форма матерії, яка складається з частинок, що мають масу спокою, а саме з атомів, молекул та йонів.

Атом - це найменша хімічно неподільна частинка хімічного елемента.

Хімічний елемент - це вид атомів з однаковим зарядом ядра. Наприклад, хімічний елемент ферум Fe - це сукупність атомів із зарядом ядра "+26", хімічний елемент сульфур S - це сукупність атомів із зарядом ядра "+16". Хімічні властивості елемента визначаються електронною будовою атомів цього елемента.

Молекула - це найменша частинка речовини, яка здатна існувати самостійно, зберігаючи хімічні властивості речовини. Наприклад, молекули Н₂ , СО₂, Р₄, S₈, Не, C₂H₆, C₆H₆ тощо.

Але більшість твердих неорганічних речовин не мають молекулярної будови. Наприклад, кристал кварцу SiO₂ складається з атомів сіліцію та оксигену, а кристал натрій хлориду NaCl - з йонів натрію Na⁺ та хлорид-йонів СІ^–, які з'єднані між собою у певному порядку. Такі неіснуючі частинки, як SiO₂ та NaCl, що лише відображають склад речовини, називають умовними молекулами.

Будь-яка речовина складається з формульних одиниць (ФО), до яких належать реально існуючі атоми, молекули, йони та умовні молекули.

Проста речовина утворена з атомів одного хімічного елемента, а хімічна сполука - з атомів різних хімічних елементів. Наприклад, проста речовина водень складається з молекул Н₂, утворених атомами тільки одного хімічного елемента – гідрогену. Проста речовина залізо Fe утворена тільки атомами феруму, а хімічна сполука кальцій оксид СаО – атомами різних хімічних елементів, а саме, атомами кальцію та оксигену.

Кількісні характеристики речовини

Масу речовини позначають буквою m(В), а абсолютну масу окремого атома або молекули – m₀(В). Наприклад, маса порції водню дорівнює m(Н₂)=10 г, а маса атома гідрогену m₀(Н)=1,67·10^-24 г, маса молекули водню m₀(H₂)=3,34·10^-24г. Через те, що абсолютними масами атомів та молекул користуватись незручно, за одиницю маси атомів та молекул було прийнято атомну одиницю маси.

Атомна одиниця маси (а.о.м.) - це 1/12 частина маси атома ізотопу карбону ¹²С.

Відносна атомна маса хімічного елемента А_r(В) – це відношення маси атома хімічного елемента до 1/12 маси атома карбону ¹²С.

(1.1)

Відносна молекулярна маса речовини M_r(В) - це відношення маси молекули речовини до 1/12 маси атома карбону ¹²С.

(1.2)

Відносні атомна та молекулярна маси – величини безрозмірні.

Наприклад, відносна атомна маса нітрогену дорівнює: A_r(N)=14, відносна молекулярна маса карбон (ІV) оксиду: М_r(СО₂) = A_r(C) + 2·A_r(O) = 44.

За одиницю кількості речовини прийнято моль. Моль - цe кількість речовини, що містить 6,02·10²³ ФО, тобто атомів, молекул або йонів.

Стала Авогадро дорівнює: N_A=6,02·10²³ моль^-1 і показує число ФО, що містяться в кількості речовини 1 моль, тобто число атомів, що містяться в 1 моль атомів, число молекул - в 1 моль молекул, число йонів - в 1 моль йонів.

Кількість речовини позначають буквою n(В), вимірюють у молях і розраховують за виразом:

моль, (1.3)

де N(B) – число формульних одиниць (ФО) у певній кількості речовини n(B).

Наприклад, n(СO₂)=0,5моль.

Число молекул, що містяться у цій кількості речовини, відповідно до (1.3) дорівнює:

N(СO₂) = n(СO₂) · N_A = 0,5 моль · 6,02·10²³ моль^–1 = 3,01·10²³.

Молярна маса речовини М(В) (маса кількості речовини 1 моль) - це відношення маси речовини до її кількості:

г/моль (1.4)

Молярна маса атомів – це виражена в грамах маса 1 моль атомів, що чисельно дорівнює відносній атомній масі, а молярна маса молекул – виражена в грамах маса 1 моль молекул речовини, що чисельно дорівнює відносній молекулярній масі. Наприклад, відносна атомна маса нітрогену дорівнює: A_r(N)=14, а молярна маса атомів нітрогену: M(N)=14 г/моль. Відносна молекулярна маса карбон(ІV) оксиду: M_r(CO₂) =44, а молярна маса його молекул: М(СО₂) =44 г/моль.

Знаючи молярну масу речовини та число ФО в кількості речовини 1 моль, можна розрахувати масу однієї ФО, тобто масу атома або молекули:

г (1.5)

Так, маса атома нітрогену дорiвнює: , маса молекули карбон(ІV) оксиду: .

Молярний об'єм газу V_М (об'єм кількості газу 1 моль) – це відношення об'єму газу V(B) до його кількості:

л/моль (1.6)

Молярний об'єм будь-якого газу за нормальних умов (н.у.) (Т=273К, р=101,3 кПа) дорівнює: V_М°=22,4 л/моль.

Вирази (1.3), (1.4) і (1.6) можна об`єднати, тоді матимемо:

, (1.7)

де m(B) – маса кількості речовини n(B), N(B) – число формульних одиниць, що містяться в цій кількості речовини, а V(B) – об`єм кількості газуватої речовини n(B).

З цього загального виразу можна знайти будь-яку з наведених величин.

Відносна густина одного газу В₁ за іншим В₂, яку позначають D(B₂) - це відношення густини цих газів ( ), тобто відношення мас однакових об’ємів газів (V(B₁)=V(B₂)), отже і відношення їх молярних мас (молярної маси газу В₁ до молярної маси газу В₂):

, (1.8)

звідки M(B₁)=М(В₂)·D(B₂). Якщо густину газу В₁ визначають відносно водню (D(H₂)), то молярна маса газу В₁ дорівнює: М(В₁)=М(H₂)·D(H₂)=2·D(H₂). Якщо густину газу визначають відносно повітря (D_пов), то M(B₁)=M_пов·D_пов , де М_пов - середня молярна маса повітря, що становить 29 г/моль.

Приклад 1. Маса газу об'ємом 5,6 л (н.у.) дорівнює 7 г. Обчисліть: а) молярну масу газу, б) його відносну молекулярну масу, в) масу молекули газу.

Розв'язання. а) Використовуючи співвідношення (1.7), знаходимо кількість речовини газу та його молярну масу:

,

б) Оскільки відносна молекулярна мaca речовини чисельно дорівнює її молярній масі, але є безрозмірною величиною, то M_r(B) = 28.

в) За виразом (1.5) маса молекули газу дорівнює:

.

Приклад 2: Кисень у лабораторії добувають під час термічного розкладу калій перманганату׃ 2KMnO₄ = K₂MnO₄ + MnO₂ + O₂. Обчисліть кількість, масу та об`єм за н.у. кисню, що утворюється за нагрівання KMnO₄ масою 474 г. Скільки молекул міститься в цій кількості кисню?

Розв'язання. Відносна молекулярна маса калій перманганату дорівнює сумі атомних мас елементів, що входять до складу молекули цієї речовини:

M_r(KMnO₄) = A_r(K) + A_r(Mn) +4A_r(O) = 39,1 + 54,9 + 4·16 = 158

Молярна маса калій перманганату чисельно дорівнює його відносній молекулярній масі: M(KMnO₄) = 158 г/моль

Визначимо кількість KMnO₄ масою 474 г, використовуючи співвідношення (1.7):

Згідно з рівнянням реакції з 2 моль KMnO₄ за нагрівання утворюється 1 моль О₂, а з 3 моль KMnO₄ – відповідно 1,5 моль О₂.

За виразом (1.7) знаходимо масу, об`єм за н.у. визначеної кількості кисню та число молекул, що містяться у цій кількості кисню:

m(O₂) = n(O₂) · M(O₂) = 1,5 моль · 32 г/моль = 48 г,

V⁰(O₂) = n(O₂) · V⁰_М = 1,5 моль · 22,4 л/моль = 33,6 л,

N(O₂) = n(O₂) · N_A = 1,5 моль · 6,02·10²³ моль^–1 = 9,03·10²³.

Приклад 3. Розрахуйте відносну густину карбон (ІV) оксиду за азотом.

Розв'язання. Згідно з виразом (1.8) :

.

Еквівалент речовини - це умовна частинка, яка в z* разів менша за формульну одиницю (ФО), і позначається . Число z* називається числом еквівалентності. У формульній одиниці міститься z* еквівалентів. Якщо z*=1, тоді еквівалентом речовини є її формульна одиниця.

Для хімічного елемента формульною одиницею є його атом, a z* дорівнює валентності елемента у сполуці. Отже, еквівалент елемента – це атом або його частка, що припадає на одиницю валентності елемента.

Для хімічної сполуки формульною одиницею є її молекула.

Кількість еквівалентів позначають буквою і вимірюють у молях, а молярну масу еквівалентів речовини, тобто масу кількості еквівалентів 1 моль, позначають і вимірюють у г/моль.

Співвідношення між кількістю еквівалентів та молярною масою еквівалентів речовини має вигляд:

, або (1.9)

Якщо речовина газувата, то користуються молярним об'ємом еквівалентів газу, тобто об’ємом кількості еквівалентів 1 моль , який вимірюють у л/моль:

, або (1.10)

Закон єквівалентів: Маси речовин, що беруть участь у хімічних реакціях, відносяться між собою, як молярні маси іх еквівалентів.

, або , (1.11)

звідки, (1.12)

Отже, кількість еквівалентів всіх учасників реакції дорівнює одна одній, а молярні маси еквівалентів – це маси кількості еквівалентів 1 моль, які без залишку взаємодіють між собою.

Якщо речовина газувата, то у виразі (1.11) замість молярної маси еквівалентів використовують молярний об'єм еквівалентів цієї речовини:

(1.13)

Молярна маса еквівалентів хімічного елемента дорівнює молярній масі елемента, поділеній на число еквівалентності:

(1.14)

За законом еквівалентів 1 моль еквівалентів одного елемента В₁ сполучаеться з 1 моль еквівалентів іншого елемента В₂ і при цьому утворюється 1 моль еквівалентів хімічної сполуки. Тому молярна маса еквівалентів сполуки дорівнює сумі молярних мас еквівалентів елементів ,з атомів яких складається молекула сполуки:

(1.15)

Оскільки проста речовина утворюється з атомів одного хімічного елемента, тому молярна маса еквівалентів простої речовини дорівнює молярній масі еквівалентів цього хімічного елемента, а молярний об`єм еквівалентів простої газуватої речовини дорівнює молярному об`єму еквівалентів хімічного елемента.

Приклад 4. Чому дорівнює: а) еквівалент і молярна маса еквівалентів хімічних елементів – гідрогену та оксигену; б) молярна маса еквівалентів простих речовин – водню (Н₂) та кисню (О₂); в) молярний об’єм еквівалентів водню та кисню; г) молярний об’єм еквівалентів гідрогену та оксигену?

Розв’язання.

а) Валентність гідрогену дорівнює I, а оксигену – II, число еквівалентності z* цих елементів становить відповідно 1 та 2.

Тому еквівалентом гідрогену є його атом (Н), а еквівалентом оксигену є атома оксигену ( ).

За виразом (1.14) молярна маса еквівалентів гідрогену дорівнює:

_,

а молярна маса еквівалентів оксигену дорівнює:

б) Оскільки молярна маса еквівалентів простої речовини дорівнює молярній масі еквівалентів хімічного елемента, то молярна маса еквівалентів водню становить 1 г/моль, а молярна маса еквівалентів кисню – 8 г/моль.

в) Згідно з співвідношенням (1.7) визначимо кількості простих речовин водню та кисню, маса яких дорівнює відповідно молярній масі еквівалентів водню та молярній масі еквівалентів кисню, а об`єм – молярним об`ємам еквівалентів цих речовин:

,

.

Знаходимо об`єм (н.у.) розрахованих кількостей водню та кисню (1.7):

V⁰(Н₂) = n(Н₂) · V⁰_М = 0,5 моль · 22,4 л/моль = 11,2 л,

V⁰(O₂) = n(O₂) · V⁰_М = 0,25 моль · 22,4 л/моль = 5,6 л

Отже, молярний об`єм еквівалентів водню дорівнює 11,2 л/моль, а молярний об`єм еквівалентів кисню – 5,6 л/моль.

г) Оскільки молярний об`єм еквівалентів хімічного елемента дорівнює молярному об`єму еквівалентів простої речовини, яка складається з атомів цього елемента, то молярний об’єм еквівалентів гідрогену V⁰_М( Н) становить 11,2 л/моль, а молярний об’єм еквівалентів оксигену V⁰_М( O) – 5,6 л/моль.

Приклад 5. Під час згоряння металу масою 5 г утворюється метал оксид масою 9,44 г, в якому валентність металу дорівнює трьом. Розрахуйте а) еквівалент металу, б) молярну масу еквівалентів металу, в) молярну масу еквівалентів метал оксиду, г) молярну масу металу. Визначте, що це за метал.

Розв'язання.

а) Оскільки число еквівалентності металу співпадає з його валентністю, то еквівалентом металу є 1/3 його атома ( ).

б) За виразом (1.9) обчислюємо кількість еквівалентів оксигену, що знаходиться в утвореному оксиді, враховуючи, що маса оксигену дорівнює різниці між масою оксиду та масою металу: m(O) = 9,44 г – 5 г = 4,44 г;

Кількість еквівалентів металу дорівнює кількості еквівалентів оксигену (1.12):

Розрахуємо молярну масу еквівалентів металу (1.9):

в) Молярна маса еквівалентів метал оксиду дорівнює сумі молярних мас еквівалентів металу та оксигену (1.15):

.

г) Обчислюємо молярну масу металу (1.14):

, тому

За Періодичною системою елементів визначаємо, що це алюміній.

Приклад 6. Визначте а) молярну масу еквівалентів стануму, б) його валентність в станум хлориді SnCl_n з масовою часткою стануму ω(Sn)=45,56 % (0,4556 в частках від одиниці). Наведіть формулу сполуки.

Розв'язання. а) Масова частка елемента в сполуці – це відношення його маси до маси сполуки. Отже, масова частка стануму в станум хлориді дорівнює:

Звідки: m(Sn) = ω(Sn) · m(SnCl_n) =0,4556 · m(SnCl_n)

Сума масових часток всіх елементів в сполуці становить 1, тому масова частка хлору та його маса дорівнюють:

ω(Cl) = 1 – ω(Sn) = 1 – 0,4556 = 0,5444 ,

m(Cl) = ω(Cl) · m(SnCl_n) =0,5444 · m(SnCl_n)

Елемент хлор в хлоридах є одновалентним, тобто число еквівалентності z*(Cl)=1, тому молярна маса еквівалентів хлору дорівнює:

г/моль.

За законом еквівалентів (1.11) розрахуємо молярну масу еквівалентів стануму:

б) Число еквівалентності стануму в станум хлориді визначається за виразом (1.14):

Оскільки валентність елемента в сполуці співпадає з його числом еквівалентності, то валентність стануму в станум хлориді становить IV. Формула сполуки – SnCl₄.

Приклад 7. Під час розчинення заліза масою 7 г у хлоридній кислоті виділяється водень об'ємом 2,8 л (н.у.). Розрахуйте а) молярну масу еквівалентів феруму, б) валентність феруму та його еквівалент в солі, яка утворилась. Наведіть формулу солі.

Розв'язання.

а) Розрахувати молярну масу еквівалентів феруму можна двома способами:

I спосіб. За законом еквівалентів (1.13) розрахуємо молярну масу еквівалентів феруму, враховуючи, що молярний об’єм еквівалентів водню дорівнює молярному об’єму еквівалентів гідрогену, тобто становить 11,2 л/моль:

; ,

ІI спосіб. Кількість еквівалентів водню, виділеного внаслідок розчинення заліза у кислоті, дорівнює кількості еквівалентів гідрогену, витісненого з кислоти металом, а саме (1.10):

За виразом (1.12): .

Обчислимо молярну масу еквівалентів феруму (1.9):

б) Визначимо число еквівалентності феруму в солі (1.14):

;

Валентність феруму в солі дорівнює ІІ, його еквівалентом є атома ( ), а формула утвореної солі – FeCl₂.

2. Будова атомів

Атом хімічного елемента складається з позитивно зарядженого ядра та електронів із зарядом “-1”, які рухаються навколо ядра і утворюють електронну оболонку атома. У складі ядра знаходяться протони із зарядом “+1” та електронейтральні частинки – нейтрони. Протони та нейтрони мають загальну назву – нуклони. Заряд ядра атома обумовлений наявністю протонів у складі ядра.

Протонне число (порядковий номер) хімічного елемента чисельно дорівнює числу протонів, що містяться у складі ядра його атомів. Наприклад, протонне число натрію 11. Отже, в ядрі атомів натрію знаходяться 11 протонів.

Нуклонне число хімічного елемента дорівнює числу нуклонів, тобто сумарному числу протонів та нейтронів у складі ядра атома. Нуклонне число хімічного елемента – це найближче до його атомної маси ціле число. Так, атомна маса натрію A_r(Na)=22,7, а нуклонне число становить 23. Отже, ядро атома натрію складається з 23 нуклонів, а саме: з 11 протонів та 12 нейтронів.

Оскільки атом електронейтральний, то число електронів, які утворюють його електронну оболонку, дорівнює числу протонів у складі ядра атома. Так, в атомі натрію містяться 11 електронів.

Ядро атома не бере участь в хімічних реакціях. Це означає, що хімічні властивості елементів залежать лише від електронної будови їх атомів, тобто від структури їх електронних оболонок.

Сучасна теорія електронної будови атомів ґрунтується на уявленні про двоїсту, корпускулярно-хвильову природу мікрочастинок, в тому числі і електронів: електрон є матеріальною частинкою з певною масою та зарядом, але рух електронів має хвильову природу. Саме тому стан електронів в атомі вивчає не класична механіка, яка є механікою макрооб’єктів, а квантова механіка. Квантова механіка – це механіка мікрочастинок, яка враховує їх двоїсту природу. Основою квантової механіки є рівняння Шредінгера, яке в квантовій механіці відіграє таку ж роль, як закони Ньютона в класичній механіці. Рішенням рівняння Шредінгера є хвильова функція , як функція просторових координат х, у, z. Але фізичний зміст має не сама хвильова функція, а квадрат її модуля ², який характеризує ймовірність перебування електрона в певній точці простору, а ²·dv – в елементі простору dv навколо ядра атома. Частина простору навколо ядра атома, де ймовірність перебування електрона є найбільшою (90%), називається електронною хмарою. Таким чином, квантова механіка вказує не на точне знаходження електрона в атомі, а на ймовірність його перебування у просторі навколо ядра атома, тобто замінює поняття “траєкторія руху електрона” на поняття “електронна хмара”.

Рішення рівняння Шредінгера, тобто хвильова функція  містить безрозмірні цілочисельні параметри n, ℓ, m_ℓ – квантові числа.

Хвильова функція з конкретними значеннями квантових чисел n,ℓ,m_ℓ називається атомною орбіталлю АО.

Головне квантове число п характеризує повний запас енергії електрона на певному енергетичному рівні. Головне квантове число набуває значень від одиниці до нескінченості: n = 1,2,3…∞. Кожному значенню n відповідає певний запас енергії електрона Е. Із збільшенням значення n збільшується запас енергії електрона та відстань електрона від ядра, послаблюється зв’язок електрона з ядром. Якщо n=1, то це означає, що електрон знаходиться на першому енергетичному рівні; якщо n=2, то це означає, що електрон знаходиться на другому енергетичному рівні; n=3, то – на третьому рівні тощо:

n = 1, 2, 3, 4, …….. 

Е₁ < E₂ < E₃ < E₄

І ІІ ІІІ ІV

енергетичні рівні

Орбітальне квантове число ℓ характеризує енергію електрона на певному енергетичному підрівні у межах одного енергетичного рівня та форму електронної хмари. Орбітальне квантове число набуває значень від 0 через кожну одиницю до (n-1), але максимальне значення ℓ не перевищує 3 для заповнених електронами енергетичних рівнів атомів відомих хімічних елементів: ℓ = 0  (n-1); ℓ _max ≤ 3.

Із збільшенням значення ℓ, при однаковому значенні n, збільшується енергія електрона у межах енергетичного рівня, тобто енергетичний рівень розщеплюється на підрівні.

Винятком є перший енергетичний рівень, для якого n=1, а ℓ=0. Це свідчить про те, що перший енергетичний рівень складається тільки з одного підрівня, який називається 1s-підрівнем. Число перед буквою вказує на те, що підрівень належить першому енергетичному рівню.

Якщо n=2, то ℓ=0 та 1. Орбітальне квантове число набуває двох значень, що свідчить про те, що другий енергетичний рівень розщеплюється на два підрівні: 2s- підрівень (ℓ=0) та 2р-підрівень (ℓ=1).

Якщо n=3, то ℓ набуває трьох значень: 0,1,2. Отже, третій енергетичний рівень розщеплюється на три підрівні: 3s- підрівень (ℓ=0), 3р-підрівень (ℓ=1) та 3d-підрівень (ℓ=2).

Четвертий енергетичний рівень (n=4) та всі подальші енергетичні рівні мають чотири підрівні: s-підрівень (ℓ=0), р-підрівень (ℓ=1), d-підрівень (ℓ=2) та f-підрівень (ℓ=3).

Отже, енергія електрона в атомі залежить від значення n і меншою мірою від значення ℓ.

Електрони, які перебувають на s-підрівні, називаються s-електронами, а на р-, d-, та f-підрівнях – відповідно р-, d-, та f-електронами. Частина простору, де ймовірність перебування s-електронів найбільша, тобто s-електронна хмара має форму кулі; р-електронна хмара має форму гантелі або об’ємної вісімки.

Магнітне квантове число m_ℓ характеризує можливі орієнтації електронної хмари певної форми у просторі. Магнітне квантове число набуває значень від – ℓ через кожну одиницю до + ℓ:

m_ℓ = - ℓ …0…+ ℓ

Якщо ℓ=0 (s-підрівень), то m_ℓ теж дорівнює 0. Одному значеню m_ℓ відповідає один спосіб орієнтації s-електронної хмари у просторі.

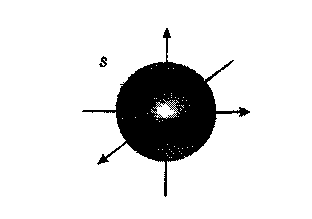
Наведений набір квантових чисел: будь-яке значення n, ℓ=0 та m_ℓ=0 – вказує на те, що s-підрівень будь-якого енергетичного рівня містить тільки одну атомну орбіталь, яка називається s-атомною орбіталлю (s-АО).

Якщо ℓ =1 (р-підрівень), то m_ℓ= -1, 0,+1. Три значення m_ℓ свідчать про три способи орієнтації р-електронної хмари у просторі, а саме – вздовж осей x, y, z:

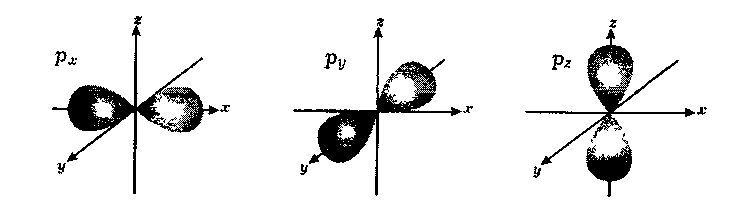
Таким чином, р-підрівень складається з трьох атомних орбіталей, які позначаються так: р_х-, р_у-, р_z-АО.

Якщо ℓ=2 (d-підрівень), m_ℓ = -2, -1, 0, +1, +2. Отже, d-підрівень складається з п‘яти d-атомних орбіталей, а f-підрівень (ℓ =3, m_ℓ= -3, -2, -1, 0, +1, +2, +3) – з сьоми f-атомних орбіталей.

Енергія електрона не залежить від способу орієнтації його електронної хмари у просторі, отже, електрони, що розміщені на атомних орбіталях одного і того ж підрівня, мають однакову енергію.

Значення трьох квантових чисел є повною характеристикою атомної орбіталі.

Але для характеристики стану електронів в атомі недостатньо значень трьох квантових чисел. Особливості атомних спектрів можна пояснити, якщо припустити наявність у електронів власного моменту кількості руху. Напрямок у просторі вектора власного моменту кількості руху електрона характеризується спіновим квантовим числом m_s, яке набуває таких значень: +½, -½. Два значення m_s вказують на два взаємно протилежні напрямки цього вектора у просторі, які позначають стрілками:

m_s= + ½; ↑ m_s= - ½. ↓

Значення чотирьох квантових чисел n,ℓ,m_ℓ,m_s повністю характеризують квантовий стан електрона в атомі.

Хімічні властивості елементів залежать від структури електронної оболонки їх атомів, тобто від розподілу електронів по атомних орбіталях енергетичних рівнів та підрівнів, який відбувається за трьома правилами: за принципом Паулі, за правилом Хунда та правилом Клечковського.

Принцип Паулі. ”В атомі не можуть перебувати навіть два електрони з однаковим набором квантових чисел”.

Приклад. Охарактеризуйте квантовий стан електронів, які знаходяться на 5s-атомній орбіталі.

Розв’язання. Оскільки електрони розміщені на п’ятому енергетичному рівні, то n=5. Для s – підрівня ℓ=0 та m_ℓ=0. Спінове квантове число електронів становить лише +½ або -½. Значення квантових чисел для двох 5s-електронів наведені в таблиці:

Електрон	n	ℓ	mℓ	ms
Перший	5	0	0	+½
Другий	5	0	0	-½

Третій електрон мав би такий же набір квантових чисел, як і один з наведених в таблиці. Отже, за принципом Паулі на одній атомній орбіталі не може перебувати більше двох електронів. Якщо на орбіталі знаходиться один електрон, то він називається неспареним, а якщо два, то це – спарені електрони з антипаралельними спінами, тобто із значеннями спінового квантового числа +½ та –½.

Принцип Паулі обмежує число електронів на енергетичних підрівнях та рівнях: максимальне число електронів на першому енергетичному рівні становить два (1s²), на другому – вісім (2s²2р⁶), на третьому – 18 (3s²3p⁶3d¹⁰), на четвертому ( і на подальших ) – 32 (4s²4p⁶4d¹⁰4f¹⁴).

Правило Хунда визначає порядок розміщення електронів на атомних орбіталях в межах одного підрівня:

”Атомні орбіталі одного і того ж підрівня заповнюються електронами так, щоб модуль суми спінових квантових чисел був найбільшим”. Винятком є лише s-підрівень, на якому містяться не більше двох електронів з антипаралельними спінами: s^↑↓.

Приклад. Вкажіть, який спосіб розміщення трьох електронів на р-підрівні є вірним:

а) р_х^↑р_у^↑р_z^↓_; б) р_х^↑↓р_у^↑р_z; в) р_х^↑р_у^↑р_z^↑

Розв’язання. Розрахуємо модуль суми спінових квантових чисел у кожному випадку:

а) , б) в) .

Отже, електрони розміщуються на р-підрівні за варіантом в), для якого модуль суми спінових квантових чисел є найбільшим.

Правило Клечковського визначає порядок заповнення електронами атомних орбіталей різних підрівнів і є відображенням принципа найменшої енергії, за яким електрон в атомі займає атомну орбіталь того підрівня, де його енергія буде найнижчою. Оскільки енергію електрона в атомі характеризують головне та орбітальне квантові числа, то сума їх значень дозволяє порівнювати енергію електрона на тому чи іншому підрівні: чим менша сума (n+ℓ), тим нижча енергія електрона на підрівні.

Правило Клечковського складається з двох частин:

1) атомні орбіталі різних підрівнів заповнюються електронами у порядку збільшення суми значень головного та орбітального квантових чисел (n+ℓ),

2) якщо сума (n+ℓ) для різних підрівнів однакова, то спочатку заповнюються електронами атомні орбіталі підрівня з меншим значенням n. Це пояснюється тим, що енергія електрона більшою мірою залежить від значення n, ніж від значення ℓ.

Розрахуємо суму (n+ℓ) для деяких підрівнів в атомі та вкажемо стрілкою послідовність їх заповнення електронами:

1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p

n+ℓ

1s2s2p3s3p4s3d4p5s4d5p6s4f5d6p

Отже, енергія електрона на 4s-підрівні нижча за енергію електрона на 3d-підрівні. Тому, не зважаючи на те, що третій енергетичний рівень складається з трьох підрівнів, після заповнення 3s- та 3p-підрівнів наступним заповнюється електронами не 3d-, а 4s-підрівень. Такий же порядок заповнення підрівнів електронами відбувається і на інших енергетичних рівнях.

Висновки:

1. Перший енергетичний рівень має тільки один підрівень (1s-підрівень). Другий енергетичний рівень розщеплюється на два підрівні (2s- та 2p-підрівні), третій – на три підрівні (3s-, 3p- та 3d-підрівні), четвертий – на чотири підрівні (4s-, 4p-, 4d- та 4f-підрівні). На всіх подальших енергетичних рівнях атомів відомих хімічних елементів електрони заповнюють теж чотири підрівні.

2. s-Підрівень складається з однієї атомної орбіталі (s-AO), p-підрівень – з трьох атомних орбіталей ( p_x–, p_y–, p_z– AO), d-підрівень – з п‘яти d- атомних орбіталей, а f-підрівень – з сьоми f-атомних отбіталей.

3. Принцип Паулі обмежує число електронів на кожному енергетичному рівні: максимальне число електронів на першому енергетичному рівні становить два (1s²), на другому – вісім (2s²2p⁶), на третьому – вісімнадцять (3s²3p⁶3d¹⁰), на четвертому (та подальших рівнях) – тридцять два (4s²4p⁶4d¹⁰4f¹⁴).

4. Правило Хунда визначає порядок заповнення електронами атомних орбіталей в межах одного p-, d- та f-підрівня.

5. Правило Клечковського визначає порядок заповнення електронами атомних орбіталей різних підрівнів.

Розміщення електронів в атомі на атомних орбіталях енергетичних рівнів та підрівнів зображують у вигляді електронної конфігурації (електронної формули).