Задание 4

В качестве объекта управления примем быстроходный патрульный катер, управляемый с помощью вертикальных рулей направления и специальных щитков – интерцепторов, выдвигающихся из днища судна и создающих управляющий момент по крену.

Б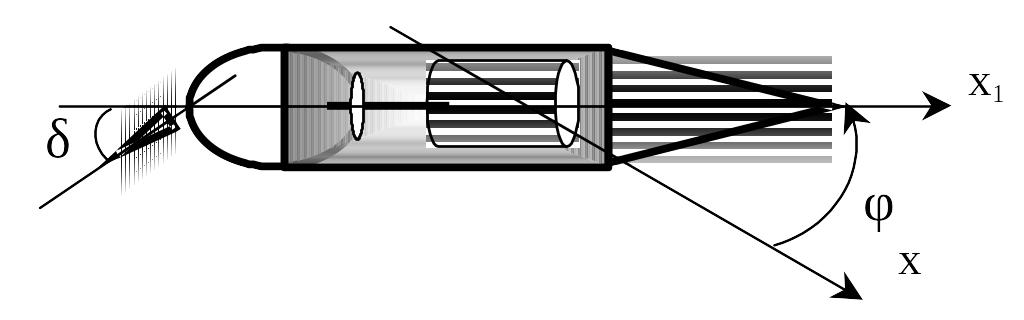 удем рассматривать процесс стабилизации катера в боковом движении по рысканию и крену на постоянной скорости хода м/с с помощью отклонения рулей направления на угол и с помощью разностного выдвига внешних секций кормовых интерцепторов (рис. 2.5.4).

Рис. 2.5.4.

Будем описывать процесс стабилизации с помощью следующей системы линейных дифференциальных уравнений:

,

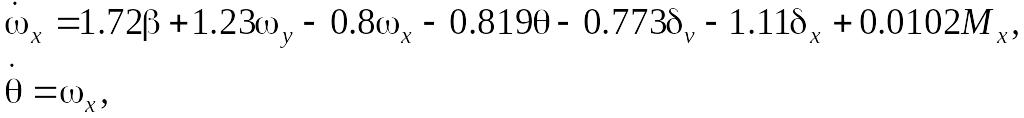
Здесь – угол дрейфа, – угловая скорость по рысканию, – угловая скорость по крену, – угол рыскания, – угол крена; , и – внешние возмущения.

Необходимо выполнить следующие действия:

1. Сформировать LTI-объект, соответствующий данной модели. Входом считать вектор с компонентами , , , и . Выходом – вектор с компонентами и .

2. Найти передаточные функции от входа к выходу и от входа к выходу . Построить диаграммы Боде для этих функций и найти частоты, на которой их амплитудные части достигают локального максимума.

Задание 5

Р ассмотрим движение корабля в горизонтальной плоскости (рис. 2.5.5), который управляется с помощью вертикального руля направления. Будем учитывать инерционность привода рулей. В качестве математической модели процесса стабилизации на заданном курсе примем систему обыкновенных линейных дифференциальных уравнений вида (2.5.2). Здесь – угол дрейфа, – угловая скорость по рысканию, – угол рыскания.

Рис. 2.5.5.

(2.5.2)

Здесь через обозначено отклонение руля, а через – управляющий сигнал. Примем следующие величины числовых значений параметров модели (2.5.2), которые соответствуют кораблю водоизмещением 3000 т, идущим с постоянной скоростью 10 м/с: , , , , , .

Необходимо выполнить следующие действия:

1. Сформировать управление в виде

. (2.5.3)

Аналитически (формулой) найти такую величину постоянного командного сигнала , который обеспечит для замкнутой системы (2.5.1), (2.5.2) равенство , где – заданное число.

2. Задать коэффициенты закона управления , , , и сформировать LTI-объект, соответствующий математической модели замкнутой системы, причем его входом считать переменную , а выходом – переменную .

3. Найти передаточную функцию полученного объекта от входа к выходу.

Задание 6

В качестве объекта управления примем вертолет, движущийся в вертикальной плоскости. Управление движением осуществляется с помощью наклона плоскости несущего винта на угол .

Д ля динамических параметров движения примем следующие обозначения: – угол тангажа, – перемещение в горизонтальном направлении. Задача системы стабилизации – удержать машину в заданном положении при воздействии внешних возмущений.

Рис. 2.5.6.

В качестве математической модели процесса стабилизации примем следующую систему обыкновенных дифференциальных уравнений:

(2.5.4)

где , , , , , ,

. При этом измеряется в радианах, а – в метрах.

Необходимо выполнить следующие действия:

1. Сформировать LTI-объект, соответствующий данной модели. Входом считать переменную , а выходом – вектор с компонентами и .

2. Найти передаточные функции от входа к выходным переменным. Построить диаграммы Боде для этих функций.

69