Чисельне інтегрування

1)Задача інтегрування неперервної функції легко розв'язується аналітично, якщо відома її первісна F (x). Визначений інтеграл від цієї функції може бути обчислений по формулі Ньютона - Лейбніца: , де F(x) =f(x).

Проте у багатьох випадках первісна F(x) не може бути виражена за допомогою елементарних функцій або є дуже складною. Тому обчислення визначеного інтеграла по формулі Ньютона-Лейбніца може бути нездійсненним або важким.

2)Наприклад, - інтеграл, що не береться в елементарних функціях.

Наближене обчислення інтегралів , полягає заміні визначеного інтеграла скінечною сумою , де С_k числові коефіцієнти і x_k - деякі точки, k=0, 1,…,n.

Означення 1. Наближена рівність називається квадратурною формулою. Точки x_k називаються вузлами квадратурної формули. Різниця називається похибкою квадратурної формули.

Слід помітити, що в більш загальному означенні квадратурної формули в суму можуть входити не тільки значення функції, але і значення першої похідної.

Похибка залежить від функції f, відрізка інтегрування, від розташування вузлів і вибору коефіцієнтів квадратурної формули. Вузли квадратурної формули можуть належати до відрізка інтегрування, а можуть і не належати. Наближене інтегрування може бути виконане з будь-якою точністю.

Означення 2. Для зниження похибки чисельного інтегрування відрізок [а,b] розібємо на сукупність малих відрізків [x_i-1,x_i] , таких, що . Представимо інтеграл у вигляді суми інтегралів по часткових відрізках: .

Така формула чисельного інтегрування називається складеною.

Формула трапецій

1)Замінимо функцію f(х) на відрізку [x_i-1,x_i] інтерполяційним поліномом Лагранжа першого степеня. Позначимо y_i=f(x_i), y_i-1=f(x_i-1), h= x_i-x_i-1. Інтерполяційний поліном Лагранжа першого степеня для двох точок:P₁(x)=y_i-1L₁(x)+ y_iL₂(x).

Для L₁(x)=(x-x_i)/(x_i-1-x_i)=(x_i-x)/h, L₂(x)=(x-x_i-1)/(x_i-x_i-1)=(x-x_i-1)/h.

Похибка: R(x)=(x-x_i-1)(x-x_i)*f"(t)/2, де x_i-1≤ t ≤ x_i .

Тоді f(х)=P₁(x)+R(x)= [y_i-1(x_i-x)+ y_i (x-x_i-1)]/h+f ()(x-x_i)(x-x_i-1)/2 , де точка [x_i-1,x_i] .

Обчислимо інтеграл I₁:

Обчислимо інтеграл I₂:

Остатоточно, .

Оцінимо тепер інтеграл I₃.

Припустимо, що модуль другої похідної від функції f обмежений на відрізку [а,b]: f (x)<M , при всіх х, що належать відрізку [а,b].

Тепер можна оцінити інтеграл I₃ (похибку):

 I₃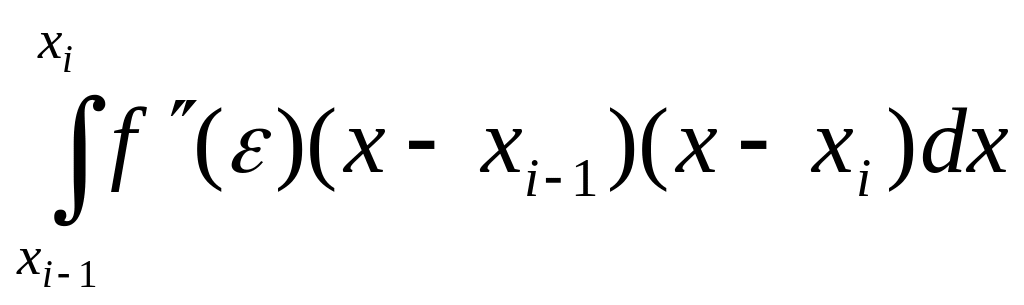= /2< , де або

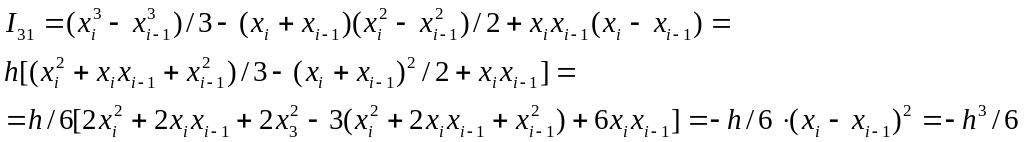
Отже,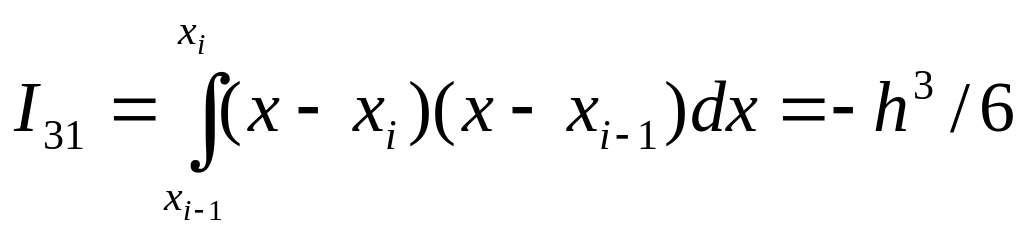

Таким чином .

Складена формула трапецій

Якщо застосувати цю формулу до всього відрізка [а,b], при умові що відрізок розбитий на N однакових частин, h=(b-а)/N, то одержимо складену формулу трапецій:

Похибка складеної формули трапецій P не перевищує суми похибок по кожному відрізку:

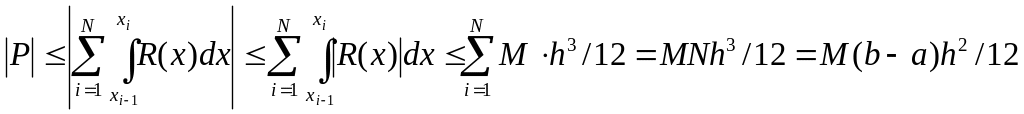
Останнє витікає з того, що h=(b-а) /N, а Nh=b-a.

Цю ж формулу можна записати і по іншому:

Таким чином, формула трапецій має, другий порядок точності. Ця формула точна для поліномів не вище першого степеня.

Приклад 1. Для інтеграла при числі відрізків N=10 обчислити похибку чисельного інтегрування за методом трапецій. За формулою

похибка буде рівна 10^-2/12 або близько 0.0008, оскільки в даному випадку M<1, h=10^-1.

Приклад 2.Тепер вирішимо обернену задачу, найбільш важливу для практики. Потрібно обчислити інтеграл з заданою точністью для рівномірного розбиття відрізку. Яким потрібно взяти N? Для цього розвяжемо рівняння відносно N. Для N отримаємо нерівність: . Нехай , тоді . Якщо взяти відрізок , то в цьому випадку .

Блок-схема складеної формули трапецій на рис. 1. В якості приклада розглянемо обчислення інтеграла . Як відомо, точне значення інтеграла рівне , при значення інеграла рівне ,похибка методу трапецій рівна . При , , .

Труднощі запропонованого методу:

1)Метод трапецій має невелику точність;

2)Важко оцінити значення M, тобто модуля другої похідної від функції f на відрізку [а,b];

3)Значення N практично завжди буде завищеним.