Тема 10. Производные функций
Найти производные первого порядка явно заданных функций:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
Найти производные указанного порядка явно заданных функций:
23.
24.
25.
26.
Найти
функций, заданных неявно:
27.
.
28.
.
29.
.
30.
.
31.
.
32.
.
Найти
для функций, заданных параметрически:
33.
34.
35.
36.
37.
38.
Ответы к теме 10
1. 
.
2. 
.
3. 
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
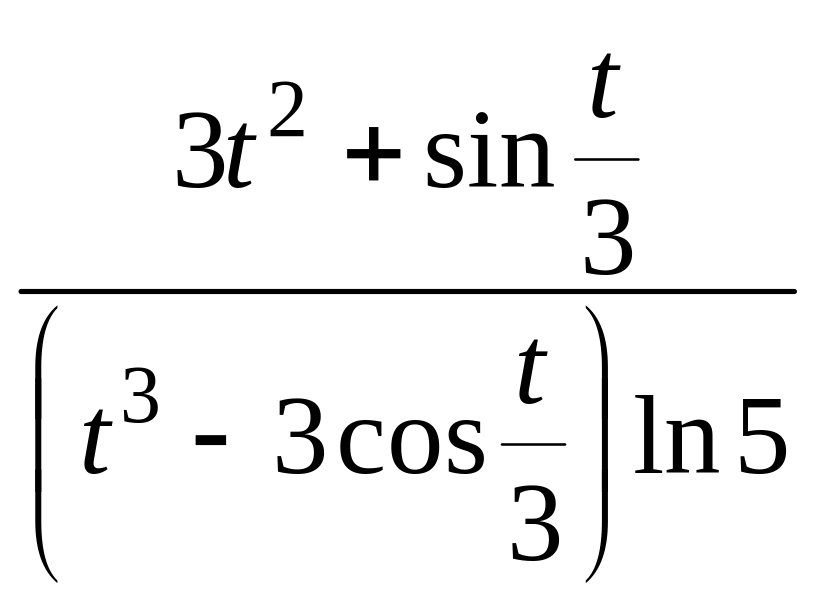15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25. 24.
26. 27e.
27.
.
28.
.
29.
.
30.
.
31.
.
32.
.
33.
.
34.
.
35.
.
36.
.
37.
.
38.
.
Тема 11. Правило Лопиталя для вычисления пределов функций
Вычислить пределы, пользуясь правилом Лопиталя:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
Ответы к теме 11
1. 7/2; 2. 5; 3. –1/3; 4. 7/3; 5. 2; 6. 3; 7. 1/2; 8. 1/2; 9. 2/3; 10. 2; 11. 1; 12. e–2; 13. 1; 14. e2.
Тема 12. Исследование функций. Построение графиков функций
1. Найти интервалы возрастания и убывания функций:
а)
; б)
;
в)
; г)
.
2. Исследовать функции на экстремум:
а)
; б)
;
в)
; г)
.
3. Найти наибольшее и наименьшее значения функций на заданных промежутках:
а)
; б)
;
в)
; г)
.
4. Найти интервалы выпуклости, вогнутости и точки перегиба графиков следующих функций:
а)
; б)
;
в)
; г)
.
5. Найти асимптоты графиков функций:
а)
; б)
;
в)
; г)
.
6. Исследуйте функции и постройте их графики:
а)
; б)
;
в)
; г)
.
Ответы к теме 12
1. а)
– возрастает;
– убывает;
б)
– возрастает;
– убывает;
в)
–
убывает;
– возрастает;
г)
– возрастает;
– убывает.
2. а)
– локальный максимум,
– локальный минимум,
;
б)
– локальный минимум,
;
в)
– локальный минимум,
;
– локальный максимум,
;
г)
– локальный максимум,
– локальный минимум,
.
3. а)
;
б)
;
в)
;
г)
.
4. а)
– функция выпукла; 
– функция вогнута; 
– точки перегиба;
б)
– функция выпукла; 
– функция вогнута; 
– точки перегиба;
в)
– функция вогнута; точек перегиба нет;
г)
– функция выпукла; 
– функция вогнута; 
– точка перегиба.
5. а)
; б)
;
в)
; г)
(правая),
(левая).
Контрольная работа № 1
Задание 1. а) Проверить невырожденность системы линейных уравнений и решить ее по формулам Крамера и матричным способом.
б) Исследовать систему на совместность и в случае совместности решить ее, используя метод Гаусса.
1.1. |
а) |
|
б) |
|
1.2. |
а) |
|
б) |
|
1.3. |
а) |
|
б) |
|
1.4. |
а) |
|
б) |
|
1.5. |
а) |
|
б) |
|
1.6. |
а) |
|
б) |
|
1.7. |
а) |
|
б) |
|
1.8. |
а) |
|
б) |
|
1.9. |
а) |
|
б) |
|
1.10. |
а) |
|
б) |
|
1.11. |
а) |
|
б) |
|
1.12. |
а) |
|
б) |
|
1.13. |
а) |
|
б) |
|
1.14. |
а) |
|
б) |
|
1.15. |
а) |
|
б) |
|
1.16. |
а) |
|
б) |
|
1.17. |
а) |
|
б) |
|
1.18. |
а) |
|
б) |
|
1.19. |
а) |
|
б) |
|
1.20. |
а) |
|
б) |
|
1.21. |
а) |
|
б) |
|
1.22. |
а) |
|
б) |
|
1.23. |
а) |
|
б) |
|
1.24. |
а) |
|
б) |
|
1.25. |
а) |
|
б) |
|
1.26. |
а) |
|
б) |
|
1.27. |
а) |
|
б) |
|
1.28. |
а) |
|
б) |
|
1.29. |
а) |
|
б) |
|
1.30. |
а) |
|
б) |
|
Задание 2. Заданы
координаты точек А,
В,
С.
Требуется найти: 1)
;
2) площадь треугольника с вершинами
в
точках А, В, С.
2.1. А(7,1,4), В(9,–2,0), С(0,3,–3).
2.2. А(3,1,4), В(–3,–1,0), С(2,1,–3).
2.3. А(2,1,0), В(3,–1,–4), С(0,2,–2).
2.4. А(3,–1,–1), В(3,1,4), С(1,0,5).
2.5. А(2,1,–1), В(7,–1,3), С(0,3,3).
2.6. А(2,–3,7), В(–3,–1,5), С(9,0,1).
2.7. А(7,–3,4), В(3,2,–1), С(4,1,1).
2.8. А(1,1,0), В(2,1,–4), С(0,1,0).
2.9. А(1,–1,4), В(2,3,–4), С(1,0,–5).
2.10. А(2,–4,7), В(8,1,0), С(–1,–3,0).
2.11. А(1,–1,0), В(0,1,7), С(–1,–2,–3).
2.12. А(0,9,–3), В(1,3,4), С(0,2,–5).
2.13. А(1,–1,3), В(2,–2,4), С(1,0,1).
2.14. А(2,–2,–3), В(–1,–4,7), С(0,4,–3).
2.15. А(1,0,0), В(–3,1,–1), С(1,–2,–3).
2.16. А(1,3,7), В(7,3,–5), С(–1,–4,0).
2.17. А(1,–1,1), В(0,1,0), С(1,4,–5).
2.18. А(2,–2,3), В(1,–1,4), С(0,1,–1).
2.19. А(2,0,–1), В(1,–1,1), С(0,1,7).
2.20. А(1,–1,3), В(2,1,–4), С(0,1,0).
2.21. А(1,–2,2), В(2,0,1), С(1,4,–7).
2.22. А(1,2,–3), В(2,–1,4), С(2,3,–4).
2.23. А(7,9,–3), В(1,0,–1), С(0,3,0).
2.24. А(1,–2,0), В(2,4,–1), С(7,1,0).
2.25. А(3,–1,4), В(–4,2,3), С(0,1,–1).
2.26. А(6,–3,0), В(3,0,1), С(2,–4,3).
2.27. А(4,5,–1), В(6,–4,2), С(0,3,–1).
2.28. А(3,–1,2), В(3,6,–4), С(0,1,–1).
2.29. А(1,1,–1), В(3,4,0), С(0,5,–2).
2.30. А(1,0,2), В(3,4,7), С(5,–1,1).
Задание 3. Найти
угол (в градусах) между прямой
и плоскостью, проходящей через точки
.
3.1. |
M1(1,–3,4), |
M2(0,–2,–1), |
M3(1,1,–1). |
3.2. |
M1(1,1,4), |
M2(–2,1,1), |
M3(1,3,6). |
3.3. |
M1(1,2,–1), |
M2(–1,0,4), |
M3(–2,–1,1). |
3.4. |
M1(1,2,3), |
M2(4,–1,–2), |
M3(4,0,3). |
3.5. |
M1(1,3,–1), |
M2(–3,1,–9), |
M3(1,0,–7). |
3.6. |
M1(1,–2,–1/2), |
M2(2,1,3), |
M3(0,–1,–1). |
3.7. |
M1(1,1,4), |
M2(2,–1,0), |
M3(3,2,1). |
3.8. |
M1(–13,3,2), |
M2(–3,–2,–4), |
M3(0,0,–3). |
3.9. |
M1(1,–1,–3), |
M2(0,6,1), |
M3(2,2,–2). |
3.10. |
M1(2,3,–10), |
M2(1,–1,–9), |
M3(0,–1,–4). |
3.11. |
M1(1,1,4), |
M2(2,0,2), |
M3(0,3,3). |
3.12. |
M1(2,1,–3), |
M2(1,1,0), |
M3(–1,2,7). |
3.13. |
M1(1,0,1), |
M2(0,0,2), |
M3(1,1,1). |
3.14. |
M1(–5,–1,1), |
M2(–2,0,1), |
M3(–1,1,0). |
3.15. |
M1(2,1,3), |
M2(0,0,4), |
M3(1,1,1). |
3.16. |
M1(2,3,1), |
M2(4,–4,–2), |
M3(1,0,0). |
3.17. |
M1(–1,0,1), |
M2(3,–2,–1), |
M3(–4,–1,2). |
3.18. |
M1(2,–2,9), |
M2(–2,0,1), |
M3(–4,1,3). |
3.19. |
M1(1,2,–1), |
M2(2,3,–10), |
M3(0,4,1). |
3.20. |
M1(1,–2,1), |
M2(0,–1,2), |
M3(2,–1,–1). |
3.21. |
M1(1,–2,–5), |
M2(2,3,2), |
M3(–1,0,5). |
3.22. |
M1(1,3,4), |
M2(0,1,2), |
M3(2,5,0). |
3.23. |
M1(1,–1,0), |
M2(–3,–4,1), |
M3(–1,–1,2). |
3.24. |
M1(–1,2,0), |
M2(6,3,1), |
M3(–15,0,2). |
3.25. |
M1(1,2,3), |
M2(2,4,1), |
M3(2,0,–3). |
3.26. |
M1(–1,1,0), |
M2(3,–4,5), |
M3(–2,0,2). |
3.27. |
M1(2,–3,5), |
M2(1,–2,12), |
M3(4,–1,7). |
3.28. |
M1(3,–1,2), |
M2(4,–1,–1), |
M3(2,0,2). |
3.29. |
M1(1,3,1), |
M2(4,0,7), |
M3(–2,1,2). |
3.30. |
M1(1,–1,1), |
M2(5,4,–2), |
M3(–1,–2,2). |
Задание 4. Упростить уравнение кривой и изобразить ее на рисунке
