
- •8. Задачи для самостоятельного решения
- •Тема 1. Матрицы. Определители
- •Ответы к теме 1
- •Тема 2. Системы линейных алгебраических уравнений
- •Ответы к теме 2
- •Тема 3. Векторы
- •Ответы к теме 3
- •Тема 4. Прямая на плоскости
- •Ответы к теме 4
- •Тема 5. Плоскость и прямая в пространстве
- •Ответы к теме 5
- •Тема 6. Кривые второго порядка
- •Ответы к теме 6
- •Тема 7. Поверхности второго порядка
- •Ответы к теме 7
- •Тема 8. Пределы функций
- •Ответы к теме 8
- •Тема 9. Непрерывность функций. Точки разрыва и их классификация
- •Ответы к теме 9
- •Тема 10. Производные функций
- •Ответы к теме 10
- •Тема 11. Правило Лопиталя для вычисления пределов функций
- •Ответы к теме 11
- •Тема 12. Исследование функций. Построение графиков функций
- •Ответы к теме 12
- •Контрольная работа № 1
- •Задание 5. Найти пределы функций:
- •Литература
- •Математика
- •Часть 1
8. Задачи для самостоятельного решения
Тема 1. Матрицы. Определители
1. Найти матрицу, транспонированную матрице А:
а)
 ; б)
; б)
 ; в)
; в)
![]() .
.
2.
Даны матрицы
 .
.
Найти а) 2А; б)
![]() ; в)
; в)
![]() .
.
3.
Найти 3A+2E,
если
 ,
E
– единичная матрица третьего порядка.
,
E
– единичная матрица третьего порядка.
4. Вычислить определители второго порядка:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
![]() .
.
5. Вычислить определители третьего порядка различными способами:
а)
 ; б)
; б)
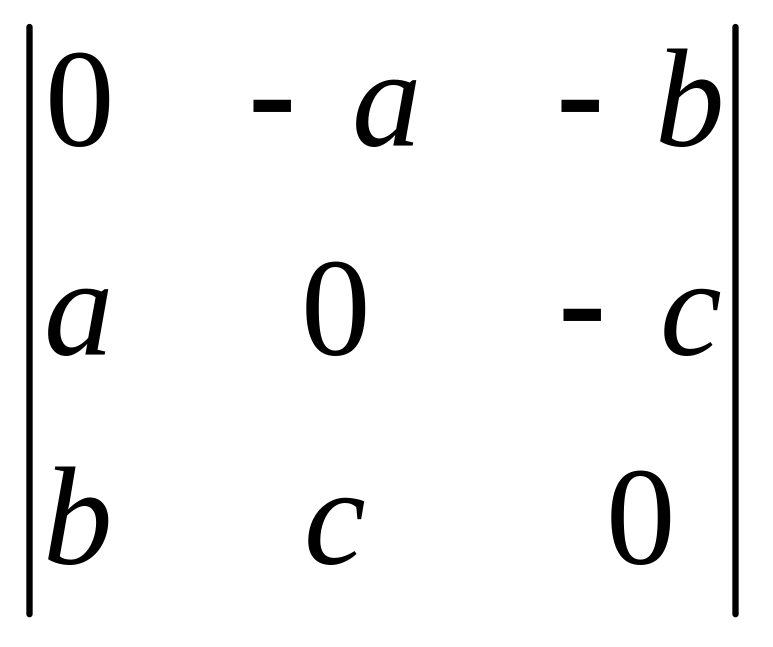 ; в)
; в)
 ;
;
г)
 ; д)
; д)
 ; е)
; е)
 .
.
6. Найти обратную матрицу:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
 ;
г)
;
г)
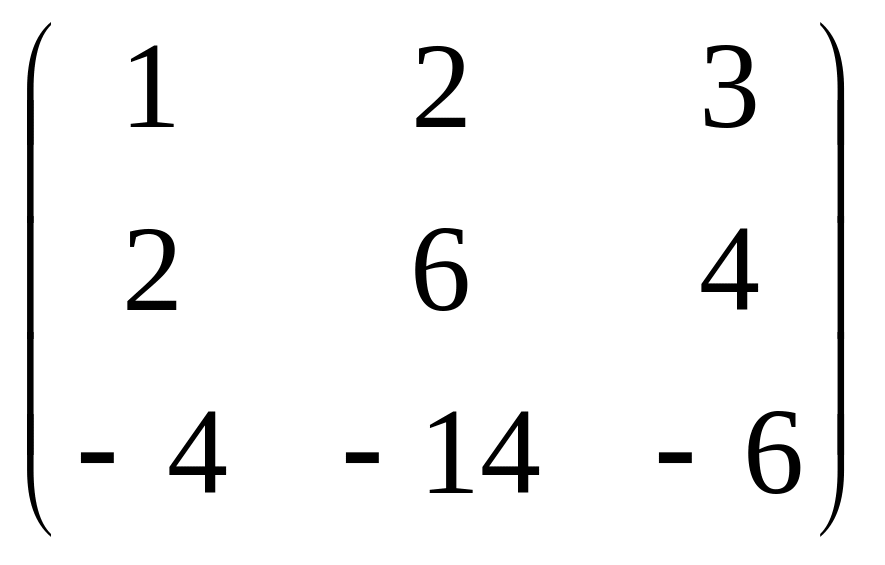 .
.
7.
Решить уравнение
 .
.
8.
Построить график функции
 .
.
9. Решить матричные уравнения:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
10. Найти ранг матрицы:
а)
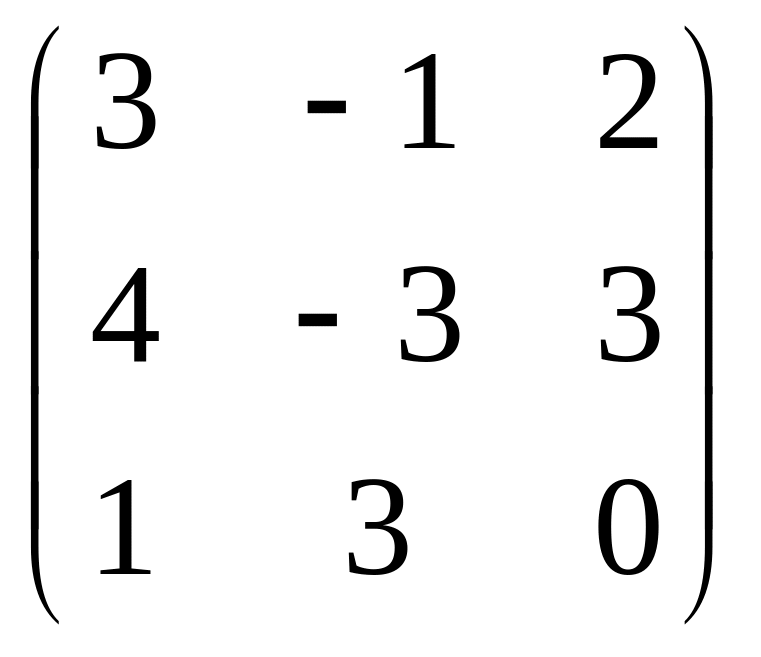 ; б)
; б)
 .
.
Ответы к теме 1
1.
а)
 ; б)
; б)
![]() ; в)
; в)
 .
.
2.
 .
.
3.
 . 4.
а) 13; б)
. 4.
а) 13; б)
![]() ; в)
; в)
![]() ;
г) 2a; д)
;
г) 2a; д)
![]() .
.
5.
а) 78; б) 0; в)
![]() ; г)
78; д) 100; е)
– 6.
; г)
78; д) 100; е)
– 6.
6.
а)
![]() ; б)
; б)
![]() ; в)
; в)
 ;
;
г) не существует. 7.
![]() . 8.
Прямая
. 8.
Прямая
![]() .
.
9.
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() . 10.
а) 2; б) 2.
. 10.
а) 2; б) 2.
Тема 2. Системы линейных алгебраических уравнений
1. Убедиться, что система является невырожденной, и решить ее по формулам Крамера и матричным способом:
а)
 б)
б)
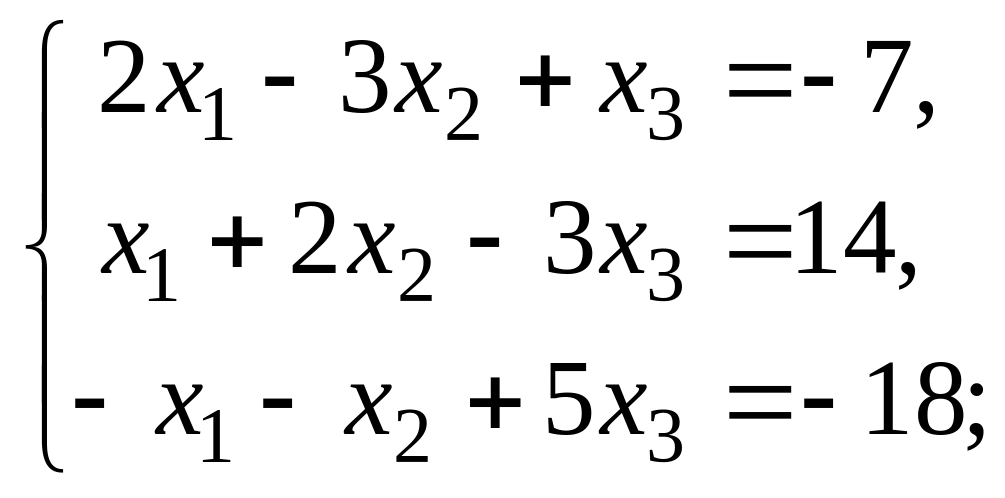
в)

2. Решить системы методом Гаусса:
а)
 б)
б)

в)
 г)
г)

Ответы к теме 2
1. а) (–2;2;1); б) (1;2;–3); в) (–3;3;0).
2.
а)
![]() ; б)
несовместна;
; б)
несовместна;
в)
![]() ; г)
(–2;1;2).
; г)
(–2;1;2).
Тема 3. Векторы
1.
Как должны быть связаны векторы
![]() и
и
![]() ,
чтобы выполнялись соотношения:
,
чтобы выполнялись соотношения:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() .
.
2. Даны
точки
![]() .
Докажите, что ABCD
– равнобедренная трапеция.
.
Докажите, что ABCD
– равнобедренная трапеция.
3.
При каких α и
векторы
![]() и
и
![]() ортогональны, а векторы
и
ортогональны, а векторы
и
![]() коллинеарны?
коллинеарны?
4. Дан
треугольник с вершинами в точках
![]()
![]() .
Найти: а) внутренний угол при вершине
С;
б) пло-
щадь треугольника АВС;
в) длину высоты, опущенной из вершины С
на АВ.
.
Найти: а) внутренний угол при вершине
С;
б) пло-
щадь треугольника АВС;
в) длину высоты, опущенной из вершины С
на АВ.
5. Даны
векторы
![]() ,
,
![]() ,
,
![]() .
Найти
.
Найти
![]() .
.
6. Какую
работу производит сила
![]() ,
когда точка ее приложения, двигаясь
прямолинейно, перемещается из точки
,
когда точка ее приложения, двигаясь
прямолинейно, перемещается из точки
![]() в точку
в точку
![]() ?
?
7. Найдите
какой-либо ненулевой вектор
![]() ,
перпендикулярный векторам
,
перпендикулярный векторам
![]() и
и
![]() .
.
8. Вычислите
синус угла, образованного векторами
![]() и
и
![]() .
.
9. Выясните, компланарны ли векторы:
а)
![]() ,
, ![]() ,
, ![]() ;
;
б)
![]() ,
, ![]() ,
, ![]()
10. Вычислите
объем тетраэдра ABCD
и длину высоты, опущенную из точки D
на основание ABC,
если известны координаты его вершин
![]() .
.
11. Сила
![]() приложена к точке
приложена к точке
![]() .
Определите величину и направляющие
косинусы момента силы относительно
начала координат.
.
Определите величину и направляющие
косинусы момента силы относительно
начала координат.
12. Даны
три силы
![]() ,
приложенные к точке
,
приложенные к точке
![]() .
Определите величину и направляющие
косинусы момента равнодействующей силы
относительно точки
.
Определите величину и направляющие
косинусы момента равнодействующей силы
относительно точки
![]() .
.
Ответы к теме 3
1.
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)![]() .
.
3.
а)
![]() ;
б)
;
б)
![]() . 4.
а)
. 4.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() . 5.
5. 6.
20. 7.
. 5.
5. 6.
20. 7.
![]() . 8.
. 8.
![]() .
.
9.
а) да; б) нет. 10. ![]() .
.
11.
![]() .
.
12.
![]() .
.
Тема 4. Прямая на плоскости
1. Написать
уравнение прямой, проходящей через
точки
![]()
![]() ,
и найти точки ее пересечения с осями
координат.
,
и найти точки ее пересечения с осями
координат.
2. Составить
уравнение прямой, проходящей через
точку
![]() ,
являющуюся основанием перпендикуляра,
опущенного из начала координат на эту
прямую.
,
являющуюся основанием перпендикуляра,
опущенного из начала координат на эту
прямую.
3.
При каком значении A
прямая
![]() образует с осью Ox
угол
образует с осью Ox
угол
![]() ?
?
4. Даны
вершины треугольника
![]() .
Найти: а) уравнение стороны AB;
б) уравнение медианы, проведенной из
вершины C;
в) уравнение высоты, проведенной из
вершины C.
.
Найти: а) уравнение стороны AB;
б) уравнение медианы, проведенной из
вершины C;
в) уравнение высоты, проведенной из
вершины C.
5. Написать уравнение прямой, параллельной биссектрисе второго координатного угла и отсекающей на оси Oy отрезок, равный 3.
6.
Найдите уравнение прямой, проходящей
через точку
![]() :
а) параллельно прямой
:
а) параллельно прямой
![]() ;
б) перпендикулярно прямой
;
б) перпендикулярно прямой
![]() .
.
7. Каково взаимное расположение двух прямых, угловые коэффициенты которых равны –2,5 и –0,4.
8.
Найдите расстояние от точки
![]() до прямой:
до прямой:
а)
![]() б)
б)
![]()
9. Какие прямые данной пары пересекаются, параллельны или совпадают? Если прямые пересекаются, найдите координаты точки их пересечения:
а)
![]() и
и
![]() ; б)
; б)
![]() и
и
![]() ;
;
в)
![]() и
и
![]() ; г)
; г)
![]() и
и
![]() .
.
