6.8. Формула Тейлора и ее приложения

Если функция дифференцируема раз в окрестности точки , то для любого имеет место формула Тейлора n-го порядка:

где – остаточный член в форме Лагранжа.

Приведем разложения некоторых функций по формуле Тейлора при , которые называются формулами Маклорена:

;

;

;

;

;

;

;

;

Остаточный член формулы Тейлора может быть представлен в форме Пеано: при .

П ример 6.23. Разложить многочлен по степеням двучлена

Решение. Поскольку – многочлен 4-й степени, то и формула Тейлора при имеет вид

.

Подставляя в эту формулу значения , получим

П ример 6.24. Написать формулу Тейлора 3-го порядка для функции в точке

Решение. Имеем:

По формуле Тейлора получаем

П ример 6.25. Вывести приближенную формулу и оценить ее точность при

Решение. Запишем формулу Тейлора 4-го порядка для функции в точке :

где

При имеем .

П оэтому с точностью .

П ример 6.26. Вычислить с точностью до .

Решение. Формула Тейлора для функции имеет вид

где

Полагая получим ,

где

Так как то

Определим наименьшее значение n так, чтобы выполнялось неравенство .

Е сли то , а если , то Поэтому с точностью до .

П ример 6.27. Вычислить

Используем формулу Тейлора с остаточными членами в форме Пеано:

.

Из последней формулы при получим

Искомый предел может быть переписан в виде

( поскольку при ).

7. Применение дифференциального исчисления для исследования функций и построения графиков

Одним изважнейших приложений производной является ее применение к исследованию функций и построению графиков функций.

7.1. Возрастание и убывание функции. Точки экстремума функции

Функция называется возрастающей (убывающей) в ин-тервале , если из неравенства , где , следует неравенство (или, соответственно, ).

Функция называется постоянной на интервале , если она принимает на этом интервале одно и то же значение.

Теорема 1 (достаточное условие возрастания (убывания) функ-ции). Если функция дифференцируема на интервале и для всех , то функция возрастает на , если же для всех , то убывает на этом интервале.

Возрастающие и убывающие функции называются монотонными. Определим условия постоянства функции.

Теорема 2 (необходимое и достаточное условия постоянства функции). Функция постоянна на интервале тогда и только тогда, когда в каждой точке интервала.

Функция имеет в точке минимум (локальный минимум) (максимум), если существует -окрестность точки ( ) такая, что для всякой точки из этой окрестности выполня-ется неравенство (или ). Точки минимума и максимума функции называются ее точками экстремума, а значения функции в этих точках называются экстремумами функции.

Сформулируем условия существования экстремума функции.

Теорема 3 (необходимое условие экстремума). Если – точка экстремума функции , то в этой точке или не существует.

Точка , в которой обращается в ноль или не существует, называется критической точкой функции .

Теорема 4 (первое достаточное условие экстремума). Пусть функция дифференцируема в некоторой окрестности ( ) критической точки , за исключением, быть может, самой точки и при переходе через нее (слева направо) производная меняет знак с плюса на минус, то есть точка максимума; если меняет знак с минуса на плюс, то – точка минимума функции . Если же сохраняет знак при переходе через точку , то не является точкой экстремума функции.

Теорема 5 (второе достаточное условие экстремума). Пусть функция дважды дифференцируема в критической точке и в некоторой ее окрестности ( ). Тогда, если , то – точка максимума функции , если , то – точка минимума . Если же , то требуются дополнительные исследования.

Отметим, что в точках экстремума дифференцируемой функции касательная к ее графику параллельна оси Ox.

На рис. 7.1 приведены примеры экстремумов функции.

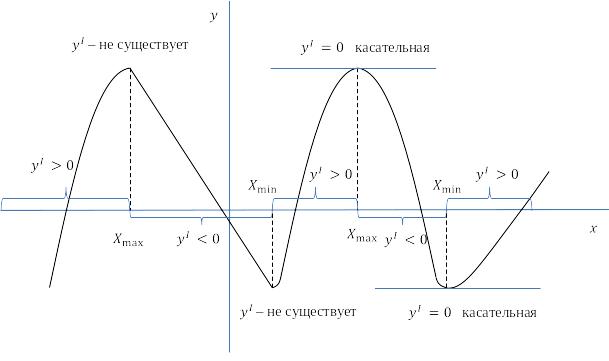
Рис. 7.1

Пример 7.1. Найти интервалы монотонности и точки экстремума функции .

Решение. Область определения этой функции: . Найдем производную: . Приравняв к нулю эту производную, получим . Следовательно, – критические точки функции (в точке не существует, но не входит в область определения функции). Эти точки разбивают область определения функции на интервалы монотонности. Исследуем знаки производной на этих интервалах, укажем вид интервалов монотонности функции, характер критических точек.

С ледовательно, – функция возрастает, – функция убывает, – точки максимума функции, – максимумы функции. Точек минимума нет.