7.9. Кривизна плоской линии

Одним из элементов, характеризующих форму кривой, является степень ее искривленности.

Рассмотрим кривую, которая не пересекает саму себя и имеет определенную касательную. Возьмем две точки A и B.

Углом смежности дуги AB называется угол поворота касательной при переходе от точки A к точке B (рис. 7.7).

Рис. 7.7

У двух дуг, имеющих одинаковую длину, больше изогнута та дуга, у которой угол смежности больше. Однако, степенью искривленности нельзя оценить форму дуги различной длины с одним и тем же углом смежности.

Средней кривизной дуги называется отношение соответ-ствующего угла смежности α к длине дуги:

.

Для одной и той же кривой средняя кривизна ее различных частей (дуг) может быть различна.

Кривизной линии в данной точке A называется предел средней кривизны дуги , когда длина этой дуги стремится к нулю (когда BA):

.

Предположим, что кривая задана в декартовой системе координат уравнением вида и пусть имеет непрерывную вторую производную.

Тогда кривизна плоской линии определяется по формуле

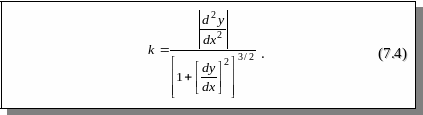
Заметим, что кривизна не может быть отрицательной.

Если кривая задана параметрически, то

.

Подставляя это в (7.4), получим кривизну плоской линии, заданной параметрически

П ример 7.10. Найти кривизну кривой в точке .

Решение. Найдем производные: ,

.

Т огда кривизна равна .

7.10. Понятие эволюты и эвольвенты

Величина R, обратная кривизне линии в данной точке M, называется радиусом кривизны этой линии в рассматриваемой точке, т. е.

.

Построим в точке M нормаль к кривой, направленной в сторону вогнутости кривой, и отложим на этой нормали отрезок MC, равный радиусу R (рис. 7.8) кривизны кривой l в точке M. Точка C называется центром кривизны данной кривой в точке M, круг радиуса R с центром в точке C (проходящий через точку M) называется кругом кривизны данной кривой в точке M.

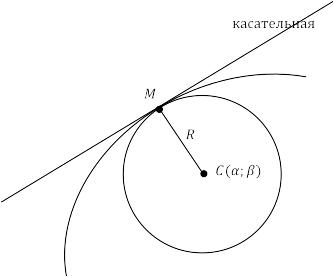
Рис. 7.8

Рассмотрим кривую . Если в точке данной линии кривизна отлична от нуля, то этой точке соответствует вполне определенный центр кривизны .

Совокупность всех центров кривизны данной линии образует некоторую новую линию, называемую эволютой по отношению к первой. Или: геометрическое место центров кривизны данной линии называется ее эволютой. По отношению к своей эволюте данная линия называется эвольвентой (инволютой или разверткой).

Теорема (свойство эволюты). Нормаль к данной кривой являет-ся касательной к ее эволюте.

7.11. Кривизна и кручение пространственной кривой. Формулы Френе

В любой точке пространственной кривой можно построить три взаимно перпендикулярных вектора:

Определим соответствующие им единичные векторы по фор-мулам:

Трехгранник с вершиной в точке M₀, ребрами которого служат касательная, главная нормаль, бинормаль, называется естественным трехгранником или трехгранником Френе. Гранями его являются плоскость соприкасающаяся (проходит через ), нормальная (проходит через ), спрямляющая (проходит через ) (рис. 7.9).

Рис. 7.9

Уравнения главной нормали имеют вид

где .

Уравнения бинормали:

где – координаты вектора , т.е. .

Заметим, что уравнения касательной могут быть записаны аналогично уравнению (7.2) в виде

где – координаты вектора .

Уравнение нормальной плоскости:

Уравнение соприкасающейся плоскости:

Уравнение спрямляющей плоскости:

Кривизна пространственной кривой определяется аналогично кривизне плоской кривой и в точке M вычисляется по формуле

Кручением пространственной кривой в точке M называется число , где  – угол поворота бинормали, соответствующий дуге . Если , то кручение  вычисляется по формуле

П ример 7.11. Найти единичные векторы , уравнения касательной, нормали, бинормали, уравнения соприкасающейся, нор-мальной и спрямляющей плоскостей, кривизну и кручение в точке винтовой линии (рис. 7.10).

Рис. 7.10

Решение. Находим

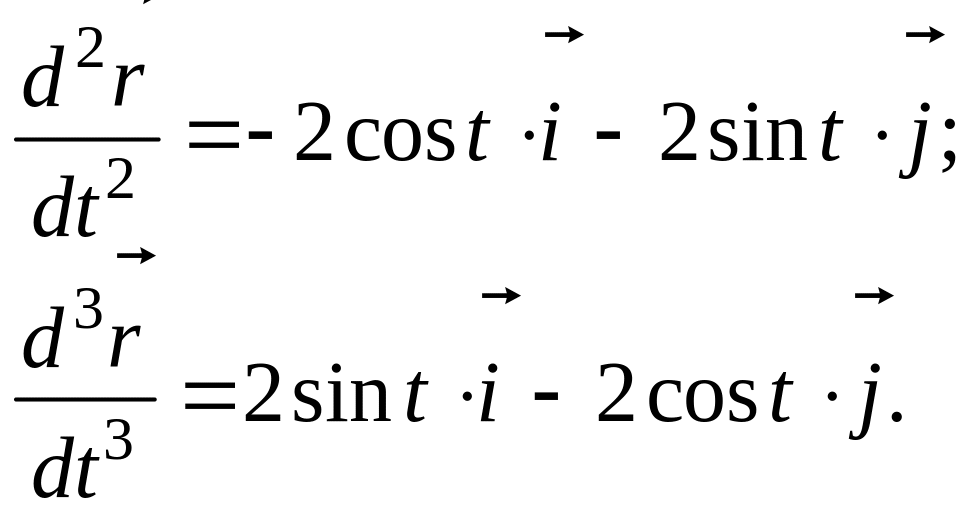
При ,

Находим единичные векторы :

Записываем уравнения граней трехгранника Френе:

– нормальная плоскость к винтовой линии в точке :

или ;

– соприкасающаяся плоскость к винтовой линии в точке :

или ;

– спрямляющая плоскость к винтовой линии в точке :

или .

Уравнения касательной в точке M:

;

уравнения нормали в точке M:

;

уравнения бинормали в точке M:

.

Находим кривизну винтовой линии в точке M:

.

Найдем в точке M: .

Кручение винтовой линии в точке M:

т . к. , то .

171