Расчет двухступенчатой передачи
Общее передаточное отношение планетарного
редуктора (рис.1в) разбивают по ступеням
и каждую ступень считают отдельно,
выполняя условия (2)…(5) или (6)…(9). Например,
для схемы рис.1,в можно принять передаточное
отношение ступеней одинаковым. Тогда
iaihi=ia2h2=
а дальнейший расчет можно продолжить
по методике расчета передачи 2К-h
с одновенцовым сателлитом.
Кпд планетарного редуктора и скорости вращения сателлитов
Для силовых передач одной из важнейших характеристик является цикловой КПД, то есть отношение работы сил полезного сопротивления к работе всех движущих сил за цикл установившегося движения.
КПД передачи 2К-h можно оценить по зависимости
,
(14)
а передачи 3 К – по зависимости
(15)
где
-коэффициент
потерь в зубчатых зацеплениях и
подшипниках сателлитов.
При сравнительной оценке КПД различных редукторов в курсовом проекте можно принять, что коэффициент потерь равен 0,05. Формулы (14) и (15) не учитывают потерь в подшипниках основной оси (входного ы выходного звеньев) и дают приемлемые результаты при оптимальных для данной схемы передаточных отношениях и моментах.
Для двухступенчатого редуктора (см.рис.1в) КПД определяется по правилу последовательно соединенных механизмов
а1h2=a1h1a2h2,
где a1h1 и a2h2 – КПД первой и второй ступени.
Другой важной характеристикой является скорость вращения сателлита относительно водила. Для схем (см. рис.1,а,б и 2) относительная угловая скорость вращения сателлита равна
g-h=-aZaZb/(Zg(Za+Zb)) (16)
или передаточное отношение от сателлита д к водилу h равно
(17)
Для схемы (см. рис.12,в) относительная скорость сателлита n1 определяется по формуле (22), а для сателлита д2 она равна
g2-h2=a1(-Zb2/Zg2)/
(18)
или передаточное отношение от сателлита д2 к водилу h2 равно
(19)
Вычерчивание схемы планетарной передачи
Схема планетарной передачи вычерчивается в двух проекциях в определенном масштабе (рис.3), причем допускается вычерчивать зубчатые колеса не по начальным, а по делительным окружностям d=mZ, где m- заданный модуль, Z – найденное число зубьев колес.
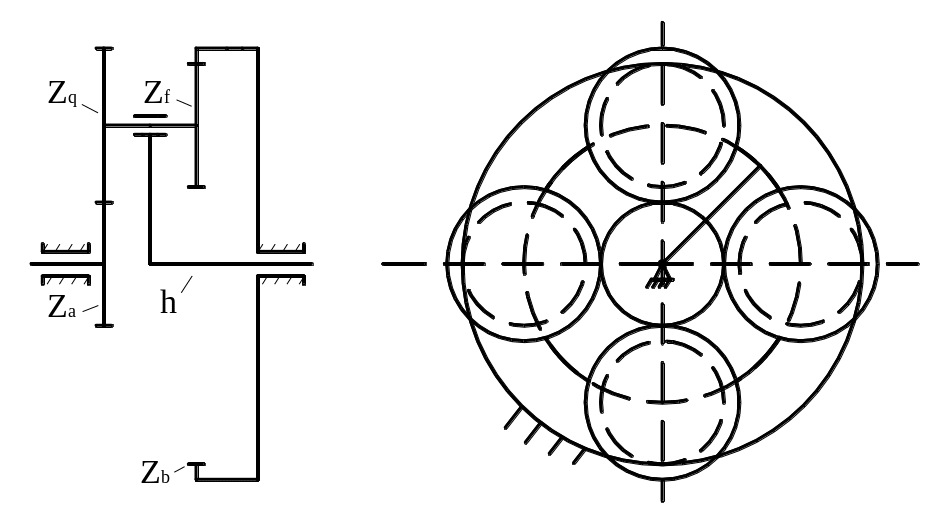
Рис.3. Схема планетарной передачи.