20. Графическое представление экспериментальных данных
Дли повышения наглядности эмпирических распределений, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма, полигон частот и полигон накопленных частот (кумулята).
2.3.1. Гистограмма
Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников, как показано на рис. 2.1. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте (или частости) попадания в данный интервал. Если ряд безинтервальный, то ширина всех столбцов выбирается произвольной, но одинаковые. Таким образом, высоты прямоугольников должны быть пропорциональны величинам
,
(2.6)
где ni — частота i-го интервала группировки; hi — ширина i-го интервала группировки.
На графике гистограммы основание прямоугольников откладывается по оси абсцисс (x), а высота — по оси ординат (у) прямоугольной системы координат.
Однако в тех случаях, когда ширина всех интервалов группировки одинакова, вид гистограммы не изменится, если по оси ординат откладывать не величины рi, а частоты интервалов ni.
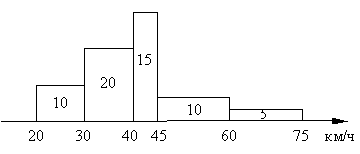
Рис. 2.1. Гистограмма распределения результатов в предыдущем примере (когда ширина некоторых интервалов группировки неодинакова).
В
этом случае чтобы не нарушить принцип
построения гистограммы (площади
прямоугольников пропорциональны
частотам интервалов), по оси ординат
уже нельзя откладывать частоты, а надо
– высоты прямоугольников (которые
должны быть пропорциональны отношениям 
).
2.3.2. Полигон частот
Другим распространенным способом графического представления является полигон частот.
Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у.
Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых. Пример полигона частот представлен на рис. 2.2.
Рис. 2.2. Полигон частот
Полигон частот используется для представления распределений как непрерывных, так и дискретных признаков. В случае непрерывного распределения полигон частот является более предпочтительным способом графического представления, чем гистограмма, если график эмпирического распределения описывается плавной зависимостью.
21. Гипо́теза (др.-греч. ὑπόθεσις — предположение; от ὑπό — снизу, под + θέσις — тезис) — предположение или догадка; утверждение, предполагающее доказательство, в отличие отаксиом, постулатов, не требующих доказательств. Гипотеза считается научной, если она удовлетворяет критерию Поппера, т.е. потенциально может быть проверена критическим экспериментом, а так же если она соответствует другим критериям, отличающим науку от не науки.
Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным. Примеры статистических гипотез в педагогических исследованиях:
Гипотеза 1. Успеваемость класса стохастически (вероятностно) зависит от уровня обучаемости учащихся.
Гипотеза 2. Усвоение начального курса математики не имеет существенных различий у учащихся , начавших обучение с 6 или 7 лет.
Гипотеза 3. Проблемное обучение в первом классе эффективнее по сравнению с традиционной методикой обучения в отношении общего развития учащихся.
Пример 1. Процесс производства некоторого медицинского препарата весьма сложен. Несущественные на первый взгляд отклонения от технологии вызывают появление высокотоксичной побочной примеси. Токсичность этой примеси может оказаться столь высокой, что даже такое ее количество, которое не может быть обнаружено при обычном химическом анализе, может оказаться опасным для человека, принимающего это лекарство. В результате, прежде чем выпускать в продажу вновь произведенную партию, ее подвергают исследованию на токсичность биологическими методами. Малые дозы лекарства вводятся некоторому количеству подопытных животных, например, мышей, и результат регистрируют. Если лекарство токсично, то все или почти все животные гибнут. В противном случае норма выживших велика.
Исследование лекарства может привести к одному из возможных способов действия: выпустить партию в продажу (а1), вернуть партию поставщику для доработки или, может быть, для уничтожения (а2).
Ошибки двух видов, связанные с действиями а1 и а2 совершенно различны, различна и важность избежания их. Сначала рассмотрим случай, когда применяется действие а1, в то время когда предпочтительнее а2. Лекарство опасно для пациента, в то время как оно признано безопасным. Ошибка этого вида может вызвать смерть пациентов, употребляющих этот препарат. Это ошибка первого рода, так как нам важнее ее избежать.
Рассмотрим случай когда предпринимается действие а2, в то время когда а1 является более предпочтительным. Это означает, что вследствие неточностей в проведении эксперимента партия нетоксичного лекарства классифицировалась как опасная. Последствия ошибки могут выражаться в финансовом убытке и в увеличении стоимости лекарства. Однако случайное отвержение совершенно безопасного лекарства, очевидно, менее нежелательно, чем, пусть даже изредка происходящие гибели пациентов. Отвержение нетоксичной партии лекарства – ошибка второго рода.
Допустимая вероятность ошибки первого рода (Ркр) может быть равна 5% или 1% (0.05 или 0.01).
22. Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.