17. Что выступает в качестве точечных оценок параметров?

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки, полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр. Рассматривая значения количественного признака как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения - это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

Поясним каждое из понятий.

  Несмещенной называют статистическую оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.

M(Q^*) = Q.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

  Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

  Состоятельной называют статистическую оценку, которая при п®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п®¥ стремится к нулю, то такая оценка оказывается и состоятельной.

Рассмотрим точечные оценки параметров распределения, т.е.

оценки, которые определяются одним числом Q^* =f( x₁, x₂,…,x_n), где x₁, x₂,…,x_n- выборка.

18. Выборочные числовые характеристики, формулы для их подсчета.

Для выборки СВ и для статистического ряда определяются следующие числовые характеристики.

О: Средним арифметическим выборки называется средним арифметическим статистического ряда (36.1): Дисперсией выборки называется дисперсией статистического ряда (36.1) — Средним квадратическим отклонением называется

Пусть — случайная величина с функцией распределения где — неизвестный параметр распределения, т.е. неизвестная числовая характеристика СВ Например, имеет нормальное распределение с неизвестным параметром Рассмотрим выборок этой СВ Обозначим через оценку величины 9, ее можно представить как случайную величину, зависящую от Чтобы выбрать в некотором смысле лучшую оценку рассматриваются свойства оценок: несмещенность, состоятельность, эффективность.

О: Оценка параметра называется несмещенной, если ее математическое ожидание состоятельной,

если по вероятности сходится к при

т.е. Несмещенная оценканазывается эффективной, если ее дисперсия — наименьшая среди всех дисперсий, вычисляемых для оценок по выборкам одинакового объема.

Т: Среднее арифметическое М* выборки случайной величины имеющей математическое ожидание и дисперсию является несмещенной и состоятельной оценкой математического ожидания. В случае нормального распределения СВ эта оценка является эффективной. Доказательство в [7. С. 505].

В качестве оценки математического ожидания генеральной совокупности берется среднее арифметическое М* выборки. Выборочная дисперсия D* является смещенной состоятельной оценкой дисперсии, поэтому в качестве несмещенной состоятельной оценки дисперсии генеральной совокупности используется исправленная выборочная дисперсия

( — объем выборки), S— исправленное среднее квадратическое отклонение. Если объем выборки достаточно большой то и в качестве оценки генеральной дисперсии берется D*.

Пример 3: Найти параметры распределения случайной величины в примере 2 разд. 36.1, если имеет нормальный закон распределения.

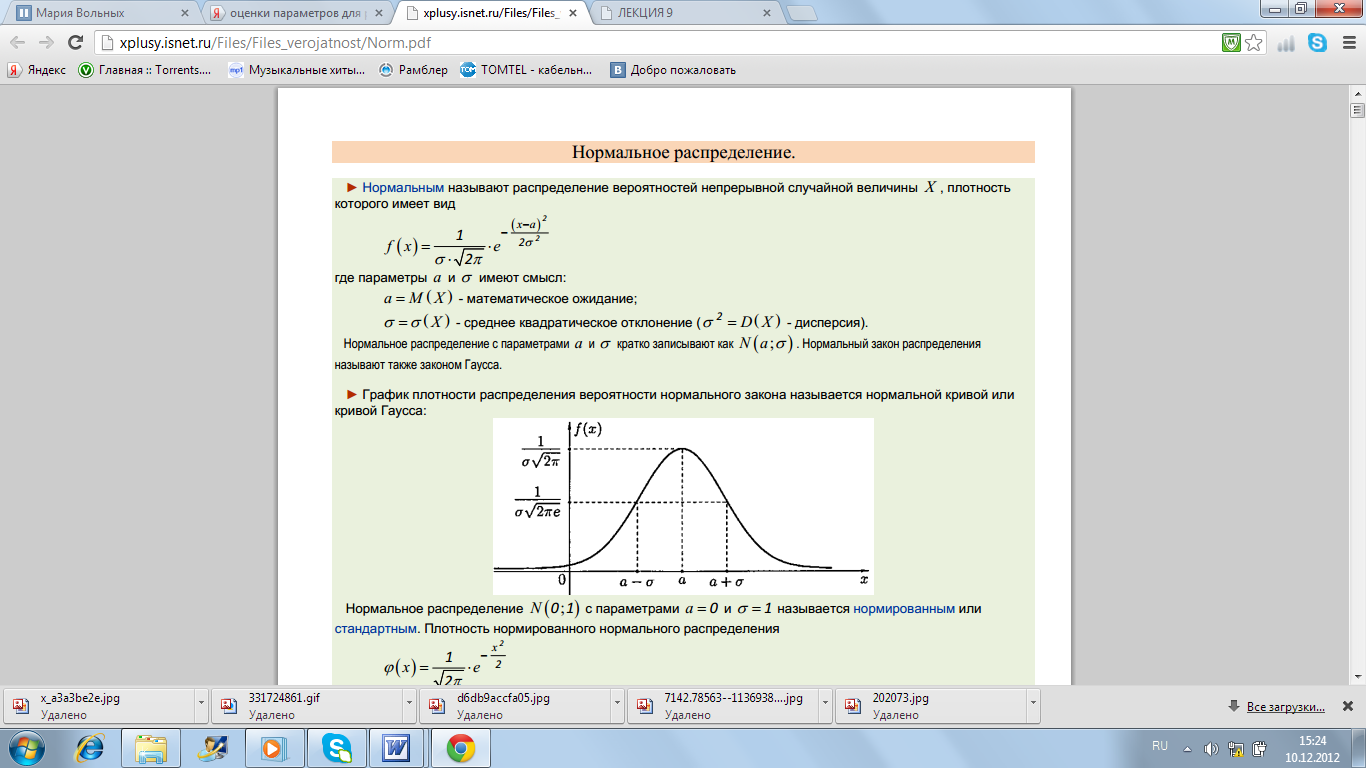
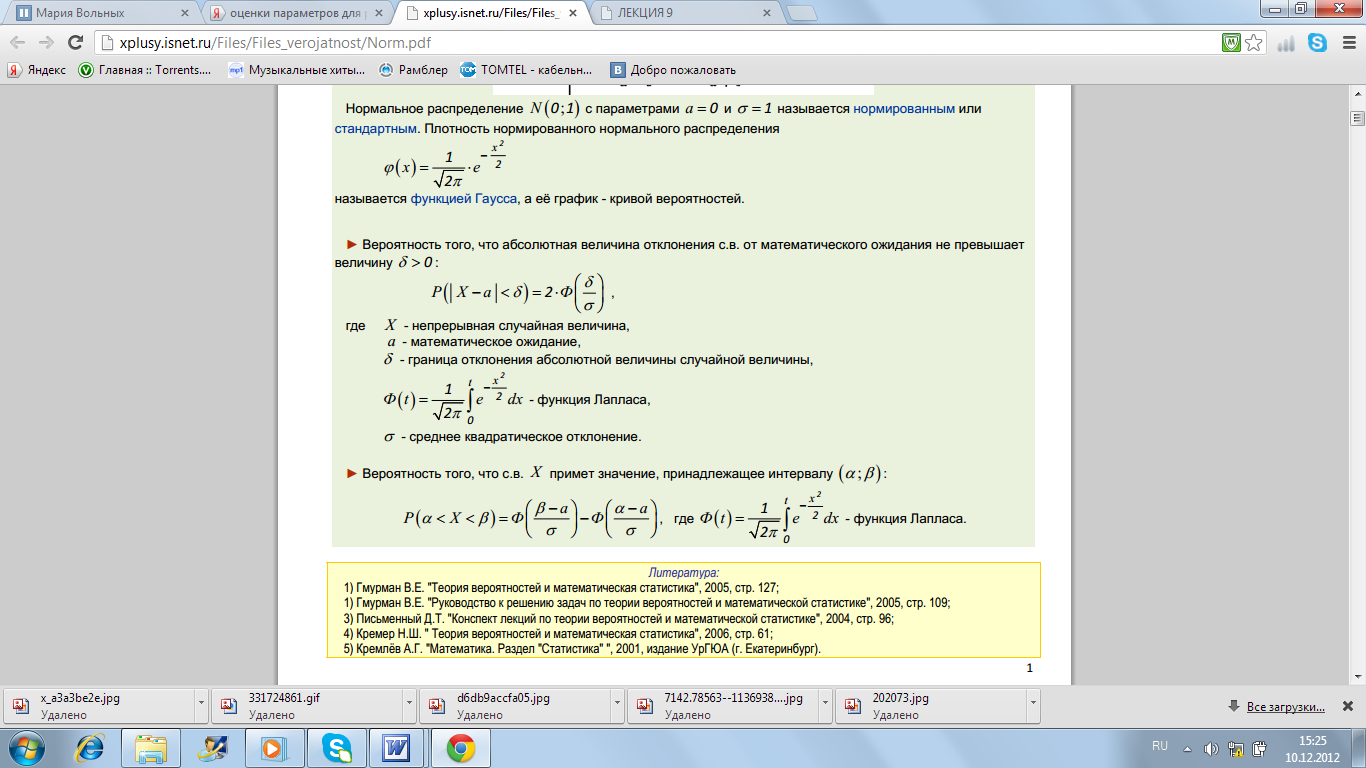
Плотность вероятности для нормального закона распределения

неизвестные параметры —

Так как

 Равномерное рапределение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероят­ности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

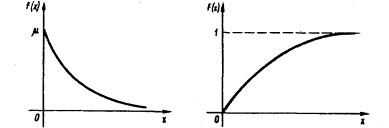
ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ Непрерывная случайная величина X, функция плотности которой задается выражением

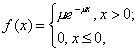
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение.

Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.