11. Понятие статистического закона распределения.

Предположим, что изучается дискретная или непрерывная случайная величина, закон распределения которой неизвестен. Для оценки закона распределения этой случайной величины и его числовых характеристик производится ряд независимых измерений x₁, x₂, ..., x_n.Статистический материал представляют в виде таблицы, состоящей из двух строк, в первой из которых даны номера измерений, а во второй — результаты измерений.

i — номер измерения	1	2	....
xi — результат измерений	x1	х2	....	хn

Такую таблицу называют простым статистическим рядом.

Для того чтобы правильно оценить закон распределения СВ Х, производят группировку данных. Если X — дискретная СВ, то наблюденные значения располагаются в порядке возрастания и подсчитываются частоты m_i или частости m_i/n появления одинаковых значений СВ Х. В результате получаем сгруппированные статистические ряды:

хi	x1	х2	....	хk
mi	m1	m2	....	mk

Контроль: åm_i = n .

хi		х1	х2	......	хn
mi/n		m1/n	m2/n	......	mk/n

Контроль: åm_i/n = 1.

Если изучается непрерывная случайная величина, то группировка заключается в разбиении интервала наблюденных значений случайной величины на k частичных интервалов равной длины [x₀; x₁ [, [x₁; x₂ [, [x₂; x₃ [, ...... [x_k-1;x_k] и подсчете частоты или частости m_i/n попадания наблюденных значений в частичные интервалы. Количество интервалов выбирается произвольно, обычно не меньше 5 и не больше 15.

В результате составляется интервальный статистический ряд следующего вида:

СВХ	[x0; x1 [	[x1; x2 [	....	[xk-1;xk]
mi/n	m1/n	m2/n	....	mk/n

Контроль: å m_i/n = 1.

Определение. Перечень наблюденных значений СВ Х (или интервалов наблюденных значений) и соответствующих им частостей m_i/n называется статистическим законом распределения случайной величины.

Статистические законы позволяют визуально произвести оценку закона распределения исследуемой случайной величины.

12. Графическое представление выборки (полигон, гистограмма). Их разновидности.

Наиболее часто используют следующие виды графического пред­ставления характеристик выборки: полигон, гистограмма и кумуля­тивная кривая. Гистограмма и полигон позволяют выявить преобладающие значения признака и характер распределения частот и относительных частот. Полигон служит обычно для представления дискретного вариационного ряда. В системе координат (x, m_х,) или (х, ) строятся точки, соответствующие значениям частот или относительных частот ряда, а затем эти точки соединяются прямыми линиями. На рис. 2.2.1 показан полигон частот для ряда, представленного табл. 2.1.1. Гистограмма — это диаграмма, используемая, как правило, для представления интервального вариационного ряда. Наиболее суще­ственное отличие от полигона в том, что частота и относительная частота отображаются не точкой, а прямой, параллельной оси абсцисс на всем интервале. Это объясняется тем, что данная частота (относительная частота) от­носится не к дискретному значению признака, а ко всему интервалу (рис. 2.2.2). Иногда и интервальный ряд изображают в виде полигона. В этом случае значение частоты или относительной частоты для каждого интервала относят к середине интервала. Кумулятивная кривая строится для накопленных частот или накопленных относительных частот, причем по оси ординат откладывают верхнюю границу интервала соответствующего интервального ряда, так что последняя точка кумулятивной кривой всегда отвечает либо количеству наблюдений в выборке, либо единице (рис. 2.2.3). Рис. 2.2.3. Кумулятивная кривая накопленных частот

13. Как можно выдвинуть предположение (гипотезу) о виде распределения по наблюдениям за случайной величиной.величины на основе опытных данных" width="17" height="20" align="BOTTOM" border="0" />, оба параметра неизвестны.Пусть х1, х2, х3, …, хn – выборка, полученная в результате проведения n независимых наблюдений случайной величины Х. Чтобы подчеркнуть случайный характер величин х1, х2, х3, …, хn перепишем их в виде:Х1, Х2, Х3, …, Хn, где Хi – значение случайной величины Х в i-ом опыте.Требуется на основании этих опытных данных оценить математическое ожидание и дисперсию случайной величины. Такие оценки называются точечными, в качестве оценки m и D можно принять статистическое математическое ожидание и статистическую дисперсию , где

До проведения опыта выборка Х1, Х2, Х3, …, Хn есть совокупность независимых случайных величин, которые имеют математическое ожидание и дисперсию, а значит распределение вероятности такие же как и сама случайная величина Х. Таким образом:

, , где i = 1, 2, 3, …, n.

Исходя из этого, найдем математическое ожидание и дисперсию случайной величины (пользуясь свойствами математического ожидания).

Таким образом математическое ожидание статистического среднего равно точному значению математического ожидания m измеряемой величины, а дисперсия статистического среднего в n раз меньше дисперсии отдельных результатов измерений.

при Это значит, что при большом объеме выборки N статистическое средние является величиной почти неслучайной, оно лишь незначительно отклоняется от точного значения случайной величины m. Этот закон называется законом больших чисел Чебышева.

Точность статистической оценки. Доверительная вероятность (надежность оценки), доверительный интервал

Точечные оценки неизвестных значений математического ожидания и дисперсии имеют большое значение на первоначальном этапе обработки статических данных. Их недостаток в том, что неизвестно с кокой точностью они дают оцениваемый параметр.

Пусть по данной выборке Х1, Х2, Х3, …, Хn получены точные статистические оценки и , тогда числовые характеристики случайной величины Х будут приближенно равны . Для выборки небольшого объема вопрос поточности оценки существенен, т.к между m и , D и будут недостаточно большие отклонения. Кроме того при решении практических задач требуется не только найти приближенные значения m и D, но и оценить их точность и надежность. Пусть ,т.е является точечной оценкой для m. Очевидно, что тем точнее определяет m, чем меньше модуль разности . Пусть , где ε>0, тогда, чем меньше ε, тем точнее оценка m. Таким образом, ε>0 характеризует точность оценки параметра. Однако статистические методы не позволяют категорически утверждать, что оценка истинного значения m удовлетворяет , можно лишь говорить о вероятности α, с которой это неравенство выполняется:

Таким образом, α- это доверительная вероятность или надежность оценки, значение α выбираются заранее в зависимости от решаемой задачи. Надежность α принято выбирать 0.9; 0.95; 0.99; 0.999. События с такой вероятностью являются практически достоверными. По заданной доверительной вероятности можно найти число ε>0 из .

Тогда получим интервал ,который накрывает с вероятностью α истинное значение математического ожидания m, длина этого интервала равна 2ε. Этот интервал называется доверительным интервалом. А такой способ оценки неизвестного параметра m – интервальным.

Доверительный интервал для математического ожидания нормального распределения случайной величины при известном σ.

Пусть дана выборка Х1, Х2, Х3, …, Хn, и пусть по этой выборке найдено , , .

Требуется найти доверительный интервал для математического ожидания m с доверительной вероятностью α. Величина есть величина случайная с математическим ожиданием , .

Случайная величина имеет суммарную природу, при большом объеме выборки она распределена по закону близкому к нормальному. Тогда вероятность попадания случайной величины в интервал будет равна:

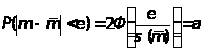
,где 4

Где- функция Лапласа.

Из формулы (3) и таблиц функции Лапласа находим число ε>0 и записываем доверительный интервал для точного значения случайной величины Х с надежностью α.

В этой курсовой работе значение σ заменим , и тогда формула (3) примет вид:

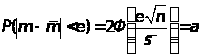
Найдем доверительный интервал , в котором находится математическое ожидание. При α = 0.99, n = 100, , .

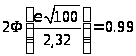
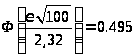
по таблицам Лапласа находим:

Отсюда ε = 0,5986.

- доверительный интервал, в котором с вероятностью 99% находится точное значение математического ожидания.