6. Множественная линейная регрессия

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных X₁, X₂, …, X_k. Эта задача решается с помощью множественного регрессионного анализа.

Модель множественной линейной регрессии имеет вид

; (2.42)

или

_{; .}

_{(i=1,…,n) (2.43)}

Модель (2.42), в которой зависимая переменная , возмущения и объясняющие переменные ,…, удовлетворяют приведенным выше предпосылкам 1–5 регрессионного анализа, называется классической нормальной линейной моделью множественной регрессии.

Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений.

Введем обозначения:

– вектор-столбец значений зависимой переменной размера n;

Х=

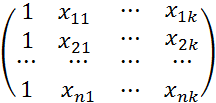
– матрица значений объясняющих переменных размера n(k+1).

где x_ij – значение j-й переменной для i-го объекта выборки.

Обращаем внимание на то, что в матрицу Х дополнительно введен столбец, все элементы которого равны 1, т. е. условно полагается, что в модели (2.42) свободный член умножается на фиктивную переменную , принимающую значение 1 для всех i: ;

– вектор-столбец параметров размером k+1;

– вектор-столбец возмущений (случайных ошибок, остатков) размера n.

Тогда в матричном виде модель (2.42) примет вид

(2.44)

Как уже было отмечено, модель (2.44), удовлетворяющая приведенным предпосылкам 1–5, называется классической нормальной линейной моделью множественной регрессии. Если же среди приведенных предпосылок не выполняется лишь предпосылка 5 о нормальном законе распределения вектора возмущений ε, то модель (2.44) называется просто классической линейной моделью множественной регрессии.

Оценки параметров а₀, a₁, … a_k можно получить с помощью рассмотренного ранее метода наименьших квадратов.

Система уравнений имеет вид

,

,

……..

.

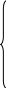Суммирование производится по индексу i от 1 до n, где n – объем выборки.

Эту систему обычно записывают в матричном виде

,

где – транспонированная матрица.

Умножив обе части уравнения слева на матрицу , получим

_. (2.45)

Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у₁, у₂, … у_n.

При выполнении предпосылок множественного регрессионного анализа оценка метода наименьших квадратов является эффективной, т. е. обладает наименьшей дисперсией в классе линейных несмещенных оценок.

Преобразуем вектор оценок (2.45) с учетом (2.44):

_или

= , (2.46)

т. е. оценки параметров (2.45), найденные по выборке, будут содержать случайные ошибки.

Покажем, что математическое ожидание оценки равно оцениваемому параметру :

,

так как . Таким образом, очевидно, что вектор есть несмещенная оценка вектора параметров .

Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу оценок параметров :

= ,

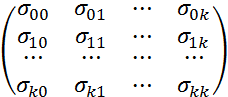где – ковариации оценок параметров и . Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий. Поэтому

_. (2.47)

Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.

В силу того, что оценки , полученные методом наименьших квадратов, являются несмещенными оценками параметров , т. е. , выражение (2.47) примет вид

.

Рассматривая ковариационную матрицу , легко заметить, что на ее главной диагонали находятся дисперсии оценок параметров регрессии, так как

. (2.48)

В матричном виде ковариационная матрица вектора оценок параметров имеет вид

(в этом легко убедиться, перемножив векторы и ).

Учитывая (2.46), преобразуем это выражение:

(2.49)

ибо элементы матрицы Х – неслучайные величины.

М атрица представляет собой ковариационную матрицу вектора возмущений:

,

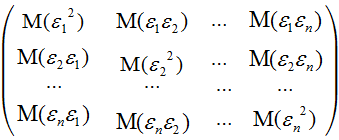в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки о некоррелированности возмущений и между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок регрессионного анализа равны одной и той же дисперсии :

.

Поэтому матрица

,

где – единичная матрица n-го порядка. Следовательно, в силу (2.49) ковариационная матрица вектора оценок параметров:

или _. (2.50)

Итак, с помощью обратной матрицы определяется не только сам вектор оценок параметров, но и дисперсии и ковариации его компонент.

Прогноз по модели множественной линейной регрессии для вектора переменных составит

. (2.51)

Дисперсия ошибки прогноза определяется по формуле

. (2.52)

В качестве оценки используется

. (2.53)

Тогда оценка дисперсии ошибки прогноза

_{. (2.54)}

Качество всей модели в целом определяется по критерию Фишера

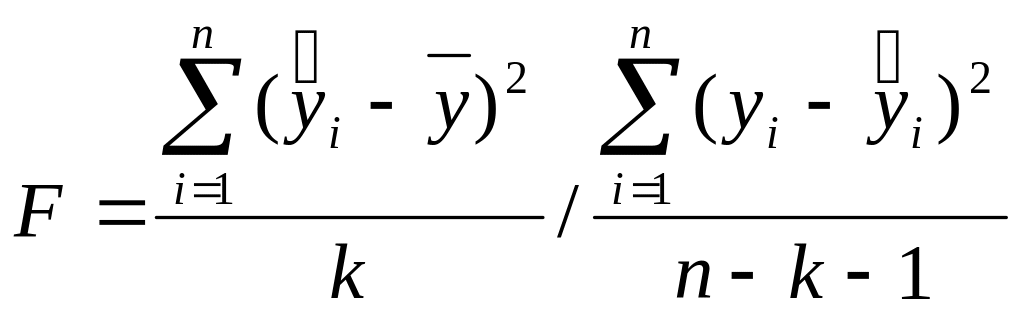. (2.55)

Если , то уравнение регрессии в целом незначимо. Здесь – табличное значение критерия Фишера с k и n-k-1 степенями свободы уровня значимости .

Может быть рассчитан коэффициент детерминации, отражающий долю объясненной факторами дисперсии в общей дисперсии:

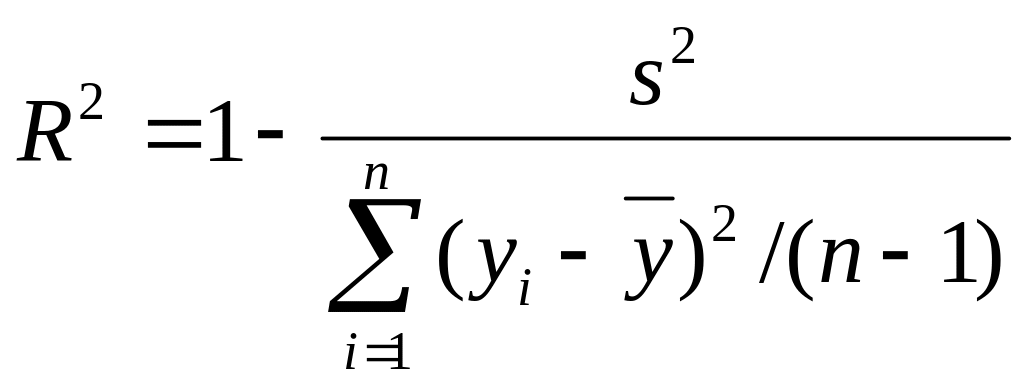. (2.56)

Правило проверки статистической значимости оценок (i=0,…,k) основывается на проверке статистической гипотезы

Н₀: .

Для этого вычисляется статистика

, (2.57)

которая при выполнении гипотезы Н₀ распределена по закону Стьюдента с n-k-1 степенями свободы.

Если , гипотезу Н₀ следует отклонить и признать коэффициент статистически значимым. В противном случае следует признать статистически незначимым и переменную X_i исключить из регрессионной модели.