4.11. Основные проблемы идентификации статистических моделей прогнозирования

Следует отметить, что для различных временных рядов их математическая аппроксимация может иметь разное аналитическое выражение. Поэтому на практике необходимо иметь широкий набор математических зависимостей, включая зависимости (1.2) – (1.5) и т. д.

Для выбора той или иной модели из рассматриваемого класса необходим некоторый критерий. В задачах регрессионного анализа в качестве такого критерия традиционно используется нормированная к числу степеней свободы сумма квадратов отклонений истинных значений рассматриваемой величины от расчетных (критерий минимума остаточной дисперсии).

Однако, как показывает практика, такой подход в прогнозировании приводит к моделям, обладающим плохими прогнозирующими свойствами. В связи с этим в ряде работ производится разделение выборки на обучающую (используемую для оценки параметров моделей) и контрольную (используемую для оценки точности прогноза) части. При этом в качестве критерия выбора модели используется минимум средней квадратичной ошибки в контрольной выборке. Такой подход является более перспективным, однако к его недостаткам следует отнести потери части информации как при идентификации модели, так и при оценке ее параметров. Поэтому аналитическая оценка дисперсии ошибки прогноза, обусловленной ошибками оценки параметров моделей и случайной составляющей, и ее использование в качестве критерия выбора модели представляется предпочтительней.

Следует отметить, что априорная аналитическая оценка дисперсии ошибки прогноза является весьма условной, так как мы не застрахованы от других видов ошибок.

Вообще говоря, к возможным причинам ошибочности прогнозов можно отнести:

– методические ошибки (неудачный выбор метода прогнозирования для данного объекта, неправильный выбор (неадекватность) математической модели прогнозирования, ошибки оценок параметров модели, неправомерность распространения существовавших в прошлом тенденций и функциональных связей на будущее);

– недостаток информации (недостоверность и неполнота используемой для прогноза статистической информации, квантование времени при построении временных рядов);

– случайность (воздействие случайных факторов, приводящее к случайной составляющей модели, редкие непредсказуемые события).

Наибольший вопрос при применении экстраполяционного метода прогнозирования всегда вызывает правомерность распространения прошлых тенденций на будущее. Со временем могут изменяться как параметры моделей, так и сами математические зависимости, происходить различные качественные изменения (скачки).

Процессы, для которых характерно плавное изменение математической зависимости, должны описываться с помощью адаптивных моделей.

И, наконец, учесть редкие непредсказуемые события практически невозможно. Поэтому можно согласиться с авторами работы, которые считают прогноз эффективным, если он снижает уровень неопределенности по сравнению с природным (по многолетнему среднему) или инерционным (завтра как сегодня) прогнозом.

Задание 3

Выберите из таблицы временной ряд в соответствии с номером Вашего варианта (по последней цифре шифра зачетной книжки)

Номер варианта	Временной ряд
	1	2	3	4	5
1	26,7	28,1	30,3	32,1	34,0
2	616	635	657	707	716
3	85,4	87,2	93,4	97,1	97,2
4	865	867	910	999	1025
5	304	325	344	359	386
6	212,3	216,2	219,8	223,2	226,4
7	145,0	152,9	164,6	168,8	181,3
8	59,1	56,1	58,9	58,4	57,5
9	78,5	81,1	87,3	91,7	96,4
10	292,3	327,6	369,3	412,4	458,9

1. Рассчитать показатели динамики – абсолютный прирост, коэффициент роста, коэффициент прироста (цепные и базисные).

2. Найти средний абсолютный прирост и средний коэффициент роста.

3. Подобрать линейную зависимость вида 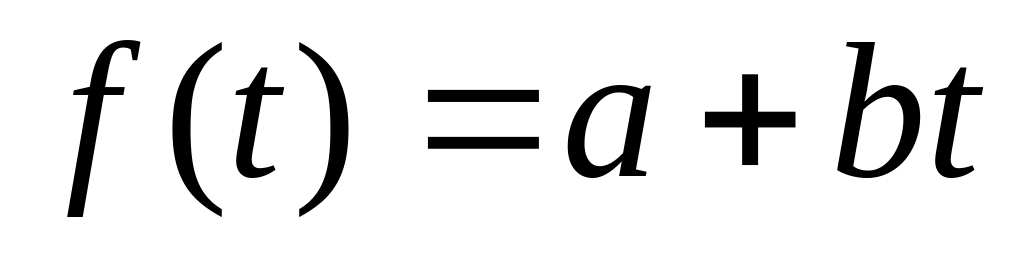. Найти оценки коэффициентов и 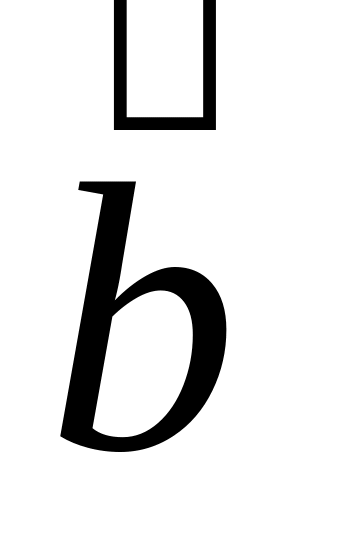по методу наименьших квадратов.

4. Сделать прогноз показателя по математической модели тренда на 3 года вперед.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Айвазян, С. А. Эконометрика: учеб. пособие для студентов вузов/ С.А. Айвазян – М. : Маркет ДС, 2007.– 98 с.

2. Айвазян, С. А. Прикладная статистика и основы эконометрики/С. А. Айвазян, В. С. Мхитарян. – М.: ЮНИТИ, 1998.

3. Афанасьев, В. Н. Эконометрика: учеб. для студентов вузов/ В. Н. Афанасьев. – М. : Финансы и статистика, 2006. – 255 с.

4. Афанасьев, В. Н. Анализ временных рядов и прогнозирование: учеб./В. Н. Афанасьев, М. М. Юзбашев. – М.: Финансы и статистика, 2001. – 228 с.

5. Богданов, А. И. Математические модели прогнозирования: монография/А. И. Богданов.- СПб.: СПГУТД, 2007. – 128 с.

6. Буре, В. М. Основы эконометрики: учеб. пособие/ В. М. Буре, Е. А. Евсеев. – СПб.: СПбГУ, 2004. – 40 с.

7. Дубина, И. Н. Математико-статистические методы в эмпирических социально-экономических исследованиях: учеб. пособие по дисциплине «Эконометрика»/И. Н. Дубинина. – М.: Финансы и статистика, 2010. – 413 с.

8. Елисеева, И. И. Практикум по эконометрике: учеб. пособие/И. И. Елисеева. – М.: Финансы и статистика, 2005. – 189 с.

9. Елисеева, И. И. Общая теория статистики. – 5-е изд/ И. И. Елисеева, М. М. Юзбашев. – М.: Финансы и статистика, 2006.

10. Колемаев, В. А. Эконометрика: учеб. для студентов вузов по специальности «Математические методы в экономике»/ В. А. Колемаев. – М. : ИНФРА-М, 2007. – 160 с.

11. Кремер, Н. Ш. Эконометрика / Н. Ш. Кремер, Б. А. Путко. под ред. Н. Ш. Кремера, – 3-е изд. – М.: ЮНИТИ, 2010. – 328 с.

12. Маленво, Э. Статистические методы в эконометрии/Э. Маленво. – М. : Статистика, 1976.

13. Орлов, А. И. Эконометрика: учеб. для вузов. – 4-е изд/А. И. Орлов. – Ростов н/Д: Феникс, 2009. – 572 с.

14. Фишер, Ф. Проблемы идентификации в эконометрии/Ф. Фишер. – М.: Статистика, 1978.

15. Эконометрика / под ред. И. И. Елисеевой. –2-е изд. – М.: Финансы и статистика, 2005. – 576 с.

16. Юзбашев, М. М. Эконометрика : учеб. пособие/ М. М. Юзбашев.– М.: Финансы и статистика, 2003.

84