10. Диагностическая проверка адекватности моделей. Критерий Дарбина–Уотсона

Формально качество модели определяется ее адекватностью и точностью прогноза.

Модель считается адекватной, если ряд остатков удовлетворяет требованиям нулевого среднего, случайности, независимости последовательных значений и в ряде случаев нормальности.

Для проверки свойства нулевого среднего рассчитывается среднее значение остатков:

.

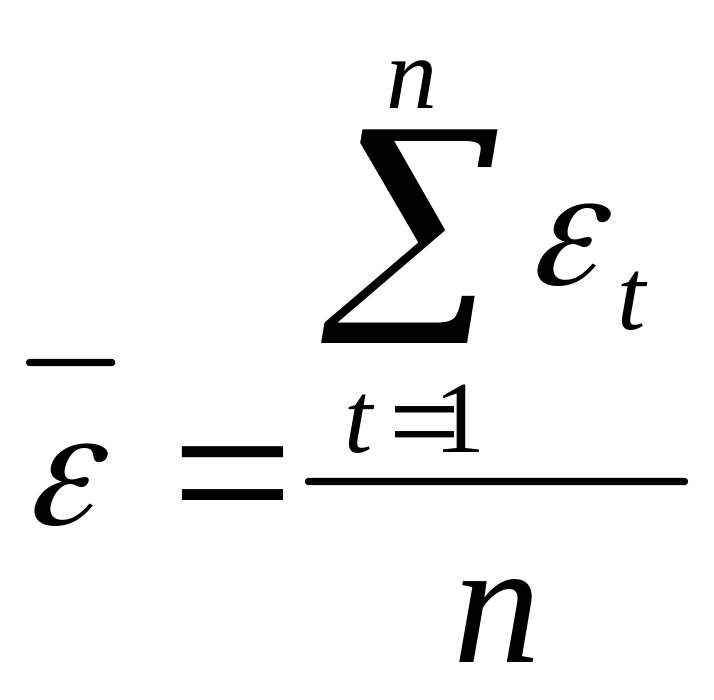Если близко к нулю, то можно считать, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего. Этот вопрос может быть решен со статистических позиций.

.

Гипотеза принимается, если

,

где 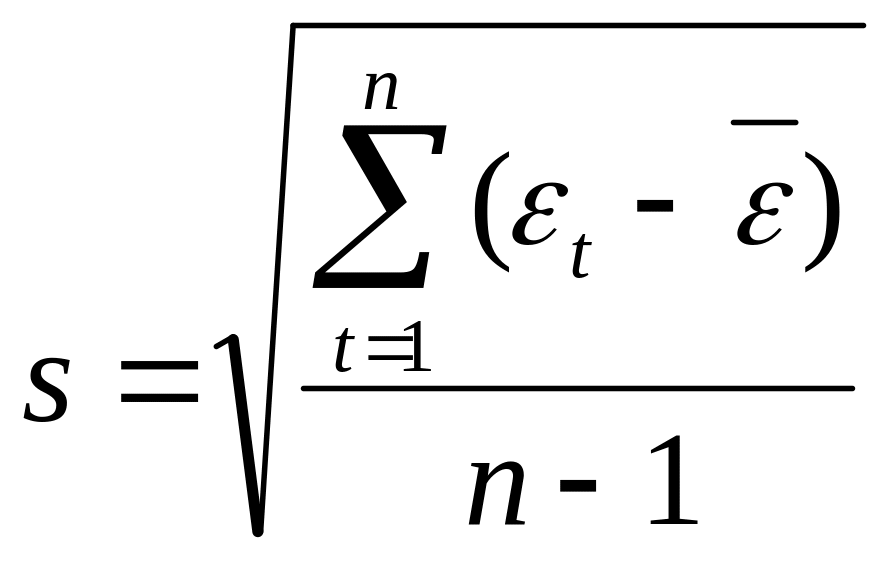– среднее квадратичное отклонение остатков;

– табличное значение критерия Стьюдента с n-1 степенью свободы уровня значимости .

Далее осуществляется проверка остаточного ряда по критерию случайности.

Проверка независимости последовательных остатков может осуществляться также по критерию Дарбина–Уотсона:

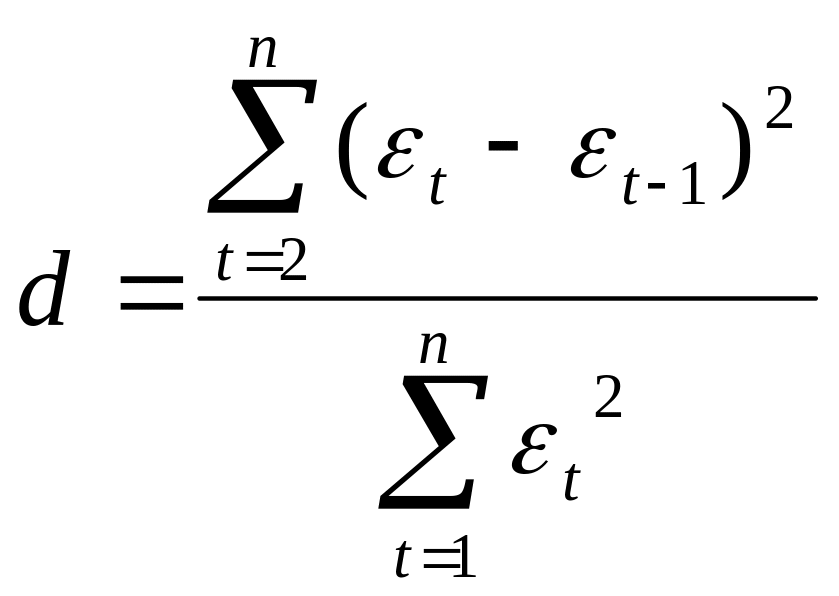. (4.51)

Несложные вычисления позволяют проверить, что статистика Дарбина–Уотсона следующим образом связана с выборочным коэффициентом корреляции между соседними наблюдениями.

(4.52)

В самом деле

.

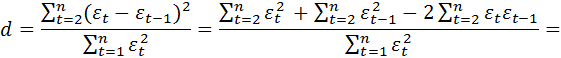
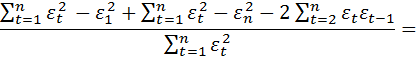
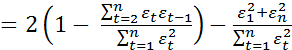При большом числе наблюдений n сумма значительно меньше и

,

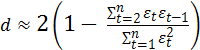откуда и следует приближенное равенство (4.52), так как в силу условия

.

Естественно, что в случае отсутствия автокорреляции выборочный коэффициент окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум.

Для рядов с тесной взаимосвязью между последовательными уровнями значение d близко к нулю; это свидетельствует о том, что регулярная составляющая не полностью отражена в модели тренда, т. е. модель не адекватна реальному процессу. Если последовательные остатки независимы, то d близко к 2, и это свидетельствует о хорошем качестве модели. При отрицательной автокорреляции остатков (строго периодическом чередовании их знаков) d близко к 4.

Заметим, что тест Дарбина–Уотсона, вообще говоря, не представляет собой статистический критерий в том смысле, что нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось что в эту область попало наблюдаемое значение статистики d.

Тест работает следующим образом.

Если d , то значение d сравнивается с табличными значениями d_L и d_U:

– если , то гипотеза о независимости отвергается;

– если , то гипотеза о независимости принимается;

– если , то нет достаточных оснований для принятия решения.

Если , то с критическими значениями d_L и d_U, взятыми из таблиц, сравнивается не d, а 4- d и решение принимается по тем же правилам.

Изобразим результат Дарбина –Уотсона в виде таблицы.

0<
Н0 отвергается (положительная автокорреляция)	Зона неопреде-ленности	Н0 принимается (отсутствие автокорреляции)	Зона неопреде-ленности	Н0 отвергается (отрицательная автокорреляция)

Совокупный критерий согласия Бокса–Пирса рассматривает совокупность первых k автокорреляций ряда остатков  ₁(), ₂(),…, _k():

.

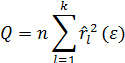Статистика Q имеет ²– распределение с k-m-1 степенями свободы. Пороговое значение для величины Q определяется по таблице.

Нормальность ряда остатков проверяется с целью использовать это свойство в дальнейшем при построении доверительных интервалов прогноза.

Ввиду малого числа наблюдений в большинстве временных рядов (меньше 30) это свойство может быть проверено лишь посредством вычисления оценок коэффициентов асимметрии и эксцесса для ряда остатков

; ,

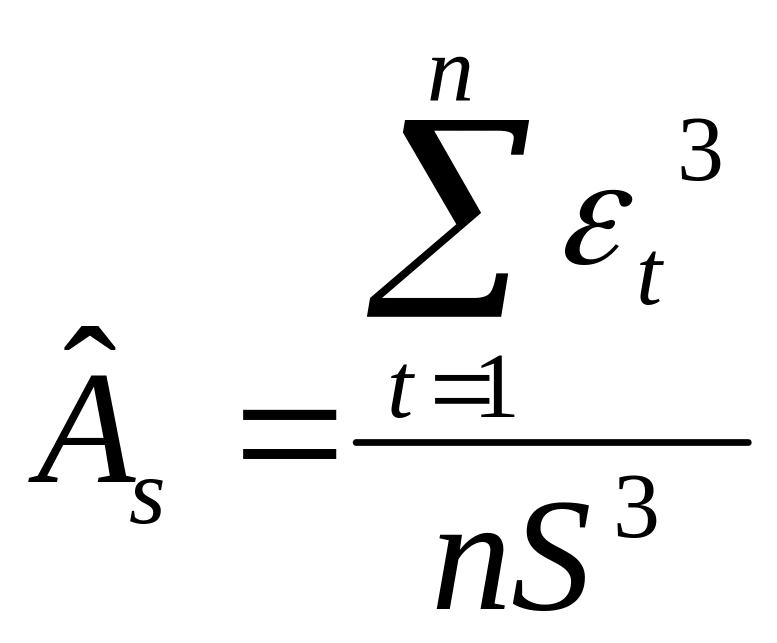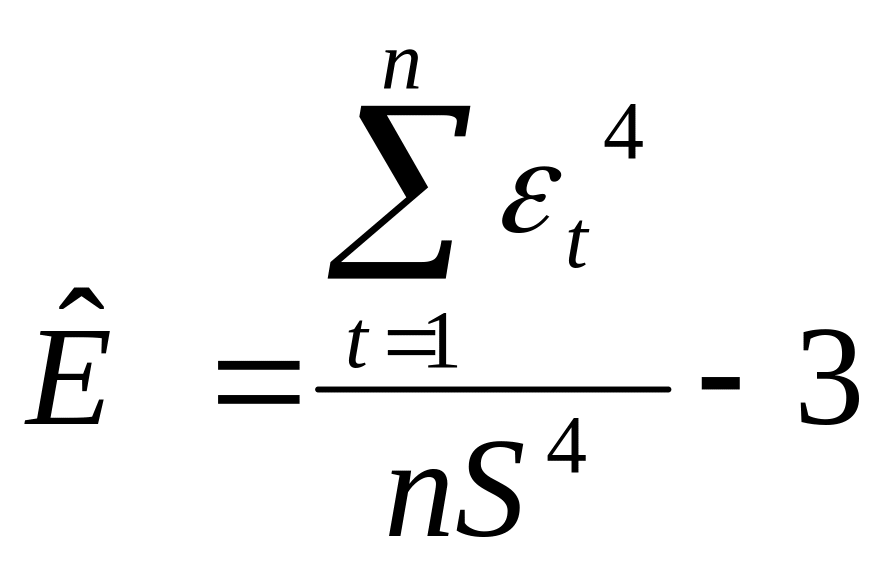где S – средняя квадратичная ошибка

.

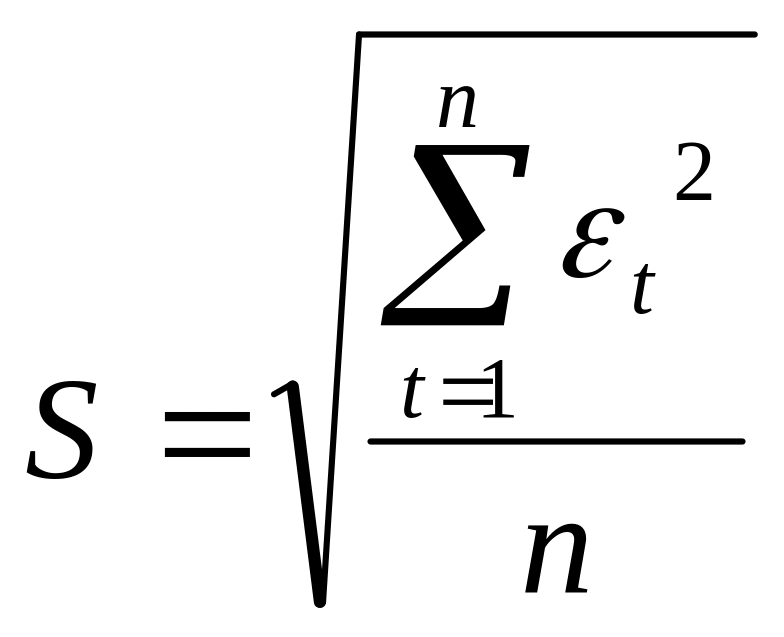Для нормального распределения и .

Гипотеза Н₀ о нормальном распределении ряда остатков ( ; ) принимается, если выполняются соотношения:

;

.

В этом случае доверительные интервалы для прогноза будут достаточно достоверными.