2. Системы одновременных уравнений

1. Системы независимых и взаимосвязанных (совместных) уравнений

Сложные экономические процессы описываются с помощью системы взаимосвязанных (одновременных) уравнений.

Различают несколько видов систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная Y_i (i=1,…,n) рассматривается как функция одного и того же набора факторов X_j (j=1,…,m):

………..

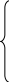
Для нахождения параметров этих моделей используется метод наименьших квадратов.

2. Система совместных (взаимозависимых) уравнений, когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:

_;

_; …………

_;

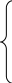Переменные, определяемые внутри системы Y_i (i=1,…,n), называются эндогенными, а переменные, определяемые вне системы X_j (j=1,…,m), – экзогенными. Кроме экзогенных переменных в системе могут быть эндогенные переменные, относящиеся к предыдущим моментам времени (эндогенные переменные с временным лагом). Экзогенные переменные и эндогенные переменные с временным лагом называются предопределенными переменными, так как значения этих переменных известны к текущему моменту времени.

Пример

Рассмотрим систему одновременных уравнений

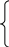, (3.1)

,

где y₁ – спрос-предложение;

y₂ – цена;

х₁ – уровень доходов.

В рассматриваемой модели цена и спрос-предложение рассматриваются как эндогенные переменные, а доход – как экзогенная переменная. Предполагается, что экзогенные переменные определяются вне системы и поэтому не коррелируют со случайными компонентами, отражающим влияние неучтенных факторов. Эндогенные переменные, определяемые из уравнений системы, имеют ненулевую корреляцию со случайными компонентами.

Действительно, разрешая уравнения относительно эндогенных переменных, получим

_,

_.

Отсюда

,

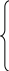. (3.2)

Нетрудно убедиться, что и _.

Таким образом, нарушаются основные предположения регрессионного анализа, что приводит к потере свойств оценок, получаемых методом наименьших квадратов (появляется смещенность и исчезает состоятельность оценок). Поэтому непосредственное применение метода наименьших квадратов приводит к грубым ошибкам.

2. Структурная и приведенная формы экономической модели. Условия индетификации.

Система уравнений (3.1) называется структурной формой модели, а ее коэффициенты – структурными коэффициентами. Система (3.2) называется приведенной формой модели.

Обозначим

; ; ; .

Тогда систему уравнений (3.2) можно переписать в виде

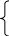_, (3.3)

.

В системе (3.3) объясняющая переменная х₁ является экзогенной переменной и, следовательно, независима со случайными компонентами v₁ и v₂. Метод наименьших квадратов дает состоятельные оценки и .

Очевидно, что . Можно показать, что будет состоятельной оценкой структурного коэффициента .

Такой метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы называется косвенным методом наименьших квадратов.

Вместе с тем, коэффициенты и не могут быть найдены, т. е. они неидентифицируемые.

В общем случае под идентифицируемостью понимают возможность определения структурных коэффициентов уравнений по коэффициентам приведенной формы.

Проблема идентификации – это проблема единственности соответствия между приведенной и структурной формами. Приведенная форма в полном виде имеет nm параметров, а структурная – n(n-1+m) параметров. Ясно, что n(n-1+m) оценок параметров структурной формы в общем случае невозможно получить единственным образом на основе nm параметров приведенной формы.

Необходимое условие идентифицируемости – выполнение следующего правила:

– уравнение идентифицируемое;

– уравнение неидентифицируемое;

– уравнение сверх идентифицируемое,

где Н – число эндогенных переменных в уравнении;

D – число предопределенных переменных системы, отсутствующих в уравнении.

Для сверхидентифицированных уравнений используется двухшаговый метод наименьших квадратов, который заключается в следующем:

– составляют приведенную форму модели и определяют ее параметры обычным МНК;

– выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели;

– обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных расчетные значения эндогенных переменных, стоящих в правой части структурного уравнения.

Пример

Имеется следующая система структурных уравнений

_;

.

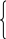Приведенная система уравнений после оценки параметров методом наименьших квадратов имеет вид

_,

_.

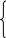Для первого уравнения H=2, D=1 (отсутствует х₄) и , т. е. уравнение является идентифицируемым.

Для второго уравнения H=2, D=1 (отсутствует х₂) и , т. е. уравнение также является идентифицируемым.

Чтобы получить первое структурное уравнение из 1-го приведенного, выразим отсутствующий признак х₄ из 2-го приведенного уравнения:

_.

После подстановки х₄ в первое приведенное уравнение и преобразований, получим

.

Для определения параметров 2-го структурного уравнения выразим отсутствующий во 2-м структурном уравнении фактор х₂ из 1-го приведенного уравнения:

_.

После подстановки х₂ во второе приведенное уравнение, получим

Задание 2

Построить модель вида

_,

,

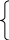рассчитав соответствующие структурные коэффициенты.

Система приведенных уравнений имеет вид

_,

_.

Значения коэффициентов приведены в таблице.

Номер варианта
1	0,006	-0,265	0,003	0,112
2	0,005	-0,308	0,002	0,115
3	0,006	-0,250	0,003	0,128
4	0,005	-0,275	0,002	0,117
5	0,006	-0,283	0,003	0,127
6	0,005	-0,301	0,003	0,110
7	0,006	-0,255	0,002	0,118
8	0,005	-0,315	0,002	0,131
9	0,006	-0,245	0,002	0,113
10	0,005	-0,270	0,003	0,126