5.5. Воспроизведение эталона длины методами интерферометрии

Ко времени проведения первой Генеральной конференции по мерам и весам (1889г., введение эталона метра), А. А. Майкельсон и Э. У. Морли указали на то, что с помощью интерферометра (интерферометра Майкельсона, сокращённо ИМ) возможно сопоставление метра с длиной волны светового излучения. Возможно определение того, сколько длин волн света укладывается на 1 м. В интерферометре Майкельсона пучок света от монохроматического источника Q расщепляется делителем S (полупрозрачное зеркало) на два пучка, один из которых отражается затем от зеркала S1, а другой – от зеркала S2. Эти два пучка объединяются затем в точке В. В точке В может быть установлен какой-либо регистратор световых волн, например фотодиод, измеряющий интенсивность освещения. Мнимое изображение от зеркала S1 на плече зеркала S2 находится в положении S1 '. В положении В имеет место минимум интерференции, если расстояние 2d равно полуцелому числу кратному используемой длины волны света. Путём подсчёта числа минимумов и максимумов при перемещении зеркала S2 можно производить калибровку микрометрического винта М в длинах волн.

В интерферометре используется более или менее протяжённый источник света Q для того, чтобы в месте наблюдения (в точке В) можно было наблюдать систему интерференционных колец Фраунгофера. В центре колец при изменении d наблюдается возникновение новых колец или исчезновение старых. В современных регистрирующих интерферометрах в B помещается фотодиод, подключенный у счётно-регистрирующему электронному устройству. Регистрируя зависимость интенсивности света в центре системы колец от расстояния d, получают так называемые интерферограммы.

Поиски подходящих источников света для оптических методов определения линейных и угловых размеров привели к обнаружению оранжевого излучения атомов ⁸⁶Kr₃₆. Длина волны излучения криптона λ_Kr = 6.05780211·10^-7 м = 605.780211 нм. В природе криптон представлен изотопами с массовыми числами 78 (0.35%), 80 (2.27%), 82 (11.55%), 84 (56.90%) и 86 (17.37%). В оптических средствах измерения используется газообразный криптон, содержащий как минимум 90% 86Kr (в разделительной трубке он поддаётся обогащению до 99,6%). Спин такого дважды чётного ядра (чётный заряд Z = 36 и чётное число нейтронов N = 50) равен нулю. Такому состоянию этого атома соответствует отсутствие сверхтонкой структуры.

5.6. Применение лазерного излучения как стандарта длины волны

Чтобы получить источник света, существенно лучший, чем криптоновая лампа, необходимо добиться достаточной стабильности частоты излучения. Такая стабилизация достигается, если есть возможность производить сравнение интерференционной линии данного излучения с другой очень узкой линией излучения. Создание лазеров открыло возможности для достижения достаточной стабильности частоты излучения и реализации стандартов длины. При этом обеспечиваются такие преимущества, как:

1. Длина когерентности для излучения лазера намного больше (≈10⁴ м), чем для света криптоновой (⁸⁶Kr) лампы (≈0,8 м). Поэтому становятся возможными промеры длины объектов, превышающих 1 м.

2. Большая интенсивность лазера как источника света делает возможным фотоэлектрический подсчёт интерференционных полос. Однако для того, чтобы лазер мог быть использован в качестве стандарта длины волны, необходимо предварительно добиться высокой стабильности длины волны его излучения (Δλ ≈ 10^-10 λ).

5.7. Зависимость измерений линейных размеров от ″выбора″ системы отсчета

Рассмотрим две инерциальные системы K и K'. В систему K' поместим стержень в направлении скорости ее движения. В системе K' стержень покоится и его длина равна l. Свет от источника на левом конце стержня отражается от зеркала на правом конце и возвращается в приемник на левом конце. Тогда длина стержня выражается

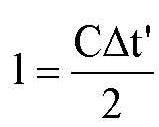^(5.12)

С точки зрения наблюдателя в системе K свет распространяется в течении времени Δt₁ до правого конца и за время Δt₂ возвращается к приемнику. Таким образом

Δt = Δt₁ + Δt₂ . (5.13)

Это время по часам наблюдателя K на первом этапе свет догоняет уходящий правый конец. На втором этапе он движется навстречу левому концу. В этом случае расстояние, пройденное светом в соответствующих направлениях, определяется соотношениями

^(5.14)

и

^(5.15)

где l' – длина стержня относительно системы K. Из равенств (7.18, 7.19) величина Δt

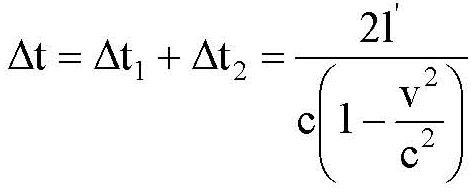^(5.15)

откуда

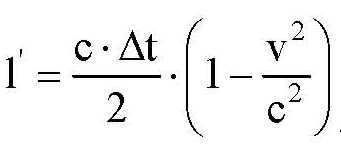. ^(5.16)

С учетом того, что

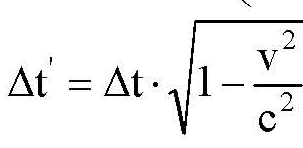
имеем

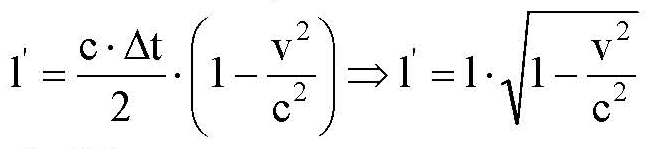^(5.17)

Из выражения (5.17) видно, что длина стержня (размеры тел) в направлении движения сокращаются. Если размер покоящегося тела в некотором направлении равен l, то при движении тела в этом направлении со скоростью v он уменьшается до величины l'<l.