2. Пример расчета переходного процесса в цепи второго порядка операторным методом

Для полученной расчетной схемы (рис. 8)рассчитать переходной процесс для тока в шестой ветви i₆(t) операторным методам и построить график переходного процесса, если  = 0с^-1 т.е. e(t)=100 В, j(t)=2 А,

R=100 Ом, L=0.1 Гн, C=10 мкФ.

Решение

Определяем независимые начальные условия (ННУ), т.е. величины, подчиняющиеся законам коммутации - u_С(0_-) и i_L(0_-). ННУ определяются в схеме до коммутации для момента времени t=0_-.Для определения величины u_С(0_-) и i_L(0_-)необходимо воспользоваться схемой замещения цепи на постоянном токе, в которой емкость заменяется обрывом, индуктивность заменяется проводником и ключ замкнут (рис. 9). Запишем уравнения по законам Кирхгофа. По второму закону Кирхгофа для контуров I, II, III и по первому закону Кирхгофа для узла 1:

(1)

И з системы уравнений (1) напряжение на емкости равно

В.

Ток в индуктивности равен

Таким образом, ННУ равны

u_С(0_-) = U_C =0 В; i_L(0_-) = 1 A.

Н енулевое начальное напряжение на емкости учитываем источником ЭДС E_С(р), а ток в индуктивности - E_L(р) (рис .10). Для цепи послекоммутационной конфигурации составляем эквивалентную операторную схему замещения (рис. 11).

В операторной схеме замещения параметры схемы имеют следующие значения:

; ; ;

где по закону коммутации и .

Полученная операторная схема замещения (рис. 11) является сложной схемой, поэтому для нахождения операторного изображения тока в шестой ветви I₆(p) воспользуемся методом контурных токов. Для указанных контуров в схеме рис. 11 запишем систему уравнений:

Подставляя значения в полученную систему, получим:

(2)

Так как операторное изображение тока , то выразим из системы (2) операторное изображение контурного тока по правилу Крамера:

После упрощения получим:

Таким образом, операторное выражение искомого тока после подставки числовых значения имеет вид

(3)

Осуществляем переход от изображения к оригиналу i₆(t) по теореме разложения. Определим корни характеристического уравнения из условия .

Один корень равен нулю, а остальные найдем из уравнения

или

.

При решении полученного уравнения корни имеют вид

.

Так как есть нулевой корень (р=0) и комплексно-сопряженные корни р_1,2, то используем следующую форму записи теоремы разложения:

где F₁(0) – значение полинома числителя при р=0;

F₂(0) – значение полинома знаменателя при р=0;

- корень характеристического уравнения, который определяется из условия F₂(р)=0;

F₁(р₁) – значение полинома числителя при р=р₁;

- производная полинома знаменателя по р с подстановкой корня р=р_1.

Находим значения величен, входящих в состав теоремы разложения:

F₁(0)=100; F₂(0)=200;

.

Подставляем найденные значения в теорему наложения и получаем

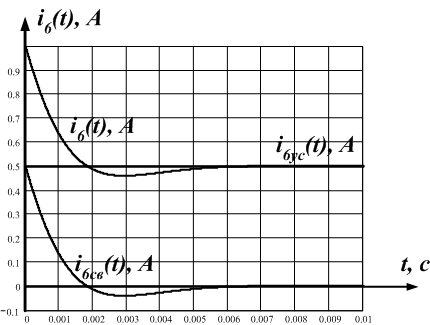
График для найденного значения тока i₆(t) показан на графике рис.12.

i_L(t), A

Рис. 12

Второй уровень

Применяя программу моделирования и анализа электротехнических схем ELECTRONICS WORKBENCH, необходимо:

1) собрать заданную схему в ELECTRONICS WORKBENCH (рис. 13) с исходными данными для классического метода, снять осциллограмму для искомой величины (ток или напряжение) (рис.14 и рис. 15) и сравнить с результатами расчета, выполненными классическим методом (рис. 16).

2) включить в собранную схему в ELECTRONICS WORKBENCH (рис. 17) постоянные источники как для операторного метода и снять осциллограмму для искомой величины (тока или напряжения) (рис.18 и рис.19) и сравнить с результатами расчета, выполненными операторным методом (рис. 20).

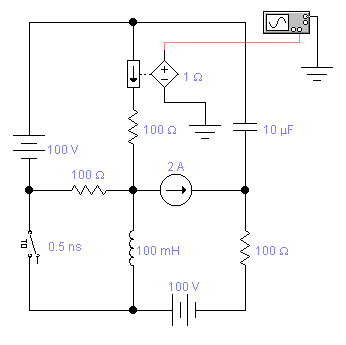
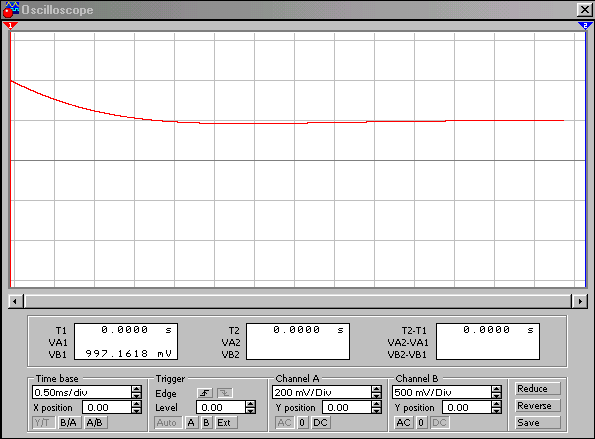
Рис. 17

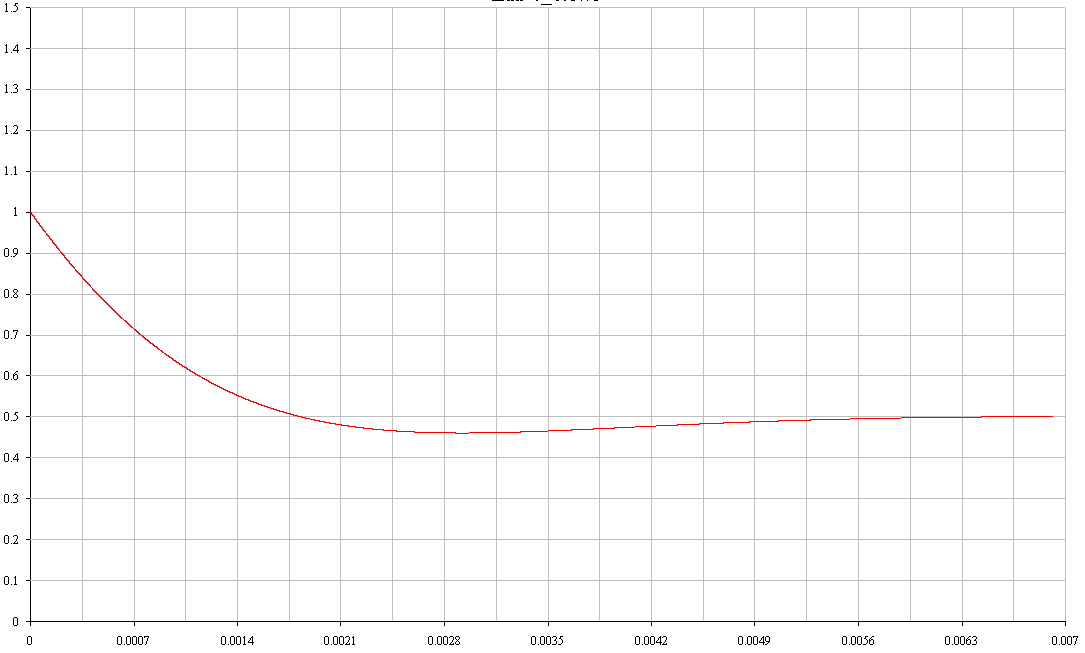
Рис. 18

2) составить систему дифференциальных уравнений и решить ее, используя функцию Rkadapt(y, x1, x2, npoints, D) MathCad (рис.24), построить графики переходных процессов для тока в индуктивности, тока i₆(t) (рис. 25) и напряжения на емкости (рис.26), если Е=100 В, J=2 A.