1. Пример расчета переходного процесса в цепи второго порядка классическим методом

Исходные данные для варианта № 000 приведены в табл. 2, а получаемая расчетная схема приведена на рис. 2.

Таблица 2

Вариант	Номер ветви								Найти
№	1	2	3	4	5	6	7	8
000	e(t)	С	e(t),R	КР	R	R	j(t)	L		i6(t)

Н айти закон изменения тока в шестой ветви i₆(t) (рис. 3) при размыкания ключа классическим методом, еслиe(t)=100 Cos(1000t);j(t)=1 Cos(1000t);R=100 Ом, L=0.1 Гн; C=10 мкФ.

Решение

В схеме после коммутации (рис. 2) находится одна емкость и одна индуктивность. Следовательно, цепь второго порядка.

Запишем решение дифференциального уравнения в общем виде для тока в шестой ветви:

i₆(t) = i_6ус(t)+ i_6св(t). (1)

О пределим i_6ус(t) в схеме после коммутации. Так как источники гармонического тока, то перейдем к комплексной схеме замещения и определим её параметры (рис. 3):

Z_L=jwL=j100 Ом; Z_R=R=100 Ом;

Z_С= – j = – j100 Ом;

;

.

Так схема сложная (рис. 3), то для нахождения комплексного действующего значения тока в шестой ветви ( ) воспользуемся методом контурных токов. Запишем уравнения по методу контурных токов для указанных контуров:

или

Подставим численные значения и решим полученную систему относительно контурных токов:

или:

Откуда А, А.

Следовательно, А.

Переходим во временную область для определения мгновенного значения тока i_6ус(t):

(2)

Характеристическое уравнение составляется из условия Zвх(р)=0. Чтобы получить характеристическое уравнение, необходимо в схеме после коммутации положить источники равными нулю (Е=0, J=0) и записать уравнение для входного комплексного сопротивления Zвх(j) относительно любой ветви (рис. 4).

Zвх(j)= .

Полагаем, что j=р и Zвх(р)=0, получаем характеристическое уравнение

или p²LC+рСRэ+1=0, (3)

где Ом.

Решаем квадратное уравнение (3):

; или .

Следовательно, корни характеристического уравнения будет иметь значение

Так как корни характеристического уравнения комплексно-сопряженные, то свободная составляющая i_6св(t) искомого тока i₆(t) имеет вид

i_6св(t)= ,

где  = 750,

_СВ= 250 .

Следовательно, уравнение (1) будет иметь вид

. (4)

Для определения постоянных интегрирования А₁и А₂ необходимо записать уравнение (4) и ее первую производную для момента времени t=0_+,

так как установившееся значение тока

,

то

или

(5)

где i₆(0₊) и – начальные условия.

Т аким образом, чтобы найти постоянные интегрирования А₁и А_2, необходимо знать начальные условия i₆(0₊) и

Начальные условия делятся на независимые начальные условия (ННУ) и зависимые начальные условия (ЗНУ). К независимым начальным условия относятся величины, подчиняющиеся законам коммутации, т.е. u_С(0_-) и i_L(0_-). ННУ определяются в схеме до коммутации для момента времени t=0_-.Для определения этих величин u_С(0_-) иi_L(0_-) необходимо воспользоваться методом комплексных амплитуд, так как источники гармонические. Комплексная схема замещения до коммутации показана на рис. 5.

Так схема сложная (рис. 5), то для нахождения комплексного действующего значения тока и напряжения воспользуемся методом контурных токов. Запишем уравнения по методу контурных токов для указанных контуров:

Так как , то уравнения можно записать в следующем виде:

Подставляя в полученные уравнения численное значение данных и сокращая на 100, получим систему уравнений(8):

(6)

В результате решения системы уравнений (6) получаем:

Таким образом, ток индуктивности равен А, а напряжение на емкости равно В.

Переходим во временную область для определения мгновенного значения тока i_L(t) и U_C(t):

,

.

Следовательно, ННУ u_С(0_-) иi_L(0_-) для момента времени t=0_-

равны

А;

В.

К зависимым начальным условия относятся величины, не подчиняющиеся законам коммутации. В данной задаче i₆(0₊) и - этоЗНУ и они определяется в схеме после коммутации в момент времени t=0₊. Для нахождения ЗНУ воспользуемся схемой (рис. 6) замещения для цепи после коммутации, в которой емкость заменим источником ЭДС величиной u_C(t), а индуктивность – источником тока со значением i_L(t)

В полученной схеме замещения (рис. 6) определим вначале ток i₆(t) используя законы Кирхгофа.

Для 0 узла запишем первый закон Кирхгофа:

i₁(t) - i₆(t) + j₇(t) + i_L(t)=0. (7)

Для контура I запишем второй закон Кирхгофа

R₆ i₆(t)+ R₅ i₁(t) = e₁(t). (8)

Из уравнения (8) значение тока i₁(t) подставим в уравнение (7) и определяем ток i₆(t)

(9)

Чтобы найти величину , необходимо продифференцировать уравнение (9), т.е.

(10)

где

;

;

.

Значение u_L(t) можно найти из уравнения, записанного по второму закону Кирхгофа для II контура в схеме, изображенной на рис. 6:

-R₆ i₆(t) - R₃ i_L(t) - u_L(t)= e₃(t)- u_C(t).

Откуда

u_L(t)=- e₃(t)+ u_C(t) -R₆ i₆(t) - R₃ i_L(t). (11)

Теперь можно найти ЗНУ i₆(0₊) и , если в уравнения (9), (10) и (11) подставить значение времени t=0₊.

По найденным начальным условиям i₆(0₊) и из системы уравнений (5) определяем постоянные интегрирования А₁и А₂:

откуда

Найденные численные значения для величинi_6ус(t), _св ,, А₁и А₂подставляем в уравнение (4) и записываем ответ в виде:

Для построения графика уравнение (5) удобнее записать в виде

,

где ; .

Таким образом, А.

График переходного процесса изображен на 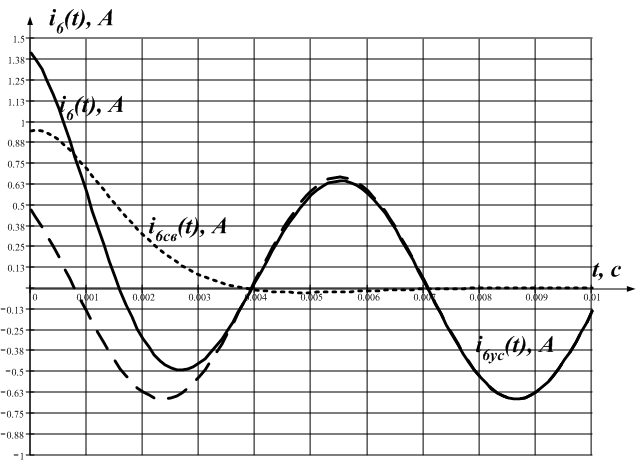рис. 7.

Рис. 7