Лекция 2. Непрерывные отображения и их свойства. Гомеоморфизм
План. Непрерывное
отображение топологических пространств.
Свойства непрерывных отображений.
Категория 
.
Гомеоморфизм. Гомеоморфность топологических
пространств как отношение эквивалентности.
Локальный гомеоморфизм.
Цель лекции - ввести понятие непрерывного отображения, установить его связь с понятием непрерывной числовой функции, дать строгие доказательства привычных свойств непрерывных отображений, привести пример категории, исследовать понятие гомеоморфизма и дать наглядные примеры гомеоморфных и локально гомеоморфных пространств.
Непрерывным называется
отображение 
топологических
пространств, при котором выполнено
следующее свойство: прообраз 
каждого
открытого в пространстве 
подмножества 
является
открытым подмножеством в пространстве 
.
Равносильное определение: непрерывным называется отображение, при котором прообразы замкнутых множеств замкнуты.
Упражнение. Проверьте эквивалентность двух определений непрерывного отображения.
Также нам потребуется определение отображения, непрерывного в точке.
Отображение
топологических
пространств называется непрерывным
в точке 
если
для всякой окрестности 
точки 
существует
такая окрестность 
точки
,
что 
Сравним
это общее определение с привычным
определением непрерывной в точке
числовой функции из курса математического
анализа. Функция 
непрерывна
в точке 
,
если выполнено условие:
Числовая
прямая является метрическим пространством
с метрикой вида 
поэтому,
выбрав окрестности точек в виде открытых
шаров (которые в данном случае являются
открытыми интервалами), получим
определение функции, непрерывной в
точке.
Можно доказать, что отображение топологических пространств непрерывно тогда и только тогда, когда оно непрерывно в каждой точке.
В
самом деле, если отображение 
непрерывно,
а
-
окрестность точки 
,
то ее прообраз 
является
окрестностью точки 
,
причем 
.
Обратно, если отображение 
непрерывно
в каждой точке и
-
открытое множество в пространстве
,
то каждая точка множества
обладает
окрестностью, образ которой принадлежит
множеству
.
Таким образом, прообраз
является
объединением открытых подмножеств,
следовательно, он открыт в пространстве
.
Теперь обратимся к простейшим свойствам непрерывных отображений топологических пространств.
Теорема 1. Тождественное отображение топологического пространства в себя непрерывно.
Для
доказательства рассмотрим тождественное
отображение 
,
переводящее каждую точку пространства
в
себя. Пусть 
-
открытое подмножество, тогда, очевидно,
и,
следовательно, 
,
что и требовалось.
Теорема
2. Для
любого пространства 
постоянное
отображение 
,
где 
-
одноточечное пространство, непрерывно.
Доказать это свойство читателю предлагается в качестве упражнения.
Теорема 3. Отображение вложения подпространства в топологическое пространство непрерывно.
Действительно,
рассмотрим вложение подпространства 
,
и пусть 
-
произвольное открытое в
подмножество.
Тогда 
-
открытое в
подмножество,
согласно определению топологии
подпространства.
К доказательству теоремы о композиции
Теорема 4. Композиция непрерывных отображений топологических пространств непрерывна.
Для
доказательства рассмотрим непрерывные
отображения топологических
пространств 
и 
и
их композицию
Пусть
-
произвольное открытое подмножество
пространства 
.
Его прообраз относительно композиции 
равен
По
определению непрерывного отображения,
подмножество 
открыто
в пространстве
,
а подмножество 
открыто
в пространстве
.
Совокупность
подмножеств 
называется покрытием
множества
,
если 
.
Здесь символом 
обозначено
множество индексов, нумерующих элементы
покрытия
,
при этом мощность покрытия может быть
счетной (конечной или бесконечной) или
несчетной. Покрытие топологического
пространства
называют открытым,
если все составляющие его
подмножества
открыты
в
.
Топологическое пространство
называется компактным,
если всякое его открытое покрытие
содержит конечное покрытие.
Ясно,
что конечное множество, наделенное
дискретной топологией, компактно, а
бесконечное множество с дискретной
топологией некомпактно. Менее тривиальный
пример некомпактного топологического
пространства - хорошо знакомое читателю
евклидово вещественное пространство 
,
топология которого задана с помощью
метрики
Для
доказательства некомпактности
пространства
достаточно
указать одно его открытое покрытие,
которое не содержит конечного подпокрытия.
Такое покрытие образуют открытые шары
радиуса 
,
центры которых расположены во всех
точках с целочисленными координатами.
Действительно, такие шары образуют
покрытие, причем любой конечный набор
таких шаров покрытия не образует.
Теорема 5. Пусть - сюръективное непрерывное отображение топологических пространств. Если - компактное топологическое пространство, то и компактно.
Действительно,
пусть 
-
открытое покрытие пространства
.
Множества
для 
составляют
открытое покрытие пространства
,
и если 
-
его конечное подпокрытие, то 
-
конечное подпокрытие покрытия
пространства
.
Теперь обратимся к понятию категории.
Категория состоит
из двух классов - класса
объектов и класса
морфизмов, -
удовлетворяющих требованиям :
1.
Для каждой пары объектов 
определено
множество 
морфизмов
из
в
;
2.
Для каждой тройки объектов 
определено
отображение
ставящее
в соответствие двум
морфизмам
и 
их композицию 
.
3.
Множества
и
композиция морфизмов удовлетворяют
аксиомам:
а)
композиция ассоциативна: для каждой
тройки морфизмов
имеет
место равенство 
;
б)
для каждого объекта
существует тождественный
морфизм 
такой,
что любых объектов 
и 
и
для любых морфизмов 
и 
имеют
место равенства
, 
;
в)
если пары 
и 
различны,
то пересечение множеств
и 
пусто.
Рассматривая в качестве объектов все топологические пространства (то есть все множества со всевозможными топологиями на них) и в качестве морфизмов все возможные непрерывные отображения между топологическими пространствами, получим категорию топологических пространств (и непрерывных отображений). Читателю также знакомы категории множеств (и их отображений), векторных пространств (и их линейных отображений), групп (и их гомоморфизмов) и колец (и их гомоморфизмов).
Отображение
топологических
пространств называется гомеоморфизмом,
если оно
1) непрерывно,
2)
взаимно однозначно,
3) обладает
непрерывным двусторонним обратным
отображением 
,
то есть таким непрерывным отображением 
,
что 
, 
.
Для любого неодноточечного пространства постоянное отображение не является гомеоморфизмом (оно не взаимно однозначно и тем более не обратимо).
Из
непрерывности обратимого отображения
не
следует непрерывность обратного
отображения
.
Пусть 
-
тождественное отображение непустого
множества 
наделенного
дискретной топологией, в то же множество
,
наделенное любой другой топологией.
Такое отображение непрерывно (проверьте!).
Обратное отображение
не
является непрерывным.
Приведем примеры гомеоморфных топологических пространств, известных из других курсов геометрии.
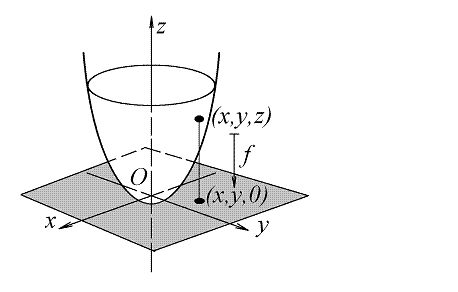
Пример гомеоморфизма
1.
Параболоид вращения, заданный в трехмерном
евклидовом пространстве уравнением 
,
гомеоморфен евклидовой плоскости.
Для
построения отображения, осуществляющего
гомеоморфизм, будем считать, что плоскость
задана уравнением 
(рис.
4). Отображение
-
проектирование параболоида на
плоскость
параллельно
координатной оси 
-
задается в координатах следующим
образом:
Обратное отображение плоскости на параболоид имеет вид:
Оба отображения заданы непрерывными функциями и, следовательно, непрерывны, что и доказывает гомеоморфизм.
2. Трехосный эллипсоид гомеоморфен сфере.
Каноническое уравнение трехосного эллипсоида имеет вид:
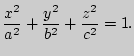
Уравнение
сферы с центром в начале координат: 
Отображение
эллипсоида на сферу, осуществляющее
гомеоморфизм, задается в координатах
следующим образом:
(
)
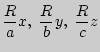Гомеоморфизм
устанавливает взаимно однозначное
соответствие между открытыми подмножествами
гомеоморфных топологических пространств.
В самом деле, в силу непрерывности
отображения 
,
осуществляющего гомеоморфизм, прообраз
любого открытого в
множества
открыт, то есть
непрерывно
Аналогично, в силу непрерывности обратного отображения прообраз при отображении любого открытого в множества также открыт:
непрерывно
Доказанное означает, что если некоторое топологическое утверждение верно для одного из двух гомеоморфных топологических пространств, то такое же утверждение верно для другого. Гомеоморфные пространства топологически неразличимы, поэтому о них говорят, что они имеют один топологический тип.
Отношение гомеоморфности в классе топологических пространств рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности (докажите!)
Отображение
топологических
пространств называется локальным
гомеоморфизмом, если
у каждой точки 
пространства
имеется
такая окрестность 
,
что ограничение
отображения
осуществляет
гомеоморфизм окрестности
на
ее образ 
.
При этом пространства
и
называются локально
гомеоморфными.
Топологические пространства могут быть негомеоморфными, но локально гомеоморфными. Таковы, например, тор (компактное пространство) и евклидова плоскость (некомпактное пространство.)
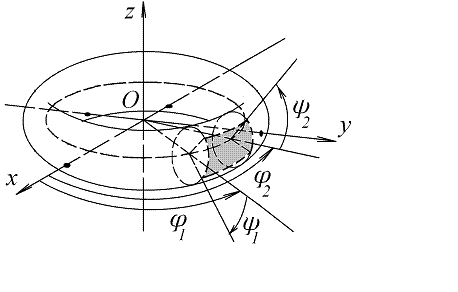
Пример локального гомеоморфизма
Действительно,
представим тор как поверхность,
образованную вращением окружности
около оси, лежащей в плоскости окружности
и не пересекающей ее. Тогда точки тора
снабжаются угловыми координатами,
например, так, как показано на рисунке
5. Положительные углы 
отсчитываются
от положительного направления оси 
в
сторону положительного направления
оси 
,
положительные углы 
отсчитываются
от плоскости
в
сторону положительного направления
оси
.
Тогда область, соответствующая значениям
угловых координат 
и
,
гомеоморфна прямоугольнику (рис. 6).
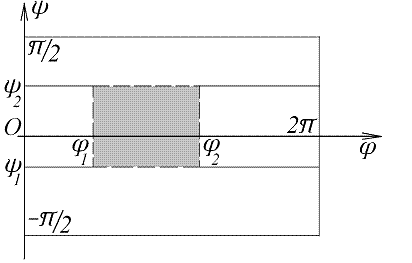
Пример локального гомеоморфизма
Локальные
гомеоморфизмы чрезвычайно важны в
дифференциальной геометрии, а точнее
- при построении дифференциального и
интегрального исчислений на геометрических
объектах, отличных от евклидова
пространства
(например,
прямой 
или
плоскости 
)
Непреры́вное отображе́ние или непрерывная функция в математике — это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений.
Наиболее общее определение формулируется для отображений топологических пространств: непрерывным считается отображение, при котором прообраз всякого открытого множества открыт. Непрерывность отображений других типов пространств — метрических, нормированных и т. п. пространств — является непосредственным следствием общего (топологического) определения, но формулируется с использованием структур, заданных в соответствующих пространствах — метрики, нормы и т. д.
В математическом анализе и комплексном анализе, где рассматриваются числовые функции и их обобщения на случай многомерных пространств, непрерывность функции вводится на языкепределов: такие определения непрерывности были исторически первыми и послужили основой для формирования общего понятия.
Существование непрерывных отображений между пространствами, позволяет «переносить» свойства одного пространства в другое: например, непрерывный образ компактного пространстватакже является компактным.
Непрерывное отображение, которое обладает обратным и также непрерывным отображением, называется гомеоморфизмом. Гомеоморфизм порождает на классе топологических пространствотношение эквивалентности; пространства, гомеоморфные друг другу, обладают одними и теми же топологическими свойствами, а сами свойства, которые сохраняются при гомеоморфизмах, называются топологическими инвариантами.
Содержание
|
Определения
Наиболее общее определение даётся в топологии.
Непрерывность в топологических пространствах
Отображение топологического пространства в топологическое пространство называется непрерывным, если прообраз любого открытого множества открыт, то есть:
.
Непрерывность на подпространстве
Если рассмотреть некоторое подмножество множества , то на этом множестве, естественным образом, индуцируется топология , которую составляют всевозможные пересечения множества с множествами, входящими в топологию .
Отображение , непрерывное на множестве , будет непрерывным на любом его подмножестве в смысле индуцированной на нём топологии.
Непрерывность в точке
Непрерывность в точке формулируется на языке окрестностей и связывает систему окрестностей точки области определения с системой окрестностей соответствующей ей точки области значений.
Отображение называется непрерывным в точке , если для любой окрестности точки найдется такая окрестность точки , что .
Отображение, непрерывное на некотором множестве, будет непрерывным в каждой точке данного множества.[1]
Эквивалентные определения
Следующие ниже формулировки эквивалентны:
прообраз всякого открытого множества открыт;
прообраз всякого замкнутого множества замкнут;
прообраз каждой окрестности точки области значений отображения является окрестностью соответствующей точки области определения;
предел значений последовательности точек области определения, сходящейся к некоторой точке, существует и в точности равен значению функции в данной точке;
образ замыкания любого множества содержится в замыкании образа этого множества;
замыкание прообраза любого множества содержится в прообразе замыкания.
Таким образом, каждая из этих формулировок может быть использована в качестве определения непрерывности отображения.
Непрерывность в метрических и нормированных пространствах
В метрических пространствах топология задается семейством открытых шаров разных «радиусов», определяемых метрикой, поэтому общее определение формулируется в терминах этой метрики ("эпсилон-дельта" - определение):
Отображение метрического пространства в метрическое пространство называется непрерывным в точке , если для всякого существует , что для всякого , такого, что , выполняется неравенство: .
Для линейных нормированных пространств (включая, гильбертовы и конечномерное евклидовы пространства) метрика задается нормой, поэтому то же определение дается в терминах нормы.
Пусть, отображение между нормированными пространствами с нормами и соответственно. Функция непрерывна в точке , если для любого числа найдётся такое число , что для всех точек , таких что выполнено неравенство ,
Метрические пространства (а значит и нормированные пространства) удовлетворяют первой аксиоме счетности, поэтому данное определение эквивалентно определению секвенциальной непрерывности.
Непрерывные функции (функционалы)
В случае числовой оси нормой обычно является модуль числа, поэтому определение непрерывности функционала (или .), где - произвольное топологическое пространство, следующее:
Фунционал , называется непрерывным в точке , если для любого найдется окрестность этой точки, такая, что выполнено условие .
Множество непрерывных на функционалов (функций) принято обозначать . Частным случаем непрерывных функционалов являются непрерывные функции числового аргумента.
Непрерывная числовая функция
Основная статья: Непрерывная функция
Пусть, . (или .). Функция непрерывна в точке , если для любого числа найдётся такое число , что для всех точек условие влечет .
Другими словами, функция непрерывна в точке , предельной для множества , если она имеет предел в данной точке и этот предел совпадает со значением функции в данной точке:
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества. В этом случае говорят, что функция класса и пишут: или, подробнее, .
Свойства непрерывных отображений
Полный прообраз любого открытого (замкнутого) множества при непрерывном отображении — открытое (замкнутое) множество
Образ компактного множества при непрерывном отображении — компактное множество.
Непрерывная числовая функция на компактном множестве ограничена и достигает своих верхней и нижней граней. Это свойство следует из предыдущего.
Образ связного множества при непрерывном отображении - связное множество.
(Теорема Титце.) Любая вещественнозначная непрерывная функция, определённая на замкнутом подмножестве нормального пространства может быть продолжена до непрерывной функции на всё пространство.
Сумма, разность и композиция непрерывных отображений также являются непрерывными отображениями.
Из непрерывности линейного отображения одного линейного топологического пространства в другое следует его ограниченность. В случае нормированных пространств непрерывность линейного отображения эквивалентна ограниченности.
Теорема Стоуна-Вейерштрасса (обобщение классической теоремы Вейерштрасса). Пусть - пространство непрерывных функций на компактном хаусдорфовом топологическом пространстве . Пусть - подмножество , содержащее константы, замкнутое относительно композиции и линейной комбинации функций, а также содержащее пределы своих равномерно сходящихся последовательностей функций. В таком случае тогда и только тогда, когда , существует , такая что .