
- •Министерство образования и науки российской федерации
- •Национальный исследовательский томский политехнический университет
- •1 Задания и сходные данные для расчета
- •2 Расчёт переходной характеристики для цепи rl
- •2.1 Преобразования Лапласа
- •2.2 Численный метод
- •2.4 Применение интегральной оценки погрешности
- •3 Расчёт переходной характеристики для цепи rlс (фнч)
- •3.1 Преобразования Лапласа
- •3.2 Численный метод
- •3.4 Применение интегральной оценки погрешности
- •Список литературы
- •Контрольный вопрос
3 Расчёт переходной характеристики для цепи rlс (фнч)
Для цепи RLC необходимо составить систему дифференциальных уравнений, описывающих состояние ФНЧ.
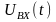 – входное
напряжение;
– входное
напряжение;
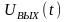 –
выходное
напряжение;
–
выходное
напряжение;
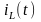 –
ток
катушки индуктивности;
–
ток
катушки индуктивности;
 – ток
конденсатора;
– ток
конденсатора;
 –
ток
нагрузки.
–
ток
нагрузки.
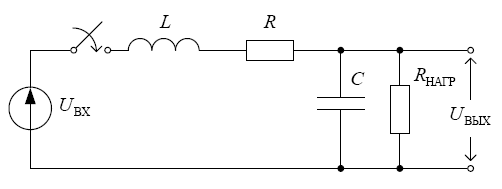
Рисунок 6 – Схема ФНЧ
По второму закону Кирхгофа входное напряжение уравновешивается как
 ,
(7)
,
(7)
Согласно первому закону Кирхгофа ток катушки индуктивности расщепляется на ток конденсатора и ток нагрузки:
 ,
(8)
,
(8)
Известно, что ток конденсатора определяется как
 ,
(9)
,
(9)
а ток нагрузки по закону Ома выразим как
 ,
(10)
,
(10)
Система дифференциальных уравнений, описывающих состояние ФНЧ с учётом (7) – (10), выглядит следующим образом:
 (11)
(11)
Все дальнейшие расчеты проводим анологично как для цепи RL
3.1 Преобразования Лапласа
Применим к выражению (11) прямое преобразование Лапласа, получим систему алгебраических уравнений в изображениях и проведём алгебраические преобразования:
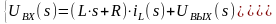 (12)
(12)
где s – оператор Лапласа.
Подставим второе уравнение системы (6) в первое и проведём алгебраические преобразования:
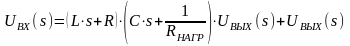 ,
,
 .
(13)
.
(13)
Операторной
передаточной функцией ФНЧ
 называется
отношение изображение выходного сигнала
ко
входному
:
называется
отношение изображение выходного сигнала
ко
входному
:
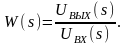 (14)
(14)
С учётом (13) и (14) запишем выражение для операторной передаточной функции ФНЧ:
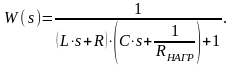 (15)
(15)
Для облегчения расчётов воспользуемся MathCAD:
![]()
![]()
![]()
![]()
![]()
![]()
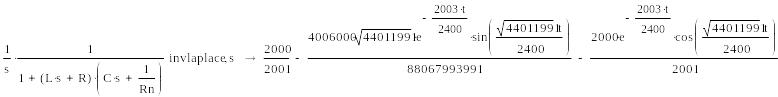
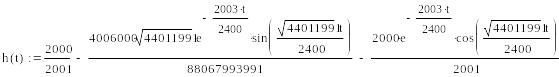
![]()
![]()
![]()
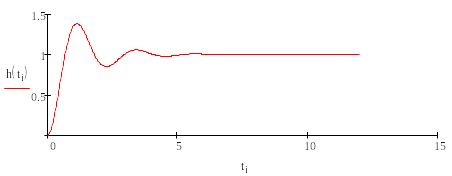
Рисунок 7
3.2 Численный метод
Воспользуемся методом Эйлера для решения системы уравнения, для этого преобразуем уравнение (11) к нормальной форме Коши:
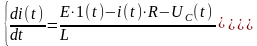 (16)
(16)
Аналогично решим в программе MathCAD
![]()
![]()
![]()
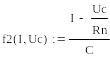
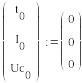
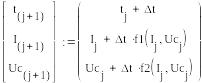
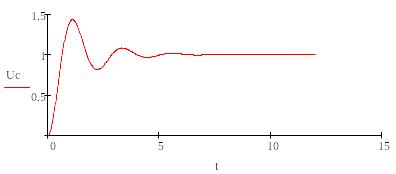
Рисунок 8
3.3 Z-преобразования
Воспользуемся MathCAD для дальнейших преобразований:
![]()
![]()

![]()
![]()
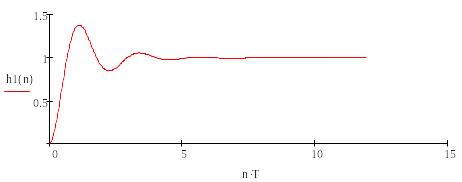
Рисунок 9
3.4 Применение интегральной оценки погрешности
В связи с колебательным переходным процессом применяют такие интегральные оценки, в которой знакопеременность подынтегральной функции устранена. Таким свойством обладает квадратичный интегральный критерий.
(17)
Представим, что переходная функция рассматриваемой динамической системы, полученная с применением преобразования Лапласа, является эталонной XЭ(t). Оценим качество переходного процесса с применением интегрального критерия. Поскольку из рисунков 10 и 11 видно, что переходный процесс колебательный (периодический), воспользуемся линейным интегральным критерием оценки I2.
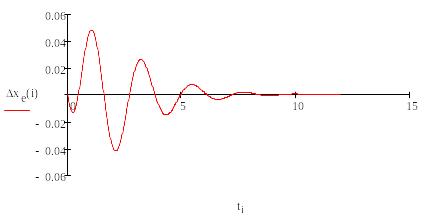
Рисунок
10 – График функции ошибки
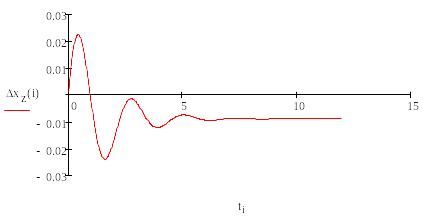
Рисунок
11 – График функции ошибки
Однако при применении численных методов и Z-преобразований полученные функции не являются непрерывными, что не позволяет провести их интегрирование, для оценки необходимо применить численное интегрирование. Воспользуемся методом трапеции [3], тогда квадратичный интегральный критерий (17) преобразуется к виду:
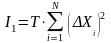
Оценим качество переходных процессов относительно h(t) методом трапеции, воспользуемся MathCAD.
|
|
Вывод
В данной лабораторной работе научился применять различные методы расчета переходных процессов, а также рассчитывать интегральную оценку качества переходного процесса
Наиболее точным расчетом переходных процессов является расчет по Лапласу, но не всегда входной сигнал является непрерывным. В таких случаях применяют Z-преобразования.
