Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный исследовательский томский политехнический университет

Институт – Энергетический институт

Направление – Энергосбережение и энергоэффективность

Кафедра – Электрические сети и электротехника

«Переходные процессы в дискретных системах и интегральные оценки качества»

^{Наименование лабораторной работы}

Отчет по лабораторной работе № 5

по курсу «Дополнительные главы математики»

^{Наименование учебной дисциплины}

Вариант №27

Выполнил студент гр 5АМ22 ________Д.А. Умутбеков

^{Подпись Дата И.О.Фамилия}

Проверил доцент______ _______ _________ А.С. Глазырин

^{должность Подпись Дата И.О.Фамилия}

Томск – 2012

Содержание

Цель работы…………………………………………………………...……3

1 Задания и сходные данные для расчета ………………………………. 3

2 Расчёт переходной характеристики для цепи RL…………………...….4

2.1 Преобразования Лапласа……………………………………………5

2.2 Численный метод…………………………………………..………..6

2.3 Z-преобразование……………………………………………………7

2.4 Применение интегральной оценки погрешности……………..…..8

3 Расчёт переходной характеристики для цепи RLС (ФНЧ)……….….11

3.1 Преобразования Лапласа…………………………………………..12

3.2 Численный метод…………………………………………….…….13

3.3 Z-преобразование…………………………………………………..14

3.4 Применение интегральной оценки погрешности…………….…..15

Вывод………………………………………………………………………17

Список литературы…………………………………………………….....18

Ответы на контрольные вопросы……………………………………...…19

Цель работы

1.Научиться применять различные способы расчёта переходной характеристики динамической системы

2.Научиться рассчитывать интегральную оценку качества переходного процесса

1 Задания и сходные данные для расчета

Задача 1. Рассчитать переходный процесс для RL-цепи первого порядка тремя представленными способами. Провести интегральную оценку погрешности относительно переходной функции полученной по Лапласу. Данные для задания представлены в таблице 1.

Задача 2. Рассчитать переходный процесс для RLC-цепи второго порядка тремя представленными способами. Провести интегральную оценку погрешности относительно переходной функции полученной по Лапласу. Данные для задания представлены в таблице 2 при R=1 Ом.

Таблица 1

Вариант	R, Ом	L, Гн	Метод численного интегрирования
27	60	0,1	Трапеции

Таблица 2

Вариант	L, Гн	С, мкФ	№ Вопроса
27	400	300	2

2 Расчёт переходной характеристики для цепи rl

Найдём величину изменения тока при переходном процессе в цепи первого порядка рисунок 1

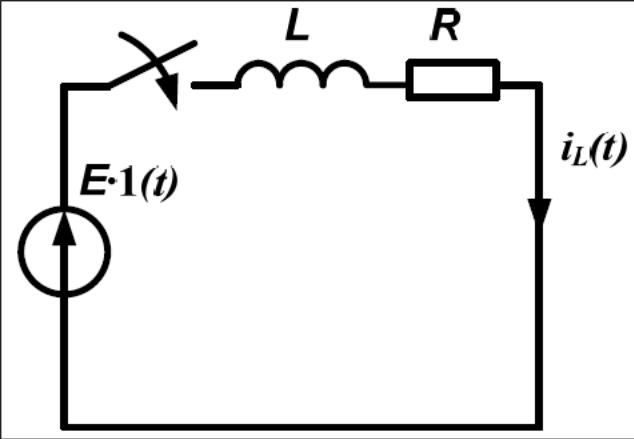
Рисунок 1 – Схема коммутации RL-цепи на источник постоянного напряжения

Процессы, протекающие в цепи при замыкании ключа, описываются дифференциальным уравнением 1 порядка, составленным по второму закону Кирхгофа:

₍₁₎

Полученное дифференциальное уравнение (1), позволяет произвести расчёт переходного процесса для заданной цепи.

Для построения графика необходимо определить время переходного процесса. Для этого найдём корень характеристического уравнения λ:

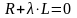
преобразовав выражение получим:

Постоянная времени равна:

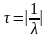
_{Интервалы дискретизации в каждом из методов буде одинаковы и определяется по формуле:}

где N – количество отсчётов на которые разбивается исследуемый интервал переходного процесса.