Сила Архимеда в неинерциальной системе отсчета.
1. Ускорение a системы направлено вертикально вниз.
Т.к. гидростатическое давление в этом случае вычисляется по формуле (5.1.4): , то сила Архимеда равна
(5.2.2)
В невесомости сила Архимеда отсутствует:FA = 0.
Если ускорение a системы направлено вертикально вверх, то
(5.2.3)
2. Ускорение a системы направлено горизонтально. (рис. 5.2.4)
Уровень жидкости
в этом случае наклонен под углом :
.
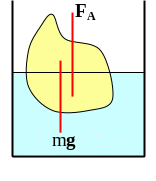
Рис. 5.2.4. Рис. 5.2.5.
Получим формулу для силы Архимеда. Мысленно удалим тело и заполним образовавшуюся полость жидкостью. Эта жидкость, массой mж, будет двигаться с ускорением a. Тогда
.
.
(5.2.4)
Направление выталкивающей силы совпадает с вектором a – g, т.е. сила Архимеда перпендикулярна поверхности жидкости. Формула (5.2.4) позволяет найти силу Архимеда в случае произвольного направления вектора a. Если вектор a – горизонтален, то
.
(5.2.5)
Условия плавания. (рис. 5.2.5)
1. Тело тонет, если
,
т.е. средняя плотность тела больше
плотности жидкости:
.
2. Тело всплывает,
если
,
т.е. средняя плотность тела меньше
плотности жидкости:
.
Положение равновесия плавающего тела
- устойчивое равновесие. При этом
выталкивающая сила равна
,
(5.2.6)
где Vпогр. – объем погруженной части тела.
Устойчивость плавания корабля.
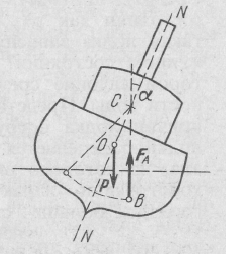
Рис. 5.2.6.
Для строительства кораблей большое значение имеет вопрос устойчивости его плавания. На рис. 5.2.6 изображен корабль, накрененный на некоторый угол от вертикального положения. При этом центр тяжести вытесненной кораблем воды в наклоненном положении (точка приложения выталкивающей силы) находится в точке B, смещенной из плоскости симметрии корабля NN в ту же сторону, куда накренился корабль. Проведем через точку B вертикаль, которая представляет собой линию действия выталкивающей силы. Точка C пересечения линии действия выталкивающей силы наклоненного корабля с плоскостью симметрии корабля называется метацентром.
Если метацентр лежит выше центра тяжести корабля O, то момент выталкивающей силы относительно центра тяжести корабля стремится возвратить корабль в вертикальное положение, т.е. корабль плавает устойчиво.
Если же метацентр лежит ниже центра тяжести корабля O, то плавание корабля в вертикальном положении будет неустойчивым.