§4. Пробой

Если после насыщения разность потенциалов на электродах продолжает увеличиваться, то наступает стадия, на которой ток снова растет.

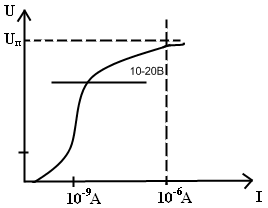
Характер этого возрастания зависит от давления газа, однако, для любых давлений с увеличением U ток I растет с возрастающей скоростью и наконец, достигается напряжения U_п, при котором значение тока I лимитируется только сопротивлением внешней цепи.

Вольтамперная характеристика до этой точки показана на рисунке. Величину U_п называют напряжением пробоя. Его значение зависит от условий в газе (Т, Р, природа газа) от расстояния между электродами, их материала и формы. Ток разряда в этот момент достигает значения около 1 мкА и выше. Вольтамперная характеристика между областью насыщения и точкой пробоя описывает таунсендовский разряд.

Рассмотрим теорию разряда, предложенную Таунсендом, при низком давлении (порядка несколько миллиметров ртутного столба), когда между электродами укладывается много длин свободного пробега.

Будем считать, что электрическое поле однородное E = const, достигается применением плоских электродов, а расстояние между ними мало по сравнению с их размером; постоянное внешнее излучение (ионизатор) падает только на катод, где оно освобождает электроны. Эти электроны ускоряются полем, между столкновениями с нейтральными атомами газа и достаточно часто их энергия превышает энергию ионизации, т.е.

Таким образом, некоторые электроны на пути от катода к аноду ионизируют атомы, создавая положительные ионы и дополнительные электроны. Это дополнительные электроны также ускоряются, сталкиваются с атомами, вызывая их ионизацию и т.д. Это означает, что ток разряда увеличивается по сравнению с его значением при насыщении, так как число электронов, приходящих за 1с на анод, больше положительные ионы. Пусть через единицу поверхности, поставленную перпендикулярно электронному потоку, за единицу времени пролетает по направлению к аноду n электронов (n-плотность потока электронов).

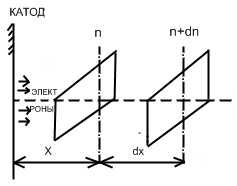
Увеличение плотности потока электронов dn на расстояние dx вследствие ионизации ударом будет dn = αndx,где α -коэффициент пропорциональности, называется коэффициентом объемной ионизации. Значение α равно числу дополнительных электронов, образуемых одним электроном при соударении с атомами газа на пути в 1см. Для однородного поля (E = const) коэффициент α можно считать постоянной величиной, не зависящей от х. Тогда, интегрируя, найдем закон нарастания электронной лавины: n = ce^αx, с − постоянная интегрирования. У катода: х = 0; n = n_k, у анода x = a, n = n_а и число электронов, попадающих за одну секунду на единицу площади анода будет n_a = n_ke^αα

Число дополнительных электронов, возникающих за 1 секунду в межэлектродном единичном объеме, будет равно:

n_a –n_k = n_ke ^αα – n_k = n_k (e^αα – 1)

Этим уравнением определяется также число положительных ионов, возникающих в процессе ударной ионизации. Все эти положительные ионы (числом n_k (e^αα −1)), ударяясь о катод, создают плотность потока вторичных электронов. Число вторичных электронов равно γn_k (e^αα−1), γ − коэффициент пропорциональности или вторичной эмиссии. Таким образом, у катода имеются электроны, выбитые из поверхности ионизатором, плотность потока которых обозначим через n₀, имеются электроны вторичной эмиссии, выбитые положительными ионами. Общее число электронов у катода для установившегося процесса будет:

n_k = n₀ + γn_k (e^αα −1)

или

.

А общее число электронов (вернее плотность потока электронов) у анода будет:

.

У анода нет положительных ионов (все ионы направляются электрическим полем на катод), поэтому весь разрядный ток у анода переносится только электронами, плотность тока у анода j_a = en_a, плотность тока в других точках разряда j=j_e+j_i, т.е. ток переносится и электронами, и ионами. Однако для разряда j = const, следовательно, j = j_a. Тогда имеем

= j₀

Полученное выражение показывает, что плотность тока в таунсендовском разряде (следовательно, и полный ток) зависит от коэффициента объемной ионизации α, коэффициента вторичной эмиссии γ и межэлектродного расстояния а. Однако в общем случае, когда электрическое поле переменное коэффициент α зависит от Е и от условий в газе. Состояние газа характеризуется давлением и температурой. Нагревание газа пренебрежимо мало, обычно считают, что Т = const. Для зависимости α от Е и р Таунсенд предложил следующую приближенную формулу:

,

где А и В − константы, зависящие от природы газа.

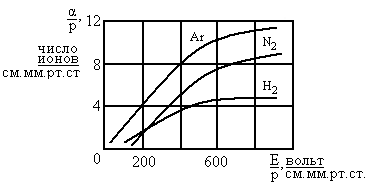
Типичные кривые зависимости α/p от E/p для различных газов приведены на рисунке. Величину γ, так же как α/p, представляют в виде функции от E/p, т.е. γ/p = можно получить графики этой зависимости (Хават,стр.49).

Таусендовский разряд находит практическое применение как средство регистрации внешнего излучения, т.е. в приборах, подобных фотоэлементу. Начальное значение тока i₀ или плотности тока определяется внешним излучением, например падающим светом. Отношение называется коэффициентом умножения. Разность потенциалов на электродах; очевидно, должна быть меньше напряжения пробоя.

Плотность потока электронов у катода для стационарного таунсендовского разряда определялась выражением n_k = n₀ + γn_k (e^αα – 1).

Теперь рассмотрим случай, когда ионизатора убирают, а это означает, что n₀ = 0 и γ (e^αα – 1) = 1. Для выполнения этого условия, т.е γ (e^αα – 1) = 1, необходимо, чтобы коэффициенты α и γ принимали соответствующие значения, а они зависят от напряженности поля в межэлектродном промежутке, т.е. Е должна принять определенное значение. С учетом U = , можно сделать вывод, что выражение γ (e^αα – 1) = 1 становится равным единице, называется направлением пробоя газа.

Общая теория самостоятельного разряда весьма сложна и не завершена до сих пор. Поэтому при изучении и применении самостоятельных разрядов пользуется законами и формулами, полученными опытным путем. Например: опытный закон Пашена гласит о том, что пробой газа происходит при постоянном для каждого газа отношении напряженности поля к давлению газа, т.е , т.е. постоянная зависит от природы и состояния газа.

Этот закон можно пояснить следующим образом, если принять, что начало самостоятельной проводимости газа совпадает с началом ионизации ударом:

= eU = eλE_п = e

т.е. при постоянной температуре . Для однородного поля U_п= E_пa и закон Пашена или U_п = (pa)const. В общем случае закон Пашена можно записать в виде U_п = f(pa), теоретическое выражение функций f не найдено, существуют приближенные формулы, согласующиеся с экспериментом в одном ватном отношении: кривая зависимости U_п от произведения (ра) для любых комбинации газов и материалов электродов имеет единственный минимум. Некоторые экспериментальные кривые показаны на рис.

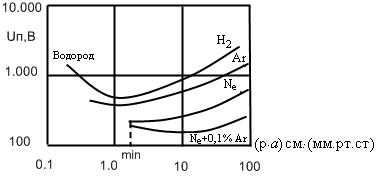
Для некоторых газов небольшая добавка другого газа сильно влияет на ход кривой U_п = f(pa). Например, небольшое количество аргона заметно понижает потенциал пробоя неона. Электроды с низкой работой выхода, например, содержащие щелочные металлы, имеют высокие значения γ и потому уменьшают напряжение пробоя газа.