Билет № 14

1. Начертить прямоугольную призму, основанием которой является треугольник. Построить сечение, проходящее через сторону нижнего основания и противолежащую вершину верхнего. Как вычислить его площадь? В каком отношении оно делит объем призмы?

2. Определить экстремумы функции y=2x²-x⁴/

3. Скорость тела, движущегося по закону V(t)=2t²+1 (м/с² ). Какой путь пройдет тело с первой по третью секунды?

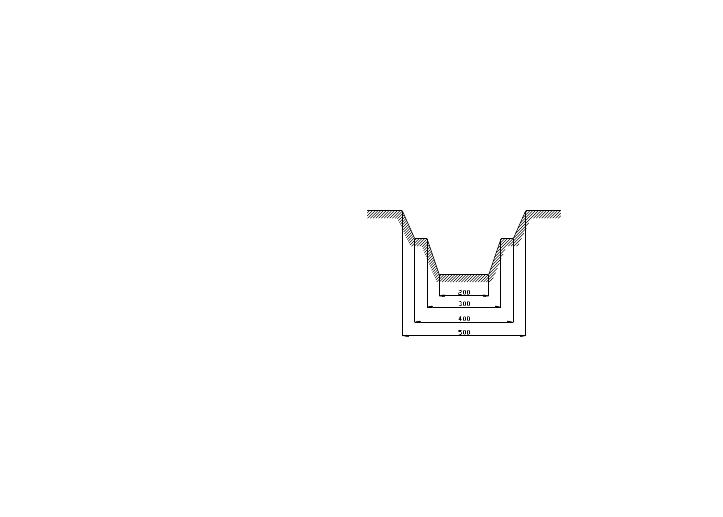
4. Поперечное сечение траншеи показано на чертеже. Размеры даны в см. Определить объем земляных работ для траншеи длинной 40м.Каким многогранником является данная траншея?

Билет № 15

1. Начертить цилиндр и его развертку. Показать на ней все соответствующие элементы цилиндра.

2. Определить наибольшее и наименьшее значения функции y=2x³-15x²+24x-7 на отрезке [0;4].

3. Найти площадь фигуры, ограниченной графиками функций y=x²-4x+8; x=1; x=3;y=0.

4. Площадь прямоугольного участка земли 48м². Какую длину должны иметь его стороны, чтобы периметр был наименьшим?

Билет № 16

1. В виде какой геометрической фигуры можно представить траншею с поперечным сечением в виде трапеции? Ответ обоснуйте. Как определить объем такого многогранника?

2. В чем заключается геометрический смысл производной? Для функцииy=x²-2x+3 составить уравнение касательной в точке x₀=2.

3. Закон изменения скорости от времени для прямолинейно движущейся точки задан уравнением V(t)=t³+42.Какой путь пройдет точка за первые 3 секунды.

4. Кусок проволоки длиной 36м сгибают так, чтобы образовался прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей?

Билет № 17

1. Начертите правильную четырехугольную пирамиду и её развертку. Показать на ней все соответствующие элементы пирамиды.

2. Вычислить тангенс угла наклона касательной к графику функции y=-x²+4x в точке x₀=1.

3. Вычислить площадь фигуры, ограниченной линиями: y=x²-2x, y=0.

4. Котлован, вырытый для фундамента и подвала, представляет собой в верхней части прямоугольник размерами 120×80м, в нижней части 81×54м. Высота котлована 6м. Определите объем земляных работ. Какая геометрическая фигура определяет форму этого земляного сооружения

Билет № 18

1. Начертите прямоугольный параллелепипед и его развёртку. Покажите на развертке соответствующие элементы многогранника.

2. Чем характеризуется производная монотонно убывающей функции. Приведите пример. Исследуйте на монотонность функцию y=4 .

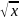3. Найдите совокупность первообразных функции y= 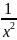+cosx, и ту из них, график которой проходит через точку М ( ;1).

4. В правильной 4-х угольной призме диагональ равна 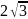. При какой высоте призмы объём её будет наибольшим?

Билет № 19

1. Какой геометрической фигурой является диагональное сечение прямоугольного параллелепипеда, четырёхугольной пирамиды, четырёхугольной усеченной пирамиды. Как оно вычисляется в этих многогранниках.

2. Составьте уравнение касательной для точки максимума функции .

3. Вычислите площадь криволинейной трапеции, ограниченной линиями , , , .

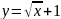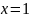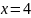4. Периметр осевого сечения цилиндра равен 36 см. При каком радиусе основания цилиндр будет иметь наибольший объём? Вычислить его.