Тема: механика

1. Кинематика поступательного движения. Скорость и ускорение материальной точки. Составляющие ускорения. Кинематическое уравнение

• Кинематика поступательного движения

Поступательное движение - это движение, при котором любая прямая, жестко связанная с движущемся телом, остается параллельной своему первоначальному положению. Так движется, например кабина лифта или кабина колеса обозрения. При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела), так же при поступательном движение движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и параллельны между собой, также равны и параллельны между собой ускорения всех точек.

Следовательно, при поступательном движении тела все его точки описывают одинаковые траектории и в любой момент времени имеют равные по модулю и параллельно направленные скорости и ускорения.

Скорость - векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

Средняя скорость движения: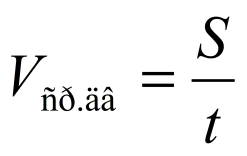

Средняя скорость перемещения: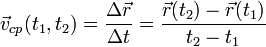

Мгновенная скорость – производная от радиус-вектора по времени.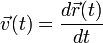

Характеризует быстроту перемещения материальной точки. Мгновенная скорость всегда направлена по касательной к траектории.

Ускорение - векторная величина, характеризующая быстроту изменения вектора скорости тела во времени. Ускорение изменяет не только скорость тела, но и направление движения.

Вектор ускорения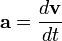

При движении точки по окружности можно разложить на два слагаемых (компоненты):

Составляющие ускорения Тангенциальное ускорение — направлено по касательной к траектории Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.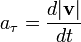

Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

Кинематическое уравнение Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени: x=x(t); y=y(t); z=z(t)

либо зависимость от времени радиус-вектора этой точки Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.

2)Движение по окружности. Угловые скорость и ускорение. Период и частота вращения. Связь между линейными и угловыми величинами.

Движение по окружности-явл частным случаем криволинейного движения

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:

Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно — при замедленном).

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени: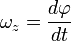

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Период и частота вращения

Число оборотов в единицу времени есть величина, обратная периоду, — циклическая частота вращения

Время, за которое тело совершает один оборот, т.е. поворачивается на угол , называется периодом обращения. Так как промежутку времени соответствует угол поворота , то

откуда Число оборотов в единицу времени, очевидно, равно:

отсюда следует, что угловая скорость

Связь между линейными и угловыми величинами выражается следующими ф-лами: S=R*φ; V=ω*R; a_t=R*ε; a_n= ω²*R где φ-угол поворота; ω-угл скорость; R-расстояние; ε-угл ускорение.