МИНИСТЕРСТВО ОБРАОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ

ТОРГОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ»

Кафедра информационных технологий и математического моделирования

Отчет

По Лабораторной работе №4

Вариант-3

Выполнили: Проверил:

студентка 3 курса профессор, д.т.н.

группы ЭУ-09-2Д Шишов В.В.

Иваненкова Кристина Владимировна

Красноярск 2011

Лабораторная работа № 4

На основе таблицы данных (см. Приложение) для соответствующего варианта :

1. Построить уравнение линейной множественной регрессии в стандартизированном масштабе.

2. Оценить информативность факторов на основе уравнения линейной регрессии в стандартизированном масштабе.

3. Вычислить частные коэффициенты корреляции.

4. Оценить их значимость при уровнях значимости 0,05 и 0,01.

5. Оценить информативность факторов на основе частных коэффициентов корреляции.

6. Проверить гипотезу о гомоскедастичности ряда остатков с уровнем значимости α = 0,05.

Решение

1. Для построения линейной множественной регрессии в стандартизированном масштабе, необходимо перейти к новым зависимой переменной t_y и независимым переменным t_x1, t_x2, t_x3, t_x4, t_x5, t_x6, стандартизировав исходные переменные по формулам:

Для этого добавили две дополнительные строки к исходной таблице. В одной из которых посчитали средние значения переменных. И эти значения нашли по каждой переменной при помощи функции СРЗНАЧ( ). По другой строке рассчитали среднеквадратическое отклонение всех переменных при помощи функции СТАНДОТКЛОН ( ).

После этого подставив полученные значения в вышеприведенные формулы получили следующую таблицу стандартизированных переменных:

№	tx1	tx2	tx3	tx4	tx5	tx6	y
п/п
7	-1,47483	-1,25035	-1,18197	-1,72324	2,20485	0,34043	-1,42653
8	1,16819	0,92632	1,34315	-0,04787	0,81718	-0,73979	0,82057
9	0,51108	0,46859	0,31409	0,67015	-0,10793	0,43864	0,62490
10	1,06644	1,04651	0,86375	-0,28721	-0,57049	0,83144	0,88369
11	1,06832	1,48118	0,79349	-0,28721	0,81718	-1,13260	1,23086
12	-0,12436	-0,24763	0,11985	1,38817	-0,33921	0,73324	0,10731
13	-1,40606	-1,27340	-1,50433	-2,20192	-2,18943	1,12605	-1,48965
14	0,52710	0,30065	0,67364	1,14883	1,27974	-1,82001	0,68171
15	-0,75979	-0,62139	-0,85135	-0,04787	-0,57049	1,02785	-0,66908
16	1,04053	0,93620	0,84309	-0,28721	-0,33921	0,04583	0,74483
17	-1,07209	-1,02313	-1,12412	-0,04787	-0,10793	-0,83799	-1,04781
18	-0,85730	-0,85519	-0,92987	-0,28721	-0,10793	1,42066	-0,92156
19	0,35422	-0,01218	0,37608	1,14883	0,12335	0,34043	0,29036
20	0,97412	1,33629	1,32662	-0,04787	-0,57049	-1,42720	1,28135
21	-1,01557	-1,21248	-1,06212	0,90949	-0,33921	-0,34698	-1,11093
ср.знач.	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
ср.кв.откл.	1,0	1,0	1,0	1,0	1,0	1,0	1,0

Для проверки корректности стандартизации рассчитали все средние и среднеквадратические отклонения для новых переменных. Все средние равны нулю, а среднеквадратические отклонения единице.

Для нахождения некоррелированных новых независимых переменных воспользуемся методом, описанным в лабораторной работе 3 на основе матрицы корреляции. Используя команду в «Анализе данных» - «Корреляция» получили матрицу, которая выглядит следующим образом:

	Столбец 1	Столбец 2	Столбец 3	Столбец 4	Столбец 5	Столбец 6	Столбец 7
Столбец 1	1
Столбец 2	0,974919	1
Столбец 3	0,980542	0,954039	1
Столбец 4	0,372545	0,241334	0,391556	1
Столбец 5	0,130621	0,121915	0,199971	0,132849	1
Столбец 6	-0,43352	-0,45139	-0,49165	-0,28641	-0,4311	1
Столбец 7	0,982555	0,977766	0,975637	0,416961	0,148592	-0,4819	1

Можно сделать вывод, что матрица у нас получилась точно такая же, как и в лабораторной работе №3. А следовательно, применив алгоритм исключения переменных, у нас останутся так же независимые переменные x₁ и x₆, только в стандартизированном масштабе, т.е. t_x1 и t_x6. Регрессионное уравнение будет выглядеть следующим образом:

у = а₀ + а₁х₁ + а₂х₆

Используя «Сервис» – «Анализ данных» – «Регрессия», получили таблицу «Вывод итогов». При этом преобразовали исходную таблицу следующим образом:

№ п/п	tx1	tx6	y
7	-1,4748	0,3404	-1,4265
8	1,1682	-0,7398	0,82057
9	0,5111	0,4386	0,6249
10	1,0664	0,8314	0,88369
11	1,0683	-1,1326	1,23086
12	-0,1244	0,7332	0,10731
13	-1,4061	1,1261	-1,4897
14	0,5271	-1,8200	0,68171
15	-0,7598	1,0278	-0,6691
16	1,0405	0,0458	0,74483
17	-1,0721	-0,8380	-1,0478
18	-0,8573	1,4207	-0,9216
19	0,3542	0,3404	0,29036
20	0,9741	-1,4272	1,28135
21	-1,0156	-0,3470	-1,1109

В качестве входного диапазона значения у указывается значения чистой прибыли, а в качестве входного интервала для х указывается диапазон значений, содержащий t_х1 (суммарные активы) и t_х6 (износ основных производственных фондов). Получилось следующее множественное регрессионное уравнение, содержащее две независимых переменных:

y = -1,03692E-18 + 0,952692045tx1 -0,068885345tx6

2. Коэффициент регрессии при t_x1, равный 0,952692045, по модулю больше, чем коэффициент при t_x6, равный 0,068885345. Значит можно сделать вывод, что наиболее информативной и больше оказывающей влияние на зависимую переменную t_y является независимая переменная t_x1.

3. Рассчитали частные коэффициенты корреляции между стандартизированными y и хi по формуле:

Где:

- R²_{yx1x2..xi..xp} - общий коэффициент детерминации, который находится на странице вывода итогов в таблице Регрессионная статистика: R-множественный, в нашем случае он равен 0,984514199.

- R²_{yx1x2…xi-1xi+1..xp} – коэффициент детерминации, полученный при исключении стандартизированной переменной xi из регрессионного уравнения. В нашем примере будет р=2. Следовательно у нас получится два частных коэффициента:

Сначала нашли коэффициент детерминации исключив из регрессионного уравнения переменную t_x1. Т.е. при проведении процедуры регрессии в качестве входного интервала Y указали все значения переменной t_y, а в качестве входного интервала X указали все значения переменной t_x6. И на странице выводов итогов нашли в таблице регрессионная статистика значение R²_yx6= 0,481897.

Затем нашли коэффициент детерминации исключив из регрессионного уравнения переменную t_x6. Т.е. при проведении процедуры регрессии в качестве входного интервала Y указали все значения переменной t_y, а в качестве входного интервала X указали все значения переменной t_x1. И на странице выводов итогов нашли в таблице регрессионная статистика значение R²_yx1= 0,982555.

Подставив полученные значения в формулу, приведенную выше, получили следующие результаты: r_yx1= 0,335103319, r_yx6 = 0,984941918.

4. Проверили значимость частных коэффициентов применив критерий Стьюдента. Для этого нашли F расчетное по формуле:

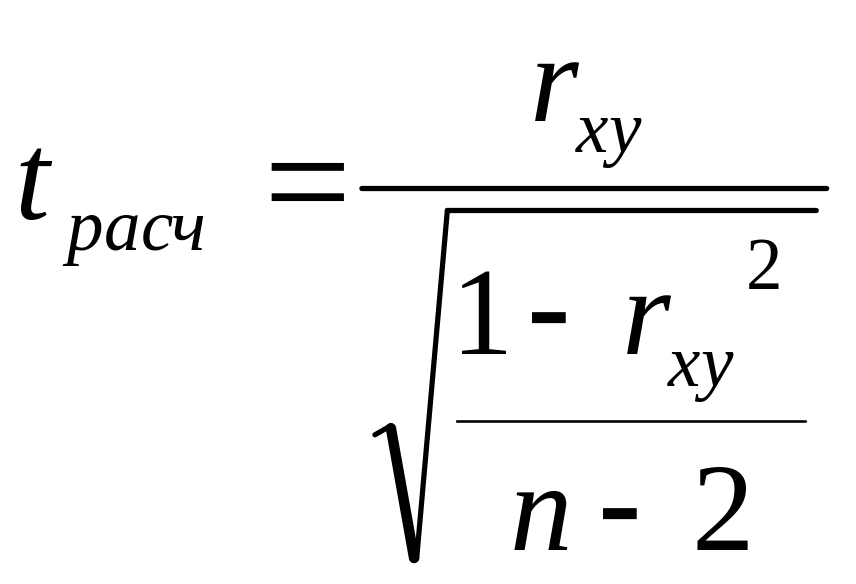, где r_xy-коэффициент регрессии,

n-количество наблюдений, и равно 15.

И так для r_yx1 Fрасч1 = 1,282377, а для r_yx6 Fрасч6 = 20,54109.

А Fкрит с уровнем значимости 0,05 = 2,1604. Сравнивая полученные Fрасч и Fкрит можно сделать следующие выводы:

Fрасч1 < Fкрит (1,282377 < 2,1604), следовательно можно утверждать, что с вероятностью р=0,95 коэффициенты корреляции между t_x1 и t_y не коррелированны.

Fрасч6 > Fкрит (20,54109 > 2,1604), следовательно можно утверждать, что с вероятностью р=0,95 коэффициенты корреляции между t_x6 и t_y положительно коррелированны.

Fкрит c уровнем значимости 0,01 = 3,0123. Так же сравнив Fкрит c Fрасч сделали следующие выводы:

Fрасч1 < Fкрит (1,282377 < 3,0123), следовательно можно утверждать, что с вероятностью р=0,99 коэффициенты корреляции между t_x1 и t_y не коррелированны.

Fрасч6 > Fкрит (20,54109 > 3,0123), следовательно можно утверждать, что с вероятностью р=0,99 коэффициенты корреляции между t_x6 и t_y положительно коррелированны.

5. Частный коэффициент регрессии r_yx6, равный 0,984941918, больше, чем частный коэффициент r_yx1, равный 0,335103319. Значит можно сделать вывод, что наиболее информативной и больше оказывающей влияние на зависимую переменную t_y является частный коэффициент корреляции r_yx6.

6. Проверили гипотезу о гомоскедастичности ряда остатков у уровнем значимости при помощи метода Гольдфельда-Квандта.

Сначала применили метод Гольдфельда-Квандта для независимой переменной tx1.

Упорядочили значения в таблице в порядке возрастания переменной t_x1. Для этого использовали процедуру сортировки, выделив весь диапазон значений таблицы.

№ п/п	tx1	tx6	y
7	-1,4748	0,3404	-1,426532
13	-1,4061	1,1261	-1,489653
17	-1,0721	-0,8380	-1,047807
21	-1,0156	-0,3470	-1,110927
18	-0,8573	1,4207	-0,921565
15	-0,7598	1,0278	-0,669081
12	-0,1244	0,7332	0,1073055
19	0,3542	0,3404	0,290356
9	0,5111	0,4386	0,6248967
14	0,5271	-1,8200	0,6817055
20	0,9741	-1,4272	1,2813538
16	1,0405	0,0458	0,7448264
10	1,0664	0,8314	0,8836923
11	1,0683	-1,1326	1,2308571
8	1,1682	-0,7398	0,8205714