1. Все частные суммы ряда ограничены, то есть ;

2.  .

Тогда ряд сходится.

Доказательство.

1. Согласно первому ограничению мы имеем

Пусть

.

Тогда .

2.   .

3. Считая, что , , а также, что и используем преобразование Абеля. Получаем (вначале особых пояснений не требуется):

(делаем преобразование Абеля)

И тут наступает самый тонкий момент вывода. Вспомним, что, согласно ограничению 2, монотонно убывают. Поэтому все разности вида отрицательны, то есть . В силу этого

,

и, продолжая прерванный вывод, получим:

.

Но  сколь угодно мало. Поэтому, со ссылкой на признак сходимости БольцаноКоши, можно утверждать, что ряд сходится. 

Следствие. Если , то сходятся ряды (при ) и (при любых х).

Доказательство.

Пусть . Начнем с известной со школы формулы

.

Имеем

k = 1: ;

k = 2: ;

k = 3: ;

……………..

k = n: .

Складывая все эти равенства, получим:

.

Теперь мы имеем очень интересную формулу

.

Но тогда

,

если , то есть, если . По признаку Дирихле, при ряд сходится.

Для ряда все выкладки совершенно аналогичны, надо только начинать с формулы

.

Условие можно убрать, так как при и сумма ряда просто равна нулю.

Признак Абеля. Если ряд сходится (не обязательно абсолютно!), а последовательность чисел монотонна и ограничена, то ряд сходится.

Доказательство.

1. Ряд сходится  по признаку БольцаноКоши

.

2. Последовательность чисел ограничена  .

3. Дальнейшие выкладки сначала полностью повторяют признак БольцаноКоши

(делаем преобразование Абеля)

С этого момента начинаются отличия. Если раньше действовала оценка , то теперь будет оценка :

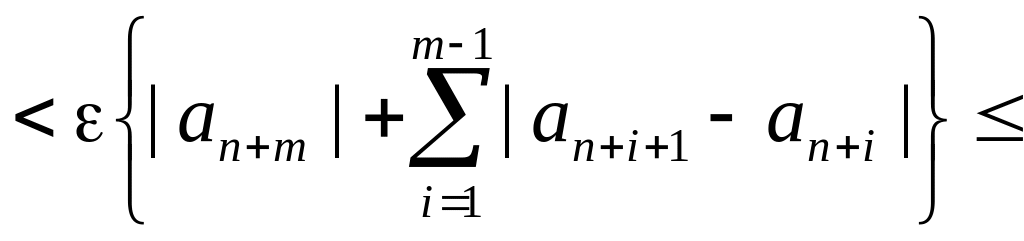
В этом месте  самый тонкий момент. Согласно ограничению, последовательность чисел монотонна  все разности одного знака, или все положительные, или все отрицательные. Поэтому можно записать

.

Поэтому, продолжая доказательство, можно записать:

.

Заключительная фраза та же самая:  сколь угодно мало. Поэтому, со ссылкой на признак сходимости БольцаноКоши, можно утверждать, что ряд сходится. 

9.9 Сочетательное свойство сходящихся рядов

Рассмотрим два ряда

который будем называть рядом (А), и ряд

,

который будем называть рядом ( ).

Теорема. Если ряд (А) сходится, то ряд ( ) тоже сходится и имеет ту же сумму.

Доказательство.

Пусть есть частная сумма ряда (А), то есть . Рассмотрим теперь частные суммы ряда ( ). Имеем

; ; ; … .

Но тогда, если , то и , потому, что последовательность есть подпоследовательность последовательности . 

Замечания.

1. Это свойство нельзя применять наоборот, то есть из сходимости ряда ( ) не следует сходимость ряда (А). Другими словами, в сходящемся ряду собирать слагаемые в группы и заключать эти группы в скобки можно, а вот раскрывать скобки, вообще говоря, нельзя, точнее, надо делать это очень осторожно. Это можно делать лишь тогда, когда ряд, получающийся после раскрытия скобок, является сходящимся рядом, а это надо доказывать.

Пример. Ряд

сходится и сумма его равна нулю, а вот ряд, полученный после раскрытия скобок,

расходится, так как его общий член не стремится к нулю.

2. Это свойство неверно для расходящихся рядов, то есть в расходящемся ряду собирать слагаемые в группы и заключать эти группы в скобки нельзя.

Пример. Ряд

расходится, но ряды

,

сходятся, и имеют разные суммы.