8.11 Обобщенная формула интегрирования по частям
Пусть даны две функции и . Напомним формулу интегрирования несобственных интегралов по частям:
.
В последующих выкладках эта формула каждый раз применяется к последнему слагаемому.
.
Коротко эта формула может быть записана так:
Эта формула носит имя обобщенной формулы интегрирования по частям.
Для определенных интегралов эта формула принимает вид
.
8.12 Остаточный член ряда Тейлора в интегральной форме
Запишем предыдущую формулу в виде
.
Возьмем
и
.
Тогда легко получить, что
,
.
В частности,
и
.
Подстановка в обобщенную формулу интегрирования по частям дает
.
Но
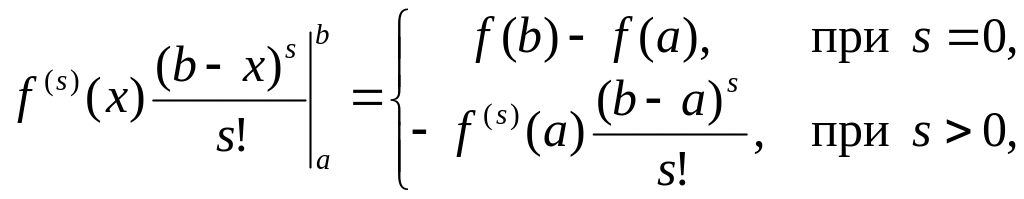
и предыдущая
формула, после сокращения сомножителя
,
примет вид
.
Записывая ее в виде
мы узнаём в ней формулу Тейлора с остаточным членом в виде
.
Это выражение и носит название остаточного члена ряда Тейлора в интегральной форме. Применение к интегралу первой теоремы о среднем дает остаточный член в форме Лагранжа.