8.9 Интегралы Фруллани

Пусть

1. функция определена и непрерывна при ;

2. существует конечный ;

3.  .

Рассмотрим следующий интеграл:

.

Имеем

В первом интеграле сделаем замену переменных , во втором  : получаем

И теперь  самое интересное. Посмотрите на области интегрирования первого и второго интегралов:

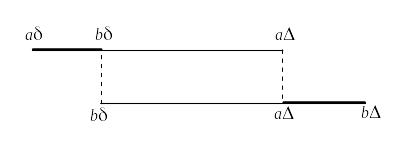
У них есть общая часть  отрезок . Подынтегральные функции одинаковы, интегралы вычитаются  следовательно, интегралы по этой области сокращаются. Остается

А теперь срабатывает первая теорема о среднем

,

где , .

А теперь сделаем предельный переход при , . Тогда , и мы получаем

.

Интеграл называется интегралом Фруллани. Полученная формула позволяет легко вычислять их.

8.10 Интегральные неравенства

Неравенство Гёльдера.

Выведем одно из важнейших неравенств математического анализа  неравенство Гёльдера.

Пусть p и q  вещественные числа, такие, что

1.  , :

2. (самое главное) .

Прежде, чем выводить само неравенство, выведем некоторые промежуточные формулы, чтобы потом не отвлекаться. Имеем

; ; ; .

А теперь  вперед!

Неравенство Гёльдера в простейшей форме

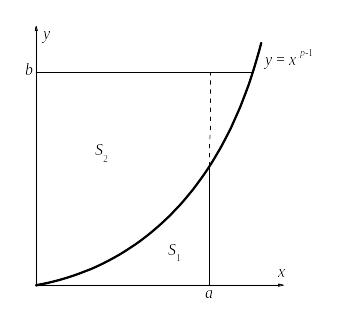
Рассмотрим график функции (см. рисунок):

Сосчитаем площади областей, указанных на рисунке. Имеем . Из уравнения , следует, что (см. вспомогательные формулы) и поэтому . Но, как видно из рисунка, , и поэтому .

При выводе этой формулы неявно предполагалось, что и . Для произвольных а и b это неравенство можно записать в виде

.

Это и есть знаменитое неравенство Гёльдера.

Заметим, что могут быть и другие варианты поведения графика функции и другое соотношение между а и b, но результат всюду будет тот же. Попробуйте сами рассмотреть другие варианты. Кстати, для каких значений параметра р график функции выглядит так, как это изображено на рисунке?

Неравенство Гёльдера для сумм

Пусть даны два набора чисел  и . Возьмем в неравенстве Гёльдера

и .

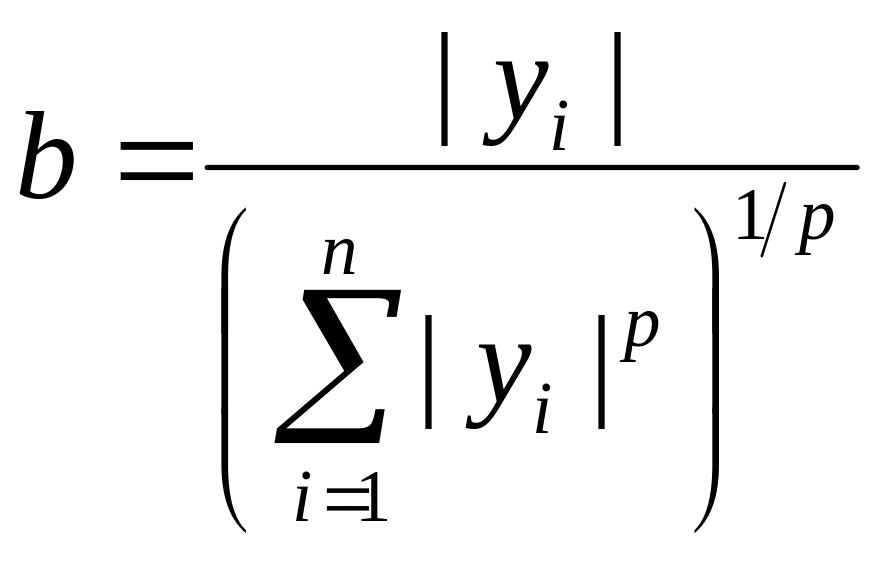Тогда неравенство Гёльдера даёт

.

Складывая все эти неравенства, получим

,

откуда получаем

,

что и представляет собой неравенство Гёльдера для сумм.

В случае р = 2 также и q = 2 неравенство Гёльдера принимает вид

.

Неравенство Гёльдера для интегралов

Пусть и  две функции, интегрируемые на . Возьмем в неравенстве Гёльдера

и .

Тогда неравенство Гёльдера даёт

.

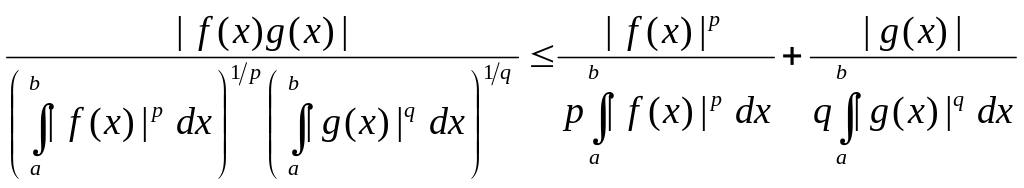Интегрируя это неравенство, получим

откуда получаем

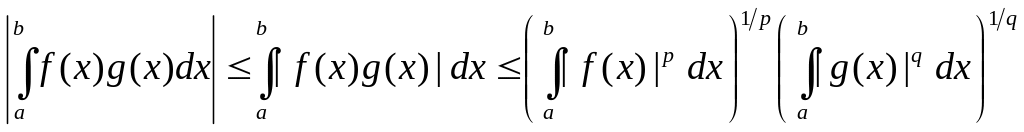
что и представляет собой неравенство Гёльдера для интегралов.

В случае р = 2 также и q = 2 и неравенство Гёльдера принимает вид

.

Это неравенство называется неравенством БуняковскогоКошиШварца.

Неравенство Минковского

Неравенство Минковского для сумм.

Пусть даны два набора чисел  и . Тогда имеем

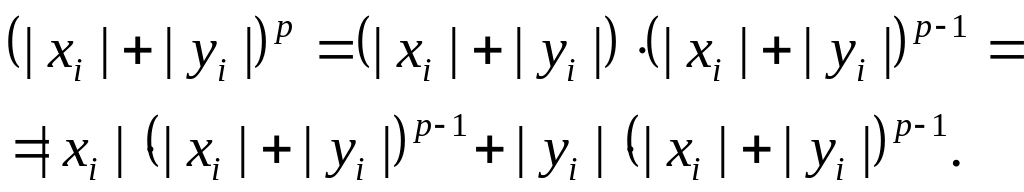
Просуммируем эти выражения и к каждой сумме в правой части применим неравенство Гёльдера. Тогда получим

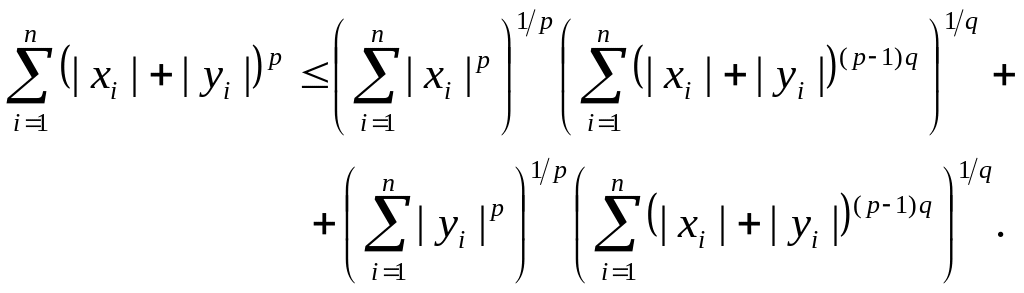
Но (см. вспомогательные формулы) , и мы получаем

Деля обе части неравенства на 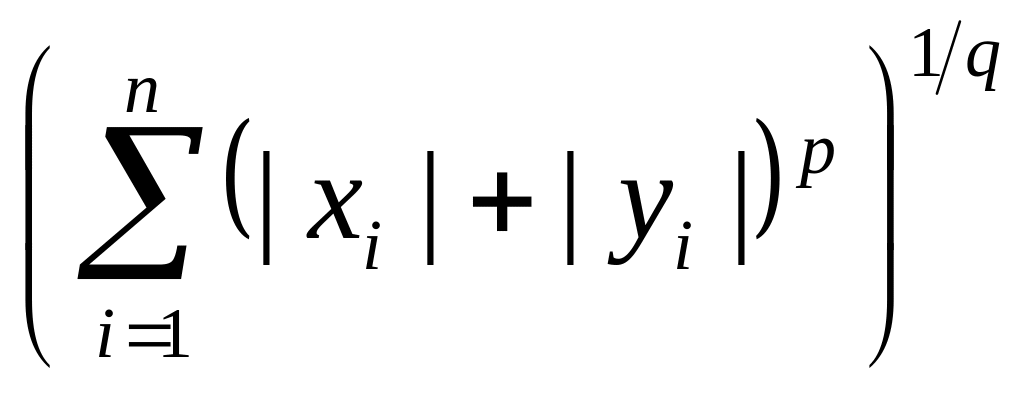и учитывая, что , получим неравенство

которое и носит название неравенства Минковского. В частном случае р = 2 оно принимает вид

,

которое Вы знаете еще со школы (длина стороны треугольника меньше суммы длин двух других сторон).

Неравенство Минковского для интегралов.

Пусть и  две функции, интегрируемые на . Имеем, аналогично предыдущему,

.

Интегрируя и применяя к каждому интегралу в правой части неравенство Гёльдера для интегралов, получаем

Принимая снова во внимание, что будем иметь

Деля на 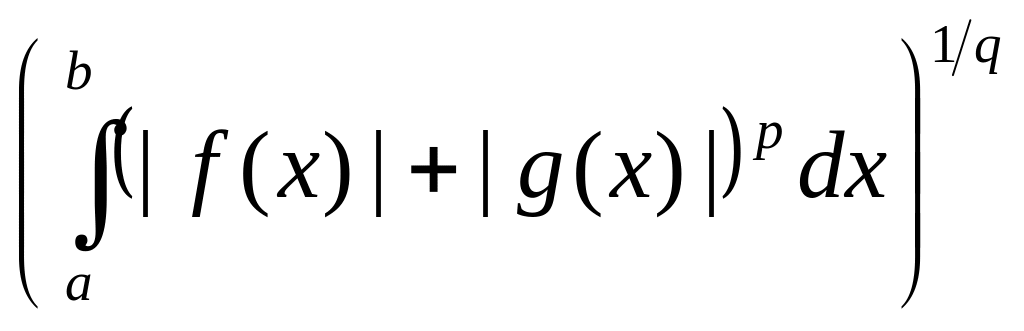и снова учитывая, что учитывая, что , получим неравенство

,

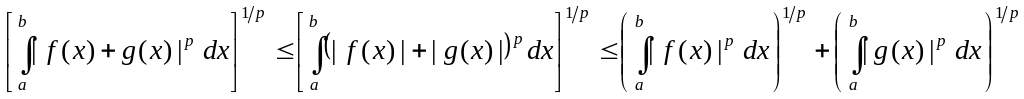которое также носит название неравенства Минковского. В частном случае р = 2 оно принимает вид

.

Неравенство Иенсена

Это неравенство мы выведем не очень строго.

Пусть

1.  есть выпуклая на функция:

2.  и ;

3.  непрерывная функция.

Вспомним теперь неравенство Иенсена

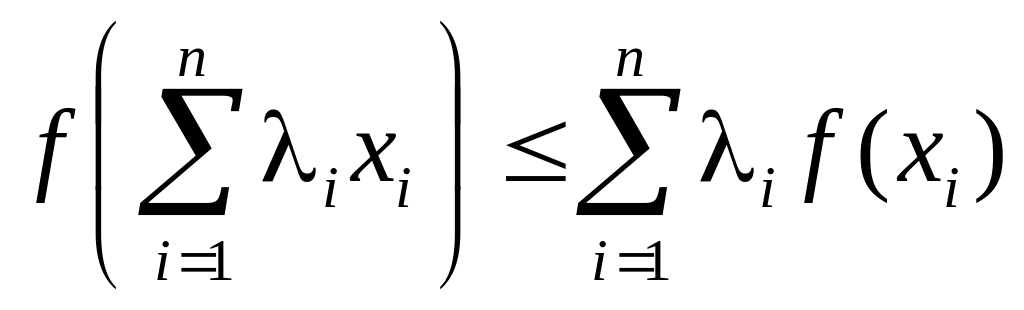
и сделаем в нем следующие замены:

, а заменим на . Тогда неравенство Иенсена примет вид

.

Сделаем теперь в этом неравенстве предельный переход . Тогда суммы перейдут в интегралы, и мы получим неравенство

.

Это неравенство и называется неравенством Иенсена в интегральной форме.