8.5 Несобственные интегралы второго рода
Итак, в несобственных интегралах первого рода снимается ограничение конечности промежутка интегрирования. В несобственных интегралах второго рода снимается ограничение ограниченности подынтегральной функции.
Будем называть с
особой точкой
функции
если
.
А теперь рассмотрим определение несобственных интегралов второго рода. Пусть речь идет об интеграле , но b является особой точкой функции . Как поступить в этом случае?
Основная идея
заключается в том, чтобы немного отступить
от особой точки. Поэтому рассмотрим
отрезок
,
где
.
Тогда на этом отрезке особых точек уже
не будет. Будем считать, что для этих
значений
существует интеграл
.
Тогда
естественно определить так:
,
который и называется
несобственным интегралом второго рода.
Если этот предел существует и конечен,
то говорят, что интеграл
сходится
(или: интеграл
существует);
если этот предел равен бесконечности
или вообще не существует, то говорят,
что интеграл
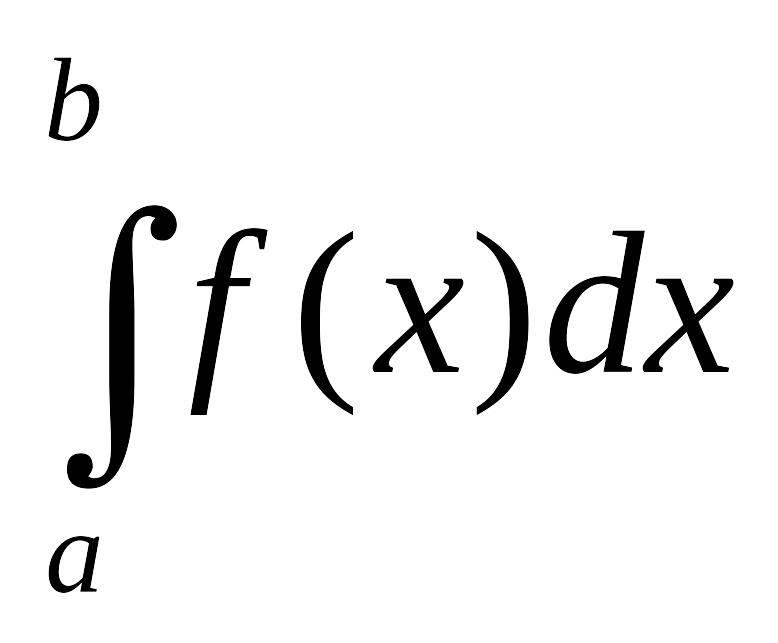расходится
(или: интеграл
не существует).
Аналогично, если особой точкой является левый конец промежутка интегрирования, то определяется так:
.
Наконец, если
особая точка с
лежит внутри промежутка интегрирования,
то есть
,
то
определяется так:
.
Если
есть первообразная функции
,
то в этом случае
.
Простейшие свойства несобственных интегралов второго рода полностью аналогичны соответствующим свойствам несобственных интегралов первого рода. Доказывать их мы не будем.
8.6 Сходимость несобственных интегралов второго рода от неотрицательных функций
Пусть функции
и
неотрицательны (то есть
и
) и точка b
является особой точкой
для обеих из них. Приводимые ниже теоремы
полностью аналогичны соответствующим
теоремам для несобственных интегралов
первого рода.
Теорема 1. Для сходимости необходимо и достаточно, чтобы
.
Доказательство.
Рассмотрим функцию
.
Если ,
то область интегрирования увеличивается,
а так как
,
то и
.
Поэтому, для существования конечного
,
согласно теоремы о монотонно возрастающей
функции, необходимо и достаточно, чтобы
она была ограниченной сверху, то есть
должно быть выполнено условие
,
что и требовалось доказать.
Теорема
2. Пусть
.
Тогда
А) из сходимости
следует
сходимость
;
Б) из расходимости
следует
расходимость
.
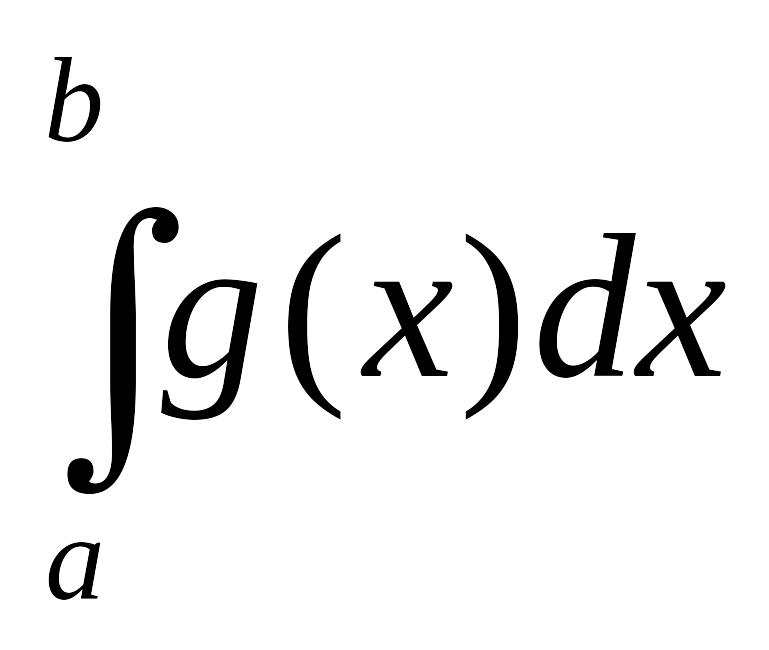Доказательство.
А) Пусть
сходится. Тогда, согласно теореме 1,
.
Но и поэтому
,
и, согласно теореме 1, сходится.
Б) Пусть
расходится. Так как
,
то это означает, что
.
Но, так как
,
то
,
и поэтому
,
что и означает,
что
,
то есть
расходится.
Теорема
3. Пусть
,
.
Тогда интегралы
и
сходятся или
расходятся одновременно.
Доказательство.
1. В формулировке теоремы сказано, что . Согласно определению предела это значит, что
.
(*)
2. Пусть сходится. В (*) рассмотрим вторую половину неравенства, которую запишем в виде . Тогда имеем следующую цепочку следований (сообразите сами, где идет ссылка на свойства несобственных интегралов и где на теорему 2):
сходится
сходится
сходится
сходится
сходится.
3. Пусть теперь сходится. Возьмем настолько малым, чтобы было . Тогда из левого неравенства в (*) следует, что и мы имеем следующую цепочку следований (и снова сообразите сами, где идет ссылка на свойства несобственных интегралов и где на теорему 2):
сходится
сходится
сходится
сходится
сходится.
Теперь мы имеем возможность доказать признак сходимости, который часто применяется при решении задач (доказательство проводится для случая, когда особая точка точка b.
Практический признак сходимости.
Пусть b
особая точка и
,
.
Тогда
сходится при
и расходится при
.
(Заметим снова, что вопрос о том, как же находить , остается на данном этапе открытым).
Доказательство.
Возьмем функцию
в виде
.
Тогда условие теоремы 3 примет вид
,
и
сходится
или расходится одновременно с интегралом
.
Рассмотрим
поэтому вопрос о сходимости этого
интеграла.
1. Пусть . Тогда
.
.
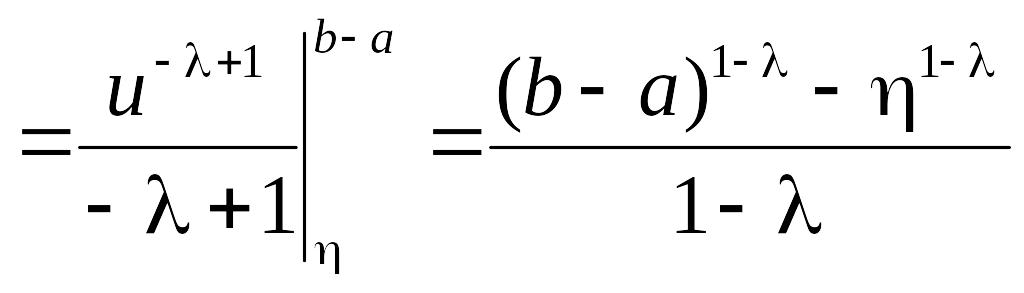Будут два варианта:
а)
.
В этом случае
,
поэтому
и
,
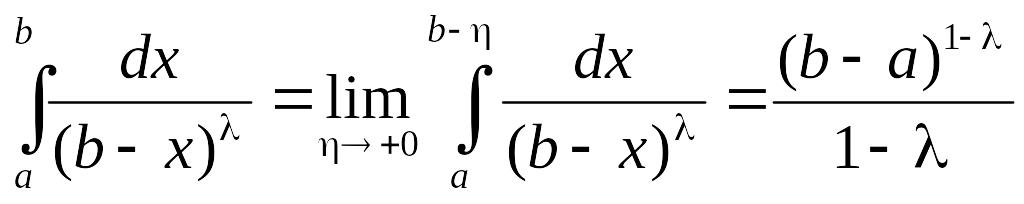так что сходится.
б)
.
В этом случае
,
поэтому
и
,
так что расходится.
2. . Тогда
,
так что
расходится.
Таким образом,
сходится
при
и расходится при
.
По теореме 2
также сходится при
и расходится при
.
Все упирается в нахождение величины . Как это делать будет разобрано на практике.