Глава 8. Несобственные интегралы
В предыдущей главе при построении теории определенного интеграла явно или неявно предполагались следующие ограничения:
1. отрезок
имеет конечную длину;
2. подынтегральная
функция
ограничена.
Определенные интегралы, построенные при этих ограничениях, называются «интегралами в собственном смысле», или, короче, «собственными интегралами».
Сейчас мы будем отказываться от этих ограничений, и построенные интегралы называются «интегралами в несобственном смысле», или просто «несобственными интегралами».
8.1 Несобственные интегралы первого рода
Пусть
1. функция
определена на отрезке
;
2. 
существует
.
Произведем теперь
предельный переход
.
Тогда
называется несобственным
интегралом первого рода и
обозначается символом
:
=
.
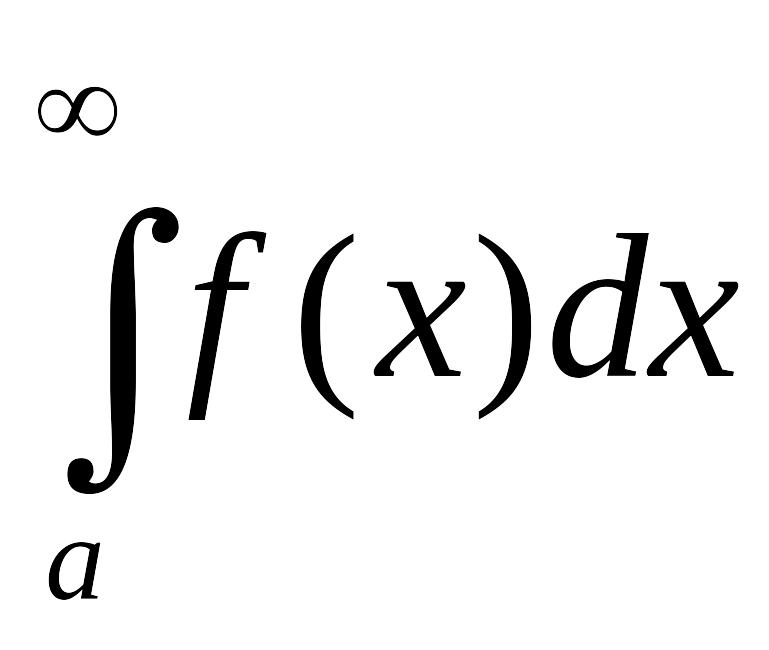Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится (или: существует). Если этот предел равен бесконечности или вообще не существует, то говорят, что несобственный интеграл расходится (или: не существует).
Совершенно аналогично определяются и следующие несобственные интегралы первого рода:
,
(а
любое).
8.2. Простейшие свойства несобственных интегралов первого рода
Рассмотрим простейшие свойства несобственных интегралов первого рода.
1. Если сходится
,
то
сходится и
.
Наоборот, если
сходится и существует
,
то сходится и
.
При этом верно соотношение
.
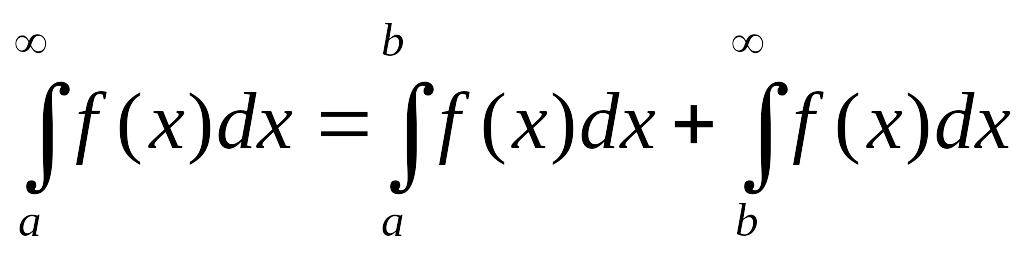Доказательство.
Пусть
.
Тогда имеем
.
Сделаем предельный переход А:
.
Так как предел слева существует, то существует и предел справа и сходится и соотношение принимает вид
.
Подумайте сами, что надо изменить в предыдущей фразе, чтобы доказать обратное утверждение.
2. Если
сходится, то
Доказательство.
Согласно предыдущему пункту
Отсюда
.
Делая предельный переход А, получаем
3. Если сходятся
и
,
то сходится также и
и верно соотношение
= ± .
Доказательство. Имеем
.
Делая предельный переход А, получаем
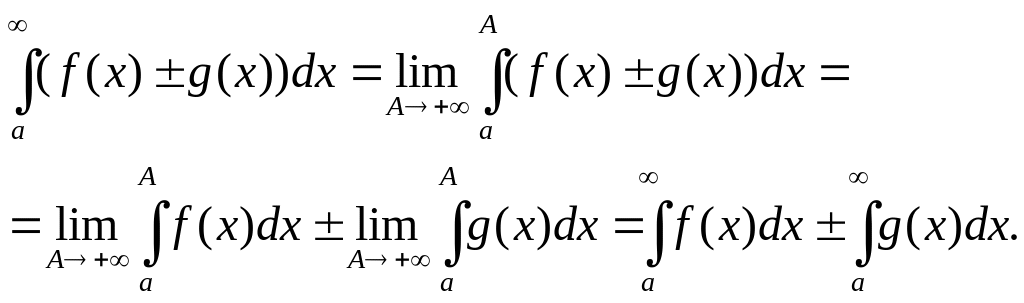
4. Если сходятся
и с
константа, то сходится и
и верна формула
.
Доказательство. Имеем
.
Делая предельный переход А, получаем
.
8.3 Сходимость несобственных интегралов первого рода от неотрицательных функций
Важнейшим элементом теории несобственных интегралов является следующий: надо, не вычисляя интеграла, ответить на вопрос, сходится он или нет. В конце концов, если он сходится, то его можно вычислить численно на ЭВМ, а вот если он расходится попытки сосчитать его численно ни к чему хорошему не приведут.
В данном разделе
мы рассмотрим вопрос о признаках
сходимость несобственных интегралов
первого рода от неотрицательных функций.
В дальнейшем будем предполагать, что
функции
и
.
Сформулируем основные результаты этого раздела в виде теорем.
Теорема 1. Для того, чтобы сходился, необходимо и достаточно, чтобы
.
Доказательство.
Рассмотрим функцию
.
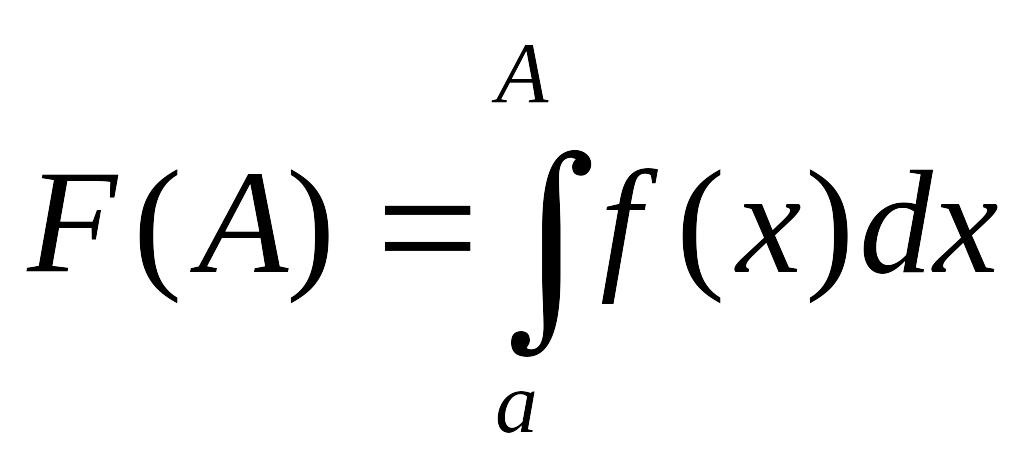В силу того, что
эта функция монотонно возрастает с
ростом А,
так как с ростом А
промежуток интегрирования увеличивается.
Но вспомним теорему о существовании
предела монотонно возрастающей функции
из главы 2. Согласно этой теореме, для
того, чтобы существовал конечный предел
необходимо и достаточно, чтобы эта
функция была ограничена сверху, то есть,
чтобы было выполнено условие
.
Но если заменить
его явным выражением мы как раз и получим
условие нашей теоремы.
Теорема
2. Пусть
.
Тогда
А) из сходимости следует сходимость ;
Б) из расходимости следует расходимость .
Доказательство.
А) Пусть сходится. Тогда, согласно теореме 1,
.
Но и поэтому
,
и, согласно той же теореме 1, сходится.
Б) Пусть
расходится. Так как
,
то это означает, что
.
Но, так как
,
то
,
и поэтому
,
что и означает,
что
,
то есть
расходится.
Теорема
3. Пусть
,
.
Тогда интегралы
и
сходятся или
расходятся одновременно.
Доказательство.
1. В формулировке теоремы сказано, что . Согласно определению предела это значит, что
.
(*)
2. Пусть
сходится. В (*) рассмотрим вторую половину
неравенства, которую запишем в виде
.
Тогда имеем следующую цепочку следований
(сообразите сами, где идет ссылка на
свойства несобственных интегралов и
где на теорему 2):
сходится
сходится
сходится
сходится
сходится.
3. Пусть теперь
сходится. Возьмем
настолько малым, чтобы было
.
Тогда из левого неравенства в (*) следует,
что
и мы имеем следующую цепочку следований
(и снова сообразите сами, где идет ссылка
на свойства несобственных интегралов
и где на теорему 2):
сходится
сходится
сходится
сходится
сходится.
Теперь мы имеем возможность доказать признак сходимости, который часто применяется при решении задач.
Практический признак сходимости.
Пусть
,
.
Тогда
сходится при
и расходится при
.
(Заметим, что вопрос о том, как же находить , остается на данном этапе открытым).
Доказательство.
Возьмем
функцию
в виде
.
Тогда условие теоремы 3 примет вид
,
и
сходится
или расходится одновременно с интегралом
.
Рассмотрим
поэтому вопрос о сходимости этого
интеграла.
1. Пусть
.
Тогда
.
Будут два варианта:
а)
.
В этом случае
,
поэтому
и
,
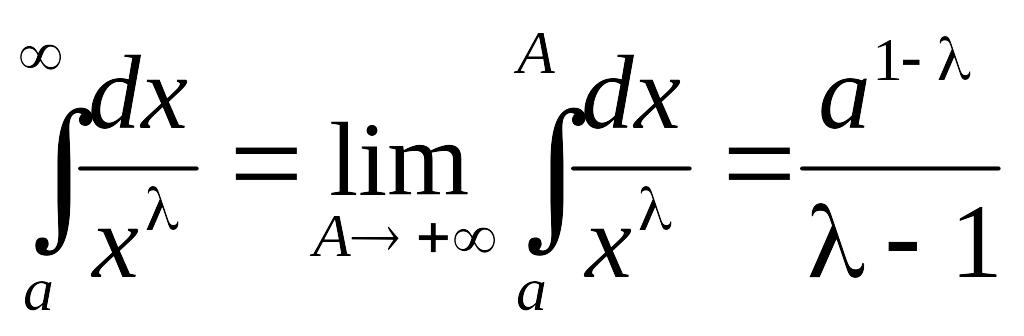так что
сходится.
б)
.
В этом случае
,
поэтому
и
,
так что расходится.
2. 
.
Тогда
,
так что
расходится.
Таким образом,
сходится
при
и расходится при
.
По теореме 2
также сходится при
и расходится при
.
Все упирается в нахождение величины . Как это делать будет разобрано на практике.