32. Алгоритм быстрого преобразования Фурье с прореживанием по частоте.

Вместо изложенной процедуры разбиения множества объектов на объекты с четны-

ми и нечетными номерами можно рассмотреть процедуру разбиения исходного множества на две половины: правую и левую. Последняя процедура и нашла применение в алгоритме БПФ, основанном на прореживании по частоте.

Пусть имеется исходная N - точечная последовательность x_n , где N = 2^M (рисунок 6.4). Разобьем члены этой последовательности на две группы. В первую включим первую половину членов исходной последовательности, а во вторую группу - вторую половину. Из первой группы образуем последовательность x1_m , а из второй - последовательность x2_m.

Рисунок 4.4 - Разбиение последовательности отсчетов x на две последовательности

x1 и x2, содержащие первую и вторую половину членов исходной

последовательности соответственно

Индексы последовательностей x_n и x1_m связаны соотношением n = m, а индексы по-

следовательностей x_n и x2_m - соотношением n = N/ 2 + m.

Тогда выражение для прямого ДПФ (6.3) можно представить в виде

.

Рассмотрим отдельно четные и нечетные отсчеты спектра (отсюда и название алгоритма: прореживание по частоте).

Для получения четных отсчетов спектра положим k = 2 i, где i = 0, 1, 2, . . N /2 -1.

В результате получим

.

Для получения нечетных отсчетов спектра положим k = 2i + 1, где i = 0, 1, 2, . . N/2-1.

Тогда

.

Два последних соотношения представляют собой N / 2 - точечные ДПФ последовате- льностей и .

Графическое представление операций для 8 - точечной последовательности показано на рисунке 4.5. Образовавшиеся после первого разбиения блоки ДПФ подвергаются дальнейшему разбиению подобно тому, как это делалось в предыдущем алгоритме с прореживанием во времени.

Оба алгоритма равноценны.

Рисунок 4.5- Формирование отсчетов спектра восьмиточечной последовательности

из отсчетов спектров двух четырехточечных последовательностей с

использованием прореживания по частоте

33. Оконное преобразование Фурье. Непрерывное вейвлет - преобразование.

Дискретизация непрерывного вейвлет-преобразования. Частотно-временная плоскость.

4.5. Дискретное косинусное преобразование

Дискретное преобразование Фурье имеет дело с комплексными числами. Каждое комплексное число хранится в памяти вычислителя в виде двух чисел, представляющих его действительную и мнимую части. Сложение двух комплексных чисел требует выполнения двух операций сложения, а умножение двух комплексных чисел – четырех операций умножения, из-за чего существенно увеличивается время вычислений. Последнее может служить препятствием для обработки широкополосных сигналов в реальном масштабе времени. Чтобы работать только с действительными числами используют дискретное косинусное преобразование (ДКП).

Прямое ДКП дискретного сигнала x_n, представленного выборкой из N отсчетов при n=0,1..N-1, определяется следующими соотношениями:

Обратное ДКП позволяет определить сигнал как функцию времени по известным коэффициентам С_k

Приведенные соотношения представляют одномерное ДКП. В цифровом телевидении для сжатия изображения применяют двумерное ДКП.

4.6.1. Вейвлет-преобразование аналогового сигнала

Недостатком прямого преобразования Фурье при анализе спектра сигнала является невозможность оценить характер изменения спектра во времени, т.к. при определении спектральной плотности интегрирование по времени осуществляется в пределах от

.

На рисунке 4.6 показан дискретный сигнал, представляющий собой сумму двух синусоидальных колебаний с одинаковыми амплитудами, но разными частотами, отличающимися друг от друга в 6 раз, а на рисунке 4.7 – их спектр, полученный методом БПФ.

Рисунок 4.6 – Сигнал в виде суммы двух синусоидальных колебаний

Рисунок 4.7 – Спектр сигнала, представленного на рисунке 6.6

На рисунке 4.8 приведена временная диаграмма дискретного сигнала, образованного теми же синусоидами, но действующими поочередно, а на рисунке 4.9 –его спектр.

Рисунок 4.8 – Сигнал, образованный двумя синусоидальными колебаниями,

действующими поочередно

Рисунок 4.9 – Спектр сигнала, представленного на рисунке 6.8

Из сравнения последних четырех рисунков следует, что сигналы, существенно отличающиеся друг от друга, имеют практически одинаковый спектр, полученный методом ДПФ.

Этот недостаток частично устраняется при использовании оконного преобразования Фурье, которое определяется следующим соотношением

,

где - оконная функция, - временной сдвиг оконной функции относительно начала координат (t = 0).

Сигнал x(t) и оконная функция показаны на рисунке 4.10. Типичной оконной функцией является функция Гаусса

.

С помощью оконной функции оценивается спектр сигнала на ограниченном временном интервале, а перемещение окна позволяет выявить временные характеристики спектра. Однако при использовании оконного преобразования Фурье возникает проблема выбора ширины окна. При малой ширине окна получается хорошее временное разрешение, но плохое частотное, при широком окне – наоборот. Возможности изменения ширины окна это преобразование не предоставляет. Кроме того базисными функциями оконного преобразования, как и обычного преобразования Фурье остаются гармонические функции, которые хорошо описывают плавно изменяющийся сигнал, но плохо приспособлены для выделения скачков сигнала.

Рисунок 4.10 – Анализируемый сигнал и оконная функция

Указанных недостатков лишено вейвлет - преобразование. Непрерывное вейвлет-преобразование аналогового сигнала x(t) определяется следующим соотношением

,

где - вейвлет.

В обозначении функции нижний индекс x соответствует анализируемой функции x(t), а верхний индекс – вейвлету .

Слово «вейвлет» означает маленькая волна. Эта волна имеет конечную длительность и может рассматриваться как оконная функция.

Параметрами этой функции являются: - параметр сдвига относительно начала координат, s – параметр масштаба, определяющий ширину вейвлета. Большие значения масштаба позволяют получить глобальное представление о сигнале, а малые значения позволяют различать детали. При и s = 1 вейвлет называется материнским вейвлетом.

Материнский вейвлет должен удовлетворять условию

Существует большое количество различных вейвлетов. На рисунках 4.11 и 4.12 показан вейвлет «Мексиканская шляпа» при различных значениях параметров и s. Этот вейвлет описывается следующим соотношением

.

Рисунок 4.11 – Вейвлет “Мексиканская шляпа” при разных значениях параметра s

Рисунок 4.12 – Вейвлет “Мексиканская шляпа” при разных значениях параметра

Процедура анализа сигнала стартует с масштаба s = 1. Вейвлет сначала помещается в начало координат, умножается на сигнал и результат умножения интегрируется на всем временном интервале. Затем он сдвигается вправо на величину τ и описанная процедура повторяется. Затем масштаб увеличивается и снова осуществляется перемещение вейвлета вдоль оси времени.

Значение s = 1 соответствует сжатому вейвлету и позволяет выявить высокочастотные составляющие сигнала. Большие значения масштаба выделяют низкочастоные составляющие сигнала.

Реконструкция сигнала по его вейвлет-преобразованию осуществляется по формуле

где

.

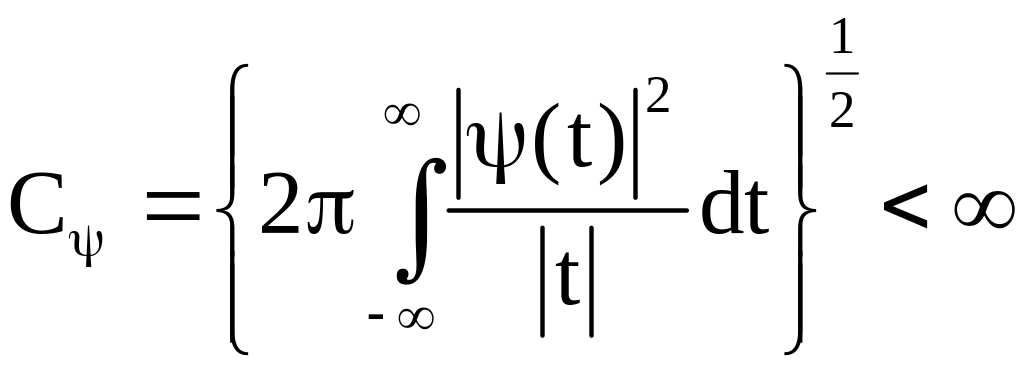4.6.2.Дискретизация непрерывного вейвлет-преобразования

Для осуществления непрерывного вейвлет-преобразования на ЭВМ необходимо задавать дискретные значения параметров вейвлета s и . На рисунке 4.13 точками показаны дискретные значения этих параметров. По оси ординат вместо s для удобства отложена величина логарифма s по основанию 2. Интуитивно понятно, что чем шире вейвлет, тем больше можно выбрать шаг изменения . На рисунке s = 1,2,4,8.., и при каждом удвоении масштаба интервал дискретизации увеличивается также в 2 раза. Плоскость, представленную на рисунке, принято называть частотно-временной плоскостью, т.к. масштаб s связан с частотой анализируемого сигнала: большему масштабу соответствуют более низкие частоты.

Рисунок 4.13 – Частотно-временная плоскость

Дискретизацию масштаба можно представить следующим образом

.

Тогда дискретизация сдвигов осуществляется в соответствии с соотношением

,

где k –целое число.

При этом вейвлет описывается функцией

.

С учетом последнего соотношения вейвлет-преобразование для дискретных значений параметров описывается следующим соотношением

,

где

.

На рисунках 4.14, 4.15 и 4.16 показаны сигнал и его вейвлет-преобразование. Вейвлет-преобразование представлено в трёхмерной системе координат (рисунок 4.15) и картой линий уровня (рисунок 4.16) в системе координат «сдвиг-частота» с учетом того, что уменьшению масштаба соответствует увеличение частоты. Линией уровня называется линия, вдоль которой величина функции, заданной на плоскости двух переменных, остается постоянной. На рисунке 4.17 показан увеличенный фрагмент карты линий уровня, на котором проставлены значения функции, например, 0.5, 1, -0.5.

Одновременному существованию двух синусоидальных колебаний соответствует однородная во времени структура вейвлет-преобразования с выраженными периодами, соответствующими низкочастотной и высокочастотной синусоидам.

Рисунок 4.14 – Сигнал, образованный суммой двух синусоидальных

колебаний

Рисунок 4.15 - – Вейвлет-преобразование сигнала, представленного

на рисунке 6.14, в трёхмерной системе координат

Рисунок 4.16 – Вейвлет-преобразование сигнала, представленного

на рисунке 6.14, в виде карты линий уровня

На рисунках 4.18, 4.19 и 4.20 показаны временная диаграмма и вейвлет - преобразование для случая, когда два синусоидальных колебания действуют во времени последовательно.

Переходу от низкочастотной к высокочастотной синусоиде соответствует резкое изменение во времени структуры вейвлет - преобразования. Таким образом, информативность вейвлет - преобразования значительно выше информативности преобразования Фурье.

Рисунок 4.18 - Сигнал, образованный двумя синусоидальными колебаниями,

действующими поочередно

Рисунок 4.19 - Вейвлет-преобразование сигнала, представленного

на рисунке 4.18, в трёхмерной системе координат