Наибольшее и наименьшее значение функции на отрезке.

Говорят, что функция , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство .

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке :

1. найти ;

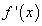2. найти точки, в которых или не существует, и отобрать из них те, что лежат внутри отрезка ;

3. вычислить значения функции в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции на отрезке , которые можно обозначить так: .

Выпуклость графика функции. Точки перегиба.

Точка перегиба функции внутренняя точка области определения , такая что непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

Необходимое условие существования: если функция f(x), дважды дифференцируемая в некоторой окрестности точки , имеет в точку перегиба, то .

Достаточное условие существования: если функция в некоторой окрестности точки раз непрерывно дифференцируема, причем нечётно и , и при , а , то функция имеет в точку перегиба.

Выпуклость. Если для любых точек x ₁ и x ₂ отрезка [ a ;  b ] секущая AB проходит под графиком функции f  ( x ), то функция f выпукла вверх.

Аналогично определяется функция, выпуклая вниз.

функция f ( x ) выпукла вверх, если для любого

Асимптоты. Общая схема исследования функций.

Аси́мпто́та^[1] (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность

1. 1. Найти ОДЗ и точки разрыва функции.

   2. Найти точки пересечения графика функции с осями координат.

2. Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

3. Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

4. Найти асимптоты графика функции: а) вертикальные, b) наклонные.

5. На основании проведенного исследования построить график функции.

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов

3. Нахождение двух пределов :

если в п. 2.), то , и предел ищется по формуле горизонтальной асимптоты, .

Формула Тейлора и Маклорена

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

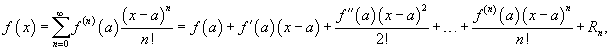
где R_n − остаточный член в форме Лагранжа определяется выражением

Если приведенное разложение сходится в некотором интервале x, т.е. , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: