Правило Лопиталя.

Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или . Пусть a является некоторым конечным действительным числом или равно бесконечности.

• Если и , то ;

• Если и , то аналогично .

Это правило впервые упоминалось в книге по дифференциальному исчислению, опубликованной в 1696 году французским математиком Гийомом Лопиталем (1661- 1704).

Правило Лопиталя можно также применять к неопределенностям типа

Точки разрыва функции и их классификация..

Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел и правосторонний предел ;

• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу: Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу: Такая точка называется точкой конечного разрыва.

Модуль разности значений односторонних пределов называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Комплексные числа. Формы записи комплексного числа

Ко́мпле́ксные чи́сла (устар. Мнимые числа), — расширение поля вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и  — вещественные числа,  — мнимая единица

Запись комплексного числа в виде , , называется алгебраической формой комплексного числа

Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент ( , ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме

Пусть  — комплексное число, где и  — вещественные числа. Числа или и или называются соответственно вещественной и мнимой (аналогично англ. real, imaginary) частями .

• Если 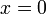, то называется мнимым или чисто мнимым числом.

• Если , то является действительным (вещественным) числом.

Основные теоремы о пределах.

• Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

 .

• Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

 .

• Теорема 3. Предел постоянной равен самой постоянной.

.

• Теорема 4. Функция не может иметь двух различных пределов в одной точке.

• Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов.

.