Завдання 2. Використання методу вибіркового спостереження для визна- чення частки досліджуваної ознаки в певній сукупності
Мета завдання: Навчитися розрахувати чисельні характеристики статистичної сукупності на основі методу вибіркового спостереження
Зміст завдання: У відповідності із варіантом завдання розрахувати за допомогою методу вибіркового спостереження визначити:
c) частку робітників, неперервний стаж роботи яких на даному підприємстві перевищує 20 років, при умові, щоб гранична похибка вибірки не перевищувала 5% з ймовірністю 0,89;
Послідовність виконання завдання
1)
Таблиця 4.5
Генеральна сукупність даних для дослідження неперервного стажу роботи
№ з\п |
Неперервний стаж |
№ з\п |
Неперервний стаж |
№ з\п |
Неперервний стаж |
1 |
8 |
54 |
10 |
107 |
9 |
2 |
8 |
55 |
1 |
108 |
5 |
3 |
13 |
56 |
23 |
109 |
9 |
4 |
13 |
57 |
17 |
110 |
11 |
5 |
15 |
58 |
18 |
111 |
15 |
6 |
2 |
59 |
25 |
112 |
5 |
7 |
3 |
60 |
11 |
113 |
1 |
8 |
5 |
61 |
23 |
114 |
1 |
9 |
9 |
62 |
21 |
115 |
1 |
10 |
6 |
63 |
23 |
116 |
21 |
11 |
8 |
64 |
9 |
117 |
5 |
12 |
10 |
65 |
30 |
118 |
13 |
13 |
4 |
66 |
7 |
119 |
32 |
14 |
2 |
67 |
1 |
120 |
24 |
15 |
8 |
68 |
12 |
121 |
1 |
16 |
7 |
69 |
18 |
122 |
4 |
17 |
7 |
70 |
9 |
123 |
16 |
18 |
11 |
71 |
22 |
124 |
4 |
19 |
21 |
72 |
18 |
125 |
17 |
20 |
10 |
73 |
14 |
126 |
17 |
21 |
20 |
74 |
10 |
127 |
10 |
22 |
2 |
75 |
15 |
128 |
34 |
23 |
18 |
76 |
1 |
129 |
1 |
24 |
13 |
77 |
15 |
130 |
7 |
25 |
13 |
78 |
3 |
131 |
9 |
26 |
12 |
79 |
2 |
132 |
17 |
27 |
4 |
80 |
2 |
133 |
1 |
28 |
10 |
81 |
7 |
134 |
16 |
29 |
7 |
82 |
15 |
135 |
15 |
30 |
8 |
83 |
5 |
136 |
6 |
31 |
7 |
84 |
13 |
137 |
2 |
32 |
5 |
85 |
19 |
138 |
13 |
33 |
4 |
86 |
15 |
139 |
7 |
34 |
9 |
87 |
22 |
140 |
13 |
35 |
26 |
88 |
3 |
141 |
6 |
36 |
12 |
89 |
6 |
142 |
26 |
37 |
19 |
90 |
3 |
143 |
10 |
38 |
11 |
91 |
9 |
144 |
15 |
39 |
17 |
92 |
17 |
145 |
14 |
40 |
19 |
93 |
13 |
146 |
18 |
41 |
10 |
94 |
2 |
147 |
11 |
42 |
5 |
95 |
7 |
148 |
20 |
43 |
1 |
96 |
2 |
149 |
6 |
44 |
15 |
97 |
13 |
150 |
15 |
45 |
1 |
98 |
28 |
151 |
12 |
46 |
20 |
99 |
4 |
152 |
19 |
47 |
14 |
100 |
9 |
153 |
1 |
48 |
4 |
101 |
10 |
154 |
5 |
49 |
3 |
102 |
21 |
155 |
2 |
50 |
16 |
103 |
3 |
156 |
24 |
51 |
5 |
104 |
13 |
157 |
6 |
52 |
7 |
105 |
18 |
158 |
34 |
53 |
5 |
106 |
5 |
159 |
12 |
2) Обсяг вибірки визначається при:
без повторному відборі: повторному відборі:
n
=
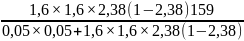= -1336,88/-8,41= 158,96 n
=
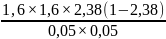= -3363,22
де N – обсяг генеральної сукупності;
Bx – гранична похибка вибірки для заданої ймовірності Р;
t – довірче число (коефіцієнт довіри) для заданого значення ймовірності
Р (визначається на основі табличних даних Додатку В); 1,6
w – частка одиниць сукупності, які мають певні значення ознаки (w = 2,38
m/n, де m – кількість одиниць, які мають певні значення ознаки, n = 8);
(1-w) – частка одиниць сукупності із протилежним значенням ознаки;
w(1-w) – дисперсія частки, значення якої можна розрахувати за результа-
тами завдання 1 лабораторної роботи № 1.
3)
Таблиця 4.6