1.3. Дс на площині

Крім просторових ДС також використовуються ДС на площині. Їх можна отримати як перерізи просторових ДС (рис. 1.8 та рис. 1.9), а також безпосередньо ДС на площині розділяються на 2 основні види: в полярній системі або прямокутній.

ДС в полярній системі. ДС в полярній системі являються досить наглядними. Вони фактично аналогічні перерізу просторових ДС в сферичній системі.

Ln=0.48;

subplot (2,3,1); v=0:pi/50:2*pi;

bi=2*pi*Ln; b2=cos(b1); b3=cos (b1.*cos(v))-b2;

b4=(1-b2).*sin(v); F=abs(b3./b4); polar (v,F);

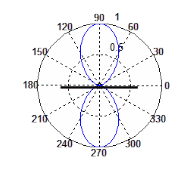
Рис. 1.11. ДС СВ в полярній системі при: Ln=0.48;

ДС в прямокутній системі. Такі ДС являються менш наглядними, порівняно з ДС в полярній системі. Але дозволяють розглянути більш «тонку» структуру ДС, наприклад, розглянути пелюстку шириною в декілька градусів.

Ln=0.48;

subplot (2, 3, 1) ; va=-180; vb=180; n=115;

var=va*pi/180;vbr=vb*pi/180;vba=(vbr-var)/n;

v =var:vba:vbr; v1=v.*180./pi;

b1=2*pi*Ln;b2=cos(b1);b3= cos( b1.*cos(v))-b2;

b4=(1-b2).*sin(v);a1=b3./b4; F=abs(a1); plot(v1,F);

grid on; hold on ; axis([va vb 0 1.1 ]);

xlabel('v'); ylabel('F');

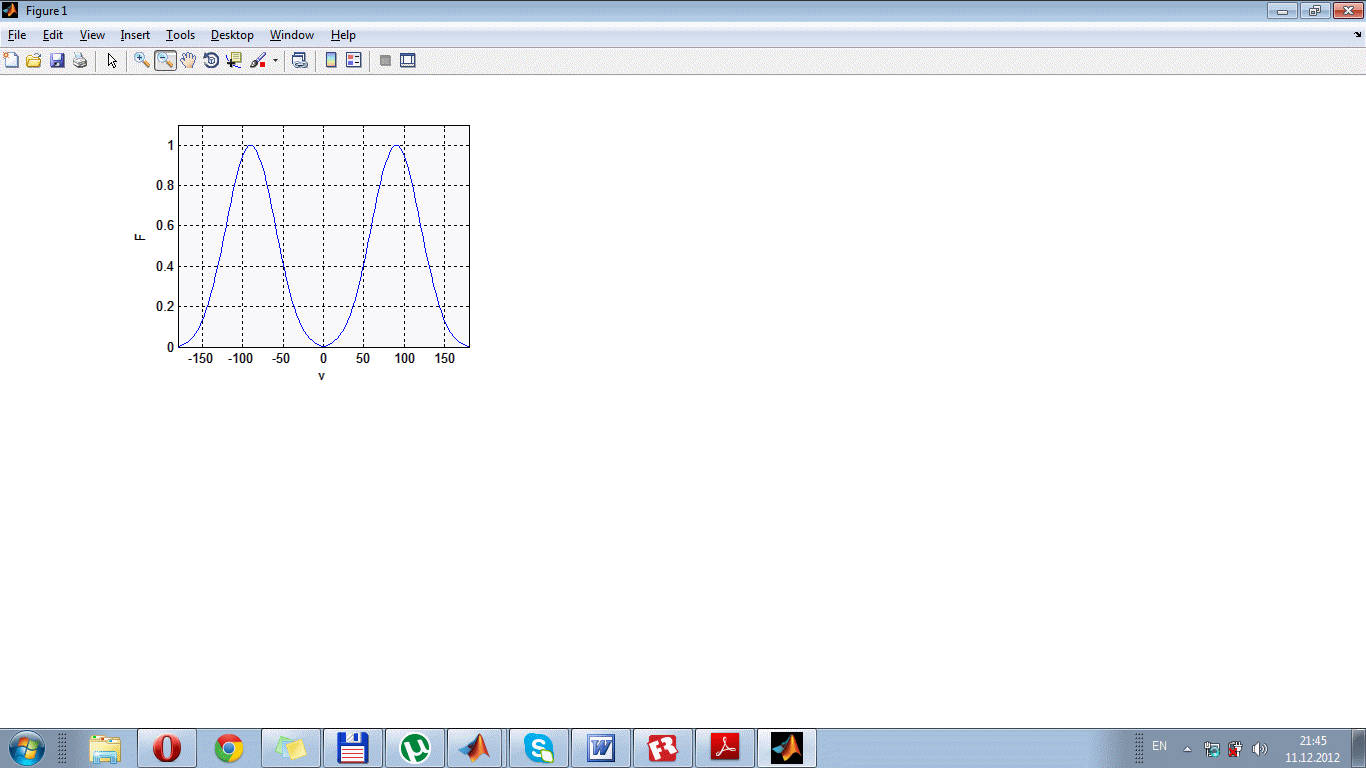
Рис. 1.12. ДС СВ в прямокутній системі при Ln=0.48.

На основі отриманих результатів можна зробити ряд висновків:

• ДС СВ може містити в межах кута 0< V< pi одну головну пелюстку або декілька, причому для практичних застосувань доцільно використовувати тільки ДС з однією головною пелюсткою, тобто при Ln < 0.7;

• СВ (при Ln < 0.7) являється антеною поперечного випромінювання - напрям головної пелюстки нормальний до осі СВ;

• при збільшенні Ln (в межах від 0.25 до 0.7) ШГП зменшується;

• при Ln>0.5 наявні бокові пелюстки, які зростають при збільшенні Ln;

• найбільш доцільно використовувати СВ при Ln=5/8=0.625, де ШГП вже досить вузька, а рівень бокових пелюсток ще незначний.

2. Визначення ширини головного пелюстка.

Одним з найбільш важливих параметрів при дослідженні антен являється ШГП. Вона визначається кутом в межах головної пелюстки ДС, де зосереджена певна частина (переважно половина, яка позначається 2θ_0.5) всієї потужності випромінювання. Тому, у випадку використання нормованої ДС за потужністю, (напруженістю) межами ШГП являється область, для якої Fр>0.5 (F_E>0.7).

2.1. Використання дс на площині.

Одним з шляхів визначення ШГП являється використання ДС на площині.

ДС в полярній системі. Для визначення ШГП при використанні нормованої ДС в полярній системі необхідно побудувати допоміжне коло : радіусом 0.7 або 0.5 - при наявності ДС за напруженістю поля або потужністю, відповідно.

Ln=0.48;

subplot(2,3,1); v = 0:pi/50:2*pi;

b1=2*pi*Ln; b2=cos(b1); b3=cos( b1.*cos(v))-b2;

b4=(1-b2).*sin(v); F=abs(b3./b4); polar (v, F);

hold on; F1=v./v; polar(v,0.7*F1);

Р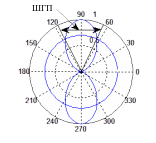 ис. 2.1. Визначення ШГП на основі ДС СВ в полярній системі при Ln=0.48

Точки перетину ДС та допоміжного кола являються основою для побудови сторін кута, який визначає ТИПІ. Видно, що ШГП становить, орієнтовно: 60° при Ln=0.48

ДС в прямокутій системі. Для визначення ШГП при використанні нормованої ДС в прямокутній системі необхідно побудувати допоміжну пряму: на рівні 0.7 або 0.5 — при наявності ДС за напруженістю поля або потужністю, відповідно.

Ln=0.48;

subplot (2,3,1); va=-180; vb=180; n=115;

var =va*pi/180; vbr =vb*pi/180; vba =(vbr-var)/n ;

v =var:vba:vbr; v1=v.*180./pi;

b1=2*pi*Ln;b2=cos (b1) ;b3= cos (b1.*cos(v) )-b2;

b4= (1-b2).*sin(v) ; a1=b3./b4; F=abs(a1); plot (v1, F);

hold on ;plot(v1,0.7*v1./v1);

grid on; hold on; axis ([va vb 0 1.1 ]);

xlabel('v'); ylabel('F ');

Рис. 2.2. Визначення ШГП на основі ДС СВ в прямокутній системі при Ln=0.48;

Видно, що ШГП становить, орієнтовно: 53⁰ при Ln=0.48.

Варто зауважити, що у випадку використання ДС в прямокутній системі можна більш точно визначити значення ШГП, збільшивши масштаб по горизонтальній осі.

Рис. 2.3. Визначення ШГП на основі ДС СВ в прямокутній системі при Ln=0.48;

Видно, що в даному випадку можна дещо точніше визначити значення ШГП.