Міністерство освіти, науки, молоді та спорту України

Національний університет «Львівська політехніка»

Розрахунково-графічна робота з курсу «Антенно-фідерні пристрої систем зв’язку»

Виконала:

ст. гр. ТК-32

Мельник Ганна

Львів 2012

Зміст

1. Симетричний вібратор та його ДС 3

1.1. Будова СВ та визначення ДС 3

1.2. Просторова ДС в сферичній системі та її перерізи. 6

1.3. ДС на площині 9

2. Визначення ШГП 11

2.1. Використання ДС на площині. 11

2.2. Застосування методу 2D-3D-2D^/ 13

3. Дослідження впливу нормованої довжини плеча СВ на форму ДС. 15

3.1. Комбіновані ДС в прямокутній системі. 15

3.2. Комбіновані ДС в сферичній системі. 17

4. Висновок 21

1. Симетричний вібратор та його діагональ спрямованості.

СВ являється ніби логічним розширення диполя Герца, але таку антену вже можна реалізувати практично. Він складається з двох плеч, кожне довжиною L, які розташовані вздовж прямої лінії. Саме нормована (відносно довжині хвилі λ) довжина

Ln=L/λ (1.1)

визначає, в основному, показники симметричного вібратора.

1.1. Будова св та визначення дс.

Будова. СВ складається з двох ідентичних металевих стержнів (або плеч СВ), кожне з яких характеризується довжиною L та поперечним перерізом S.

Плеча розміщені вздовж однієї прямої (осі вібратора) з невеликою віддаллю між ними, причому значення вказаної віддалі практично не впливає на показники СВ. Між найближчими точками обох пліч вмикається передавач, або приймач, причому сигнал в даній точці характеризується струмом І.

1) СВ:L 2) CB: кут , точка спостереження М

Вимоги до розмірів. Для забезпечення форми ДС СВ, необхідної для ефективного функціонування СВ в складі радіомережі, геометричні розміри СВ не можуть бути довільними, причому визначальними являються не абсолютні значення розмірів – а їхні нормовані ) відносно довжини хвилі значення).

Простішим являється визначення вимог до розмірів поперечного перерізу

Sn=S/λ<<1 (1.2)

Тобто особливі вимоги до значення S відсутні. Варто зауважити, що на розміри S звертають увагу лише при проектуванні широкодіапазонних СВ. Саме тоді для зменшення впливу зміни робочої частоти на зміну вхідного опору СВ значення S необхідно збільшувати.

Більш складним являється визначення вимог до довжини плеча СВ. Справа в тому, що в залежності від довжини L, а точніше - її нормованого значення Ln (1.1) суттєво залежить ДС СВ. Як буде показано далі, для ефективного функціонування СВ в складі радіосистем, його нормована довжина повинна становити оптимальне значення L_nнорм =0.625. В окремих випадках, при необхідності, допускається використання СВ з меншою (але не більшою від оптимального значення ) нормованою довжиною плеча, яка може знаходись в межах

0.25<Ln< 0.625.

Струми в СВ. В зв'язку з розміщенням СВ (рис. 1.2) вздовж осі OZ (симетрично відносно її початку), для кінця довжини плеча СВ виконується умова

|z|=L (1.3)

Враховуючи те, що струм на кінцях СВ (не підімкнених до зовнішніх пристроїв) обовязково повинен бути рівним нулю, отримаємо розподіл струму в кожному з пліч СВ.

І=І_nsin[k(L-z)] (1.4)

де; Іn- амплітуда струму; k=2*pi/λ.

Струми (1.4) в кожному з пліч СВ являються симетричними відносно його середини та суттєво залежать від значення нормованої довжини L_n.

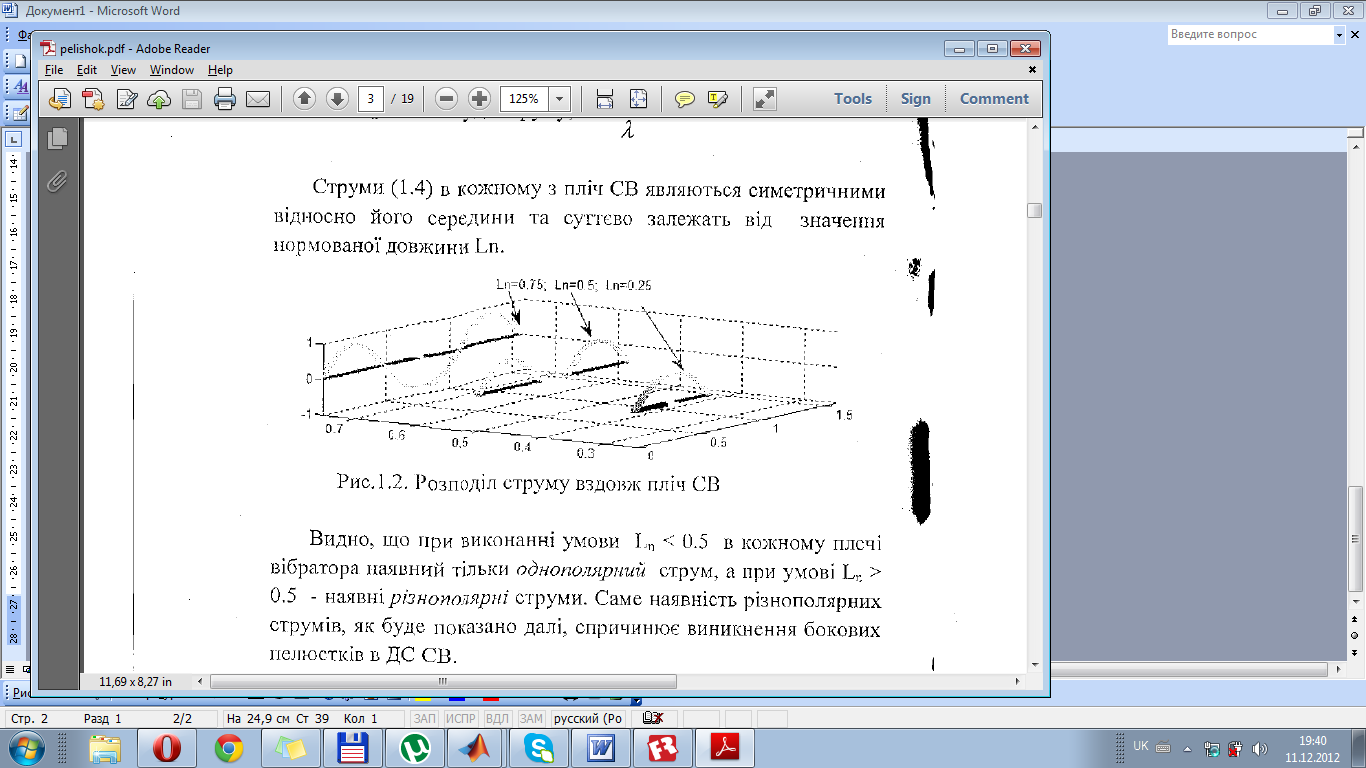
Видно, що при виконанні умови Ln < 0.5 в кожному плечі вібратора наявний тільки однополяртш струм, а при умові Ln > 0.5 - наявні різнополярні струми. Саме наявність різнополярних струмів, як буде показано далі, спричинює виникнення бокових пелюстків в ДС СВ.

Діаграма спрямованості СВ. На перший погляд основними чинниками, що впливають па ДС СВ, можуть бути : кути θ, φ сферичної системи координат; довжина плеча L, (значення S в зв'язку з його малим розміром не повинно впливати на форму ДС); довжина хвилі λ

.

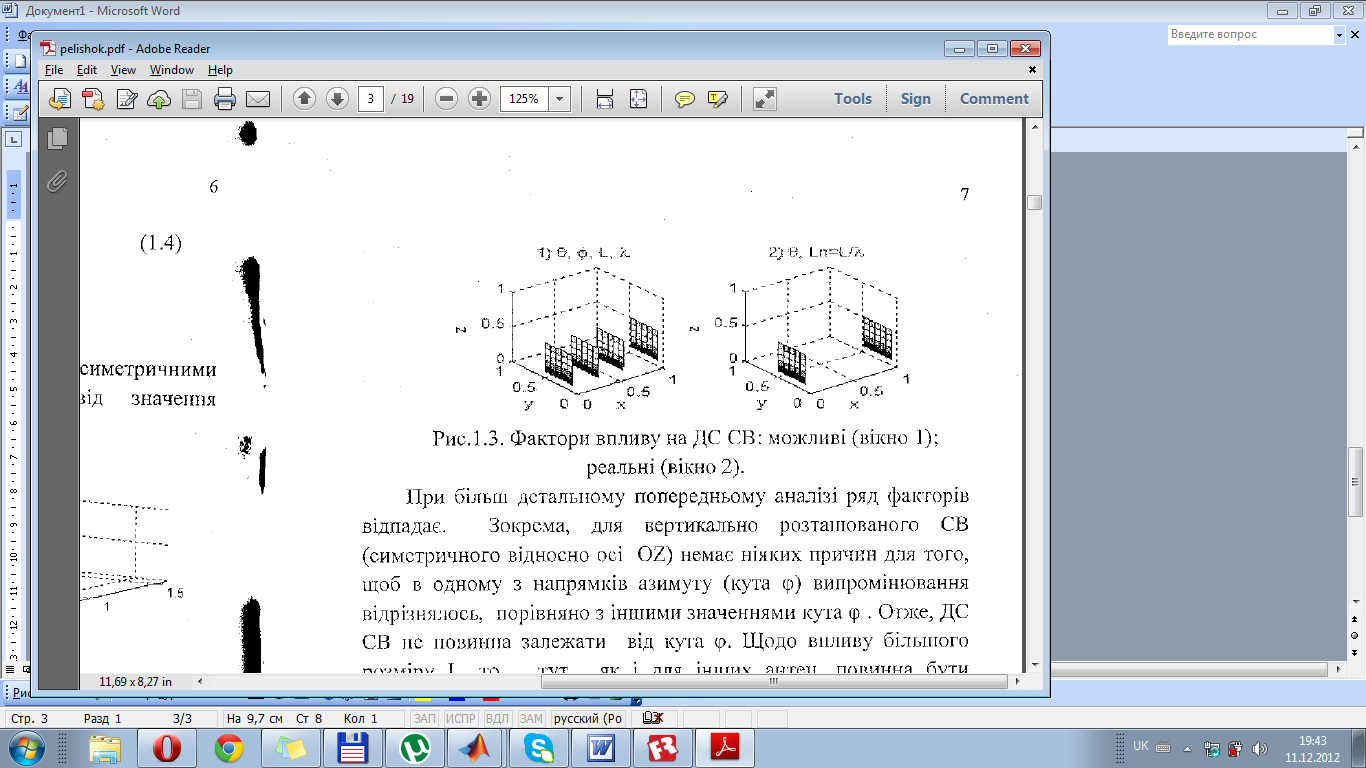
При більш детальному попередньому аналізі ряд факторів відпадає. Зокрема, для вертикально розташованого СВ (симетричного відносно осі OZ) немає ніяких причин для того, щоб в одному з напрямків азимуту (кута φ) випромінювання відрізнялось, порівняно з іншими значеннями кута φ . Отже, ДС СВ не повинна залежати від кута φ. Щодо впливу більшого розміру L, то тут , як і для інших антен, повинна бути справедлива наступна залежність: на форму ДС впливають не абсолютні геометричні розміри антен, а їх нормовані (відносно довжини хвилі) значення (1.1).

Отже, слід очікувати (рис. 1.4, вікно 2), що ДС для СВ повинна залежати лише від двох наступних параметрів: θ, L_n. Враховуючи те, що ДС більшості антен описуються тригонометричними функціями, тому ДС повинна залежати від значення L_n поданому в радіанах, тобто 2pi L_n.

Реально ненормована ДС СВ за напруженістю поля [1] становить:

(1.5)

У зв’язку з використанням програми Matlab часто застосовуються наступні позначення: θ=v, φ=g.

Отже, ДС для СВ дійсно залежить, як і передбачалось, від двох аргументів: кута θ сферичної системи та нормованої довжини L_n плеча СВ, причому при L_n наявний множник 2pi .

Просторова ДС СВ. Отримаємо просторове зображення ДС СВ.

Ln=0.48;

subplot(2,4,1); ga=0; gb=360; va=0; vb=180; n=15;

gar=ga*pi/180; gbr=gb*pi/180; var=va*pi/180;

vbr=vb*pi/180; gba=(gbr-gar)/n; vba=(vbr-var)/n;

[g,v]=meshgrid(gar:gba:gbr,var:vba:vbr);

b1=2*pi*Ln; b2=cos(b1); b3=cos(b1.*cos(v))-b2;

b4=sin(v);a1=b3./b4; fn=a1;

x=fn.*sin(v).*cos(g);y=fn.*sin(v).*sin(g);

z=fn.*cos(v);surf(x,y,z); grid on; hold on;

t = 0:0.01:2.4;

plot3(t./t-1,t./t-1,t-1.2, 'LineWidth',2); hold on;

xlabel('x'); ylabel ('y'); zlabel('z');

axis([-2 2 -2 2 -2 2]);

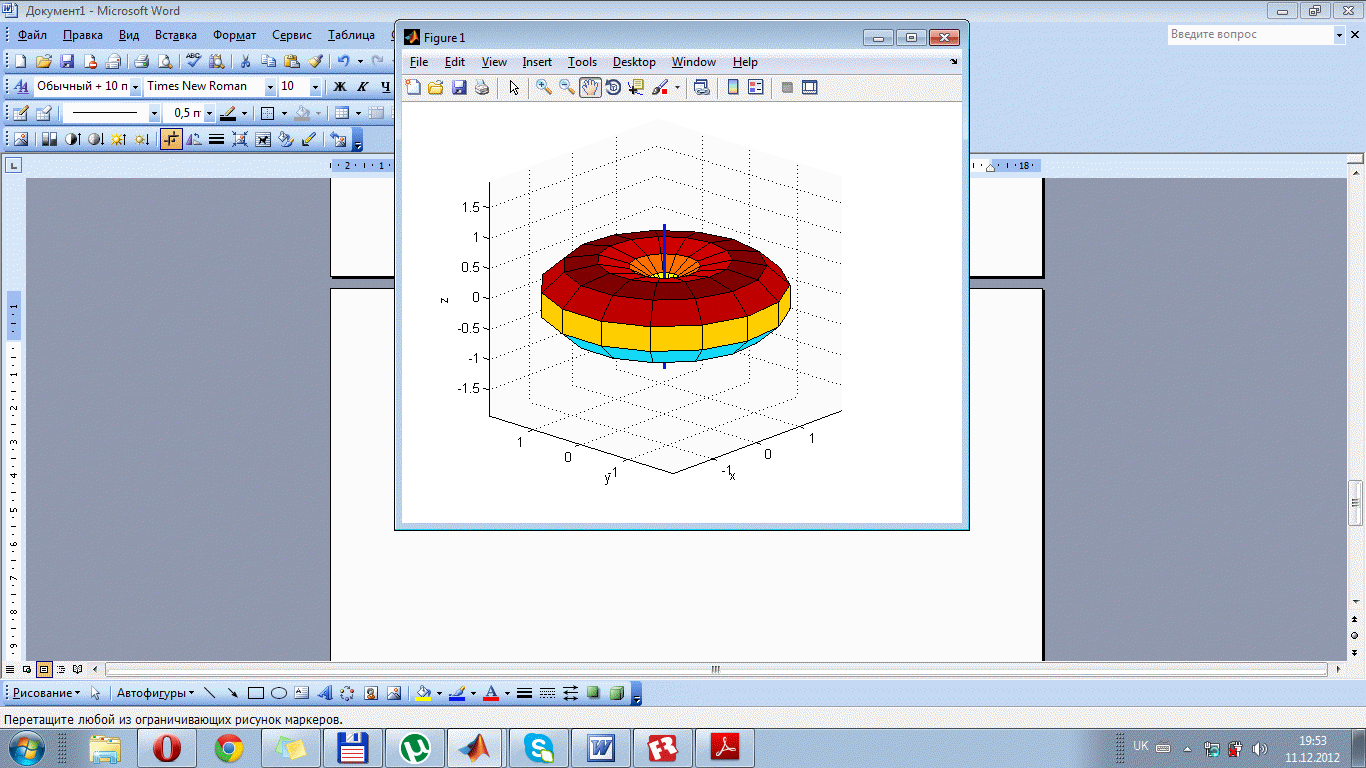
Рис. 1.4. Просторона ДС СВ: при Ln=0.48

При збільшенні Ln напрям максимального випромінювання зростає. Причому головна пелюстка роздвоюється на дві окремі, що являється не бажаним.

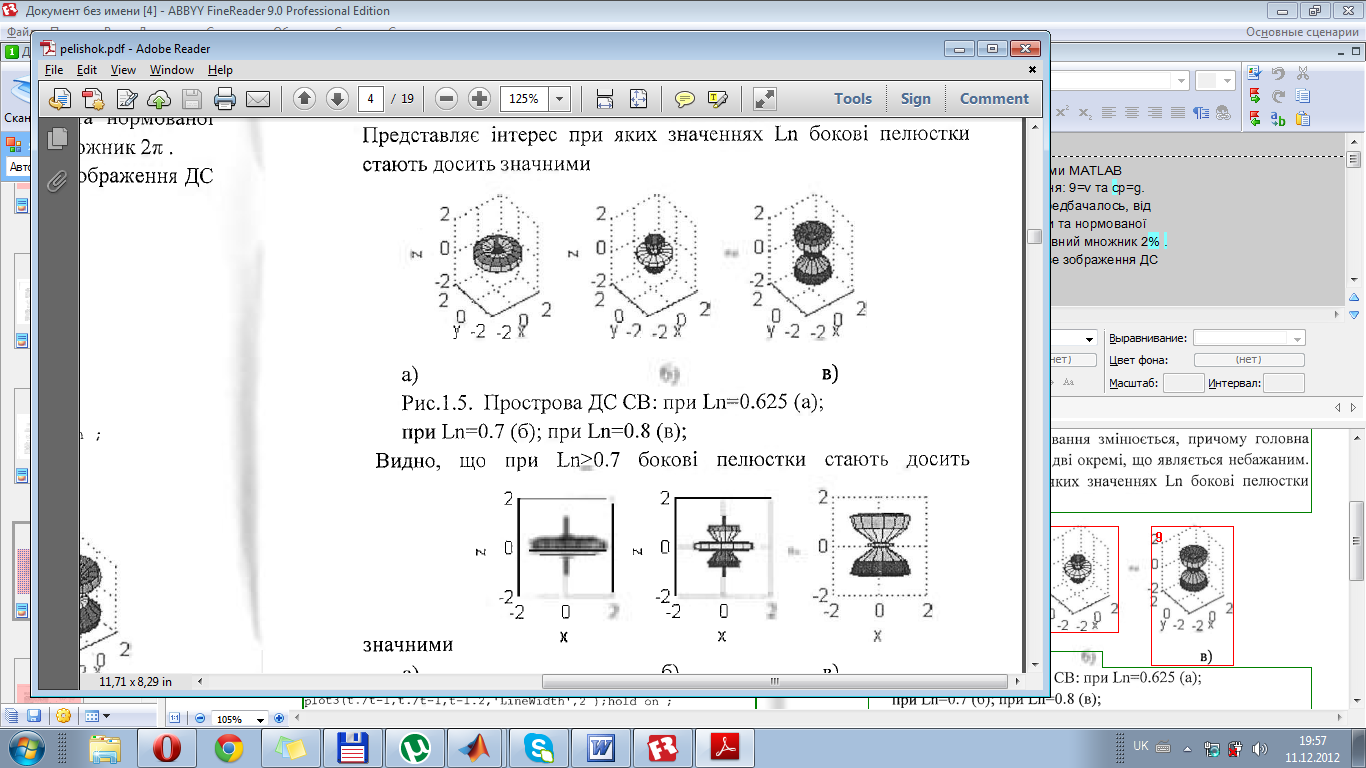
Видно, що при Ln≥0.7 бокові пелюстки стають досить значними:

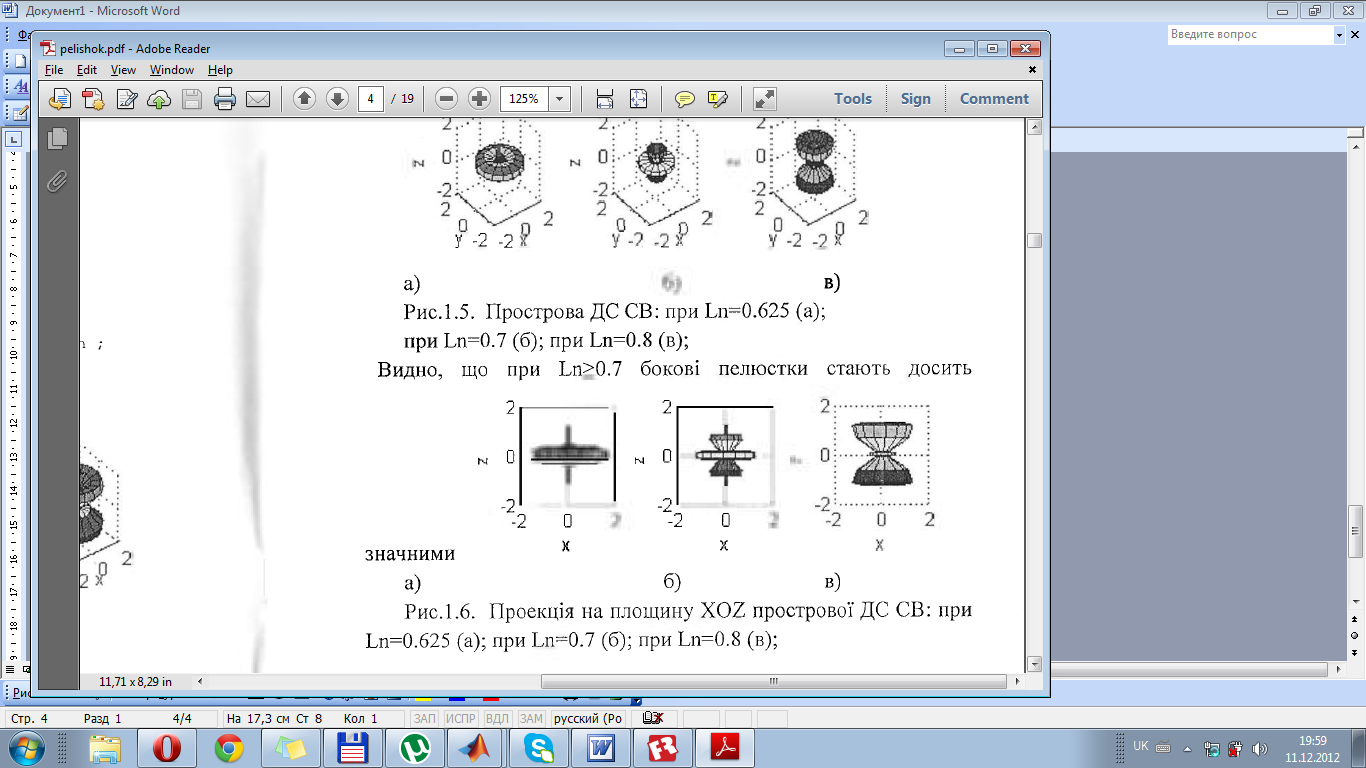
З приведених даних видно, що при Ln<0.7 напрям максимального випромінювання продовжує зберігатись нормальним до осі СВ. Але практично, найбільш часто, використовується СВ при умові Ln=Ln_опт=0.625, де рівень бокових пелюсток ще незначний, а ширина головної пелюстки (ШГП) вже досить мала.

Нормована ДС та її часткові випадки. При аналізі антен, особливо при їх порівнянні між собою, більш зручно використовувати нормовану ДС (відносно її максимального значення). Прийнявши в ДС (1.5) кут напрямку максимального випромінювання θ=pi/2 (що справедливо при Ln<0.7) отримаємо її максимальне значення f_max=(1- cos 2piLn) .

Отже, нормована ДС СВ становить [2]

при Ln<0.7 (1.6)

Далі будемо використовувати нормоване значення ДС СВ.