7.Системи лінійних рівнянь

Рівняння з n невідомими х₁,х₂,…,х_п називається лінійним, якщо його можна подати у вигляді: а₁х₁+а₂х₂+…+ а_пх_п= b , (1.1),де а₁,а₂,…,а_п– коефіцієнти, b – вільний член рівняння (дійсні числа).

Розв’язком системи лінійних рівнянь називається така сукупність записаних у певному порядку чисел 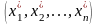, що кожне з рівнянь системи перетворюється на правильну рівність після заміни в ньому невідомих х_і відповідними числами (і=1,2,…,п).

Система лінійних рівнянь, яка має розв’язки, називається сумісною; система, яка не має жодного розв’язку, називається несумісною.

Сумісна система лінійних рівнянь називається визначеною, якщо вона має тільки один розв’язок, і невизначеною, якщо кількість її розв’язків більше одного.

Системи лінійних рівнянь називаються еквівалентними, якщо множини їх розв’язків збігаються.

Лінійне рівняння (1.1) називається неоднорідним, якщо його вільний член не дорівнює нулю, і однорідним, якщо вільний член дорівнює нулю.

Аналогічно, система лінійних рівнянь називається однорідною, якщо всі її рівняння однорідні.

Способи розв’язування систем лінійних рівнянь

а) Метод Гаусса розв’язування систем лінійних рівнянь (або метод послідовного виключення невідомих.)

Перетворення системи лінійних рівнянь у ступінчасту систему називають зведенням системи лінійних рівнянь до ступінчастого вигляду.

Теорема 1. Система лінійних рівнянь сумісна тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій немає рівнянь вигляду 0=b, де b≠0.

Теорема 2. Система лінійних рівнянь є визначеною тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій число рівнянь r дорівнює числу невідомих n.

Наслідок 1. Система лінійних рівнянь з п невідомими є визначеною тоді і тільки тоді, коли вона зводиться до ступінчастої системи, в якій

Наслідок 2. Сумісна система m лінійних рівнянь з п невідомими при m<n є невизначеною.

Випадок однорідної системи

Лінійне рівняння а₁х₁+а₂х₂+…+а_пх_п=b називається однорідним, якщо його вільний член b дорівнює нулю. Система лінійних рівнянь називається однорідною, або системою лінійних однорідних рівнянь, якщо всі її вільні члени рівні нулю.

Лінійно незалежна система розв’язків системи лінійних однорідних рівнянь називається фундаментальною, якщо кожний розв’язок однорідної системи є лінійною комбінацією цієї лінійно незалежної системи.

б) Метод Крамера розв’язування систем лінійних рівнянь

Якщо визначник d системи n лінійних рівнянь з n невідомими відмінний від нуля, то система має єдиний розв’язок: , де – визначник, отриманий із визначника d заміною його j-го стовпчика стовпчиком вільних членів системи.

Отримані формули розв’язку називають формулами Крамера, а саму теорему – правилом Крамера.

Наслідок. Система n лінійних однорідних рівнянь з п невідомими тоді і тільки тоді має розв’язки, відмінні від нульового, коли визначник цієї системи дорівнює нулю.

в) Матричний метод розв’язування систем лінійних рівнянь

Поняття оберненої матриці

Матриця А^-1 називається оберненою для квадратної матриці А, якщо АА^-1=А^-1А=Е. Тут Е – одинична матриця.

Матриця називається невиродженою, якщо її визначник не дорівнює нулю, і виродженою, якщо дорівнює нулю.

Утворимо матрицю , елементами якої є алгебраїчні доповнення A_ij до відповідних елементів а_ij матриці, транспонованої до матриці А. Матрицю називають взаємною (приєднаною) для матриці А.

Якщо матриця А невироджена, то взаємна їй матриця А^* теж буде невиродженою, причому

Для довільної невиродженої матриці А існує тільки одна обернена матриця А^-1.