Уравнение состояния газа Ван - дер - Ваальса

Голландский физик Ван - дер – Ваальс в 1873 году предложил учитывать взаимодействие между молекулами и их размеры в виде поправок, вносимых в уравнение (1).

Поправка на внутреннее давление.

Необходимость такой поправки обусловлено тем, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания, так как молекулы представляют собой сложные пространственные структуры, содержащие как положительные, так и отрицательные заряды. Эти силы в теории идеального газа во внимание не принимаются. Силы взаимодействия между молекулами и атомами газа, не приводящие к образованию химических соединений, называют короткодействующими силами, так как они проявляются на расстояниях 10^-9 м, сравнимых с размерами молекул.

Зависимости результирующей силы F и потенциальной энергии E_p взаимодействия между молекулами от расстояния между их центрами представлены на рис. 2. При некотором расстоянии r = r₀ результирующая сила межмолекулярного взаимодействия обращается в нуль F=0. Это расстояние условно можно принять за диаметр молекулы d. Таким образом, расстояние r₀ соответствует равновесному состоянию между молекулами, на котором они находились бы в отсутствии теплового движения. При r < r₀ преобладают силы отталкивания (F_о > 0). При r > r₀ преобладают силы притяжения F_п < 0. Доказательством преобладания сил притяжения над силами отталкивания является слияние капелек жидкости. На расстоянии >10^-9 м межмолекулярные силы практически отсутствуют (рис. 2).

Рис. 2. Результирующая сила взаимодействия F и потенциальная энергия

взаимодействия E_p двух молекул. F > 0 –отталкивание, F < 0 –притяжение

Потенциальная энергия взаимодействия при r = r₀ минимальна. Чтобы удалить друг от друга две молекулы, находящиеся на расстоянии r₀, нужно сообщить им дополнительную энергию E₀. Величина E₀ называется глубиной потенциальной ямы или энергией связи молекулы.

Когда молекула газа летит к стенке сосуда, а затем отражается от нее, то изменяется ее импульс. Однако, в отличие от идеальных газов, импульс налетающих молекул изменяется не только под действием сил со стороны стенки, но и под действием сил, с которыми их тянут внутрь объема молекулы пристеночного слоя газа (в случае преобладания сил притяжения). В частности, под действием этих сил молекула может отразиться внутри пристеночного слоя, не долетев до стенки. Пусть Р давление стенки сосуда на газ (ее зафиксирует манометр), а Р_i – средняя сила, отнесенная к единице площади, с которой молекулы пристеночного слоя втягиваются внутрь газа. Тогда давление, под которым находится газ, будет больше, чем покажет манометр и определится суммой Р + Р_i.

Поправка на собственный объем молекул.

Так как молекулы газа имеют собственный объем, часть объема сосуда (а при высоких давлениях, она оказывается сопоставима с объемом сосуда) оказывается занятой ими. Свободный объем для молекул реального газа находят, вычитая из объема сосуда V «запрещенный» объем νb, обусловленный собственным объемом молекул (V–νb). Внесение Ван дер Вальсом поправок на внутреннее давление и собственный объем молекул в уравнение (1) привело к уравнению ,носящее его имя

(Р + Р_i ) (V –νb)= νRT ( 2)

где Р - давление, измеряемое манометром, V-объем сосуда, νb «запрещенный» объем, b- постоянная для данного газа, Т–абсолютная температура, ν-число молей, R- универсальная газовая постоянная.

Для изотермического процесса ( Т – постоянна ) νRT = Const. Используя выражение (2) получим для двух различных состояний (Р₀,V₀; Р,V ) газа уравнение:

(Р₀ + Р_i0 ) (V₀ –νb)= (Р + Р_i ) (V –νb). (3)

При комнатных давлении, объеме и температуре (начальные условия Р₀,V₀) внутреннее давление Р_i0 для газа, который будет изучаться, много меньше Р_i0 ‹‹ Р_{0 ,} а объем сосуда V » νb , тогда введенными поправками можно пренебречь. В результате из выражения (3) получим формулу для оценки внутреннего давления в виде.

(4)

Вычитаемое в формуле (4) можно получить из закона Бойля- Мариотта оно определяет собой давление Р_ид, т.е. давление идеального газа, давление, которое имел бы газ, если бы взаимодействие между молекулами и собственный объем молекул были пренебрежимо малы.

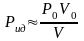(5)

СХЕМА ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Изучаемый газ (бутан С₄Н₁₀) заключен в стеклянной трубке 1 (рис. 3.) Давление в установке создается винтом с поршнем 5, который сжимает эластичный баллон, наполненный жидкостью 3. Жидкость поступает в стеклянную трубку и подобно поршню сжимает парогазовую среду. Она состоит из исследуемого газа и насыщенного пара жидкостного поршня. Внутреннее давление в трубке P, измеряемое манометром, складывается из парциального давления изучаемого газа P_г и давления насыщенного пара Р_п, определяемого температурой жидкости. Парциальное давление исследуемого газа будет равно

Р _г = Р - Р_{п .}. (6)

Рис. 3. Лабораторная установка по изучению реального газа:

1-прозрачная трубка с газом; 2 - жидкостный поршень; 3 - эластичный бал

лон, заполненный жидкостью;4- плунжер;5 - винт для сжатия;

6-манометр; 7-электронный термометр с термопарой;8- источник тока

нагревателя; 9- заглушка; 10 - конденсат

При комнатной температуре t = 24˚C P_п=0,03aт., при 50˚С P_n = 0,12 ат. Учитывая, что цена деления манометра 0,2ат поправку на P_п можно считать систематической ошибкой. Ей можно пренебречь, если не требуется высокая точность измерений.

Так как вся система газ-жидкость находится под атмосферным давлением Р_атм, то давление Р, которое испытывает исследуемый газ определим, пренебрегая вкладом P_н, по формуле

Р = Р_{атм .}+ Р_м (7)

Объем газовой фазы в установке определяется по высоте h газового столба известного и постоянного сечения S. Так как S- площадь сечения трубки (равна 7.1 мм²), а h-высота столба газа, то объем газа равен V = hS. На этом основании формулу ( 6 ) представим в виде

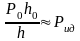(8)

Нагревание газа осуществляется путем пропускания тока по тонкой металлической ленте, наклеенной с боков трубки. Температура трубки (газа) измеряется электронным термометром с термопарой, спай которой вплотную прилегает к трубке.

Приборы. Технический барометр, цена деления 0,2 ат. (Одна техническая атмосфера 1 ат = 0,98·10⁵ Па ); миллиметровая линейка, цена деления 1 мм. Электронный термометр, цена деления 0,1 ⁰ С.