Контрольные вопросы

1. Что называется математическим и физическим маятниками?

1. При каких условиях колебания этих маятников являются гармоническими?

2. От каких параметров (величин) зависят циклическая частота  и период колебаний математического и физического маятников?

3. Как связан момент инерции I и период колебаний оборотного маятника от положения его грузов и призм?

4. С какой целью в работе перемещают призму оборотного маятника?

5. С какой целью строят график зависимости T = f(L) для оборотного маятника?

6. Почему период Т₁ мало изменяется при изменении положения призмы 9(2)?

ЛАБОРАТОРНАЯ РАБОТА № 1-5-4

Колебания связанных маятников

Цель работы: изучение основных закономерностей колебаний систем с несколькими степенями свободы на примере двух связанных маятников.

Постановка задачи

В природе и технике широко распространены колебательные системы, взаимодействующие между собой. К таким системам относятся ионы в кристаллической решетке, сложные молекулы, различные технические конструкции.

Простейшей системой с двумя степенями свободы в механике являются два маятника в виде стержня длиной L с грузами массой m (диск) на его концах. Маятники связаны невесомой пружиной с коэффициентом

ж

d

есткости k. Пружина находится на расстоянии d от точек подвеса, расположенных на горизонтальной прямой (рис. 1).

П

f_у

f_у

x₁

x₂

₂

L

ри движении маятников в одной вертикальной плоскости состояние такой системы полностью описывается двумя независимыми параметрами углами ₁ и ₂ отклонения маятников от вертикали, т.е. система имеет две степени свободы.

У

₁

V₂

V₁

равнение движения для каждого маятника можно получить из общего уравнения динамики вращательного движения стержня с грузом вокруг неподвижной оси

Рис. 1

. (1)

Здесь   угол поворота, M  момент действующих на тело сил относительно оси подвеса,   угловое ускорение, I  момент инерции каждого маятника относительно оси подвеса.

На каждый маятник действует сила тяжести mg, приложенная к ихцентру масс, и сила упругости f=-kx, где k  коэффициент жесткости пружины, x – ее деформация. Величина деформации x при малых ₁ и ₂, в соответствии с рис.1, находится как длина дуги, опирающейся на прямые d: x = d(₂  ₁). Следовательно, сила f = kd(₂  ₁).

Соответствующие этим силам вращающие моменты сил для малых углов колебаний имеют вид

M_тяж =  mgLSin   mgL, (2)

M_упр1 = kd(₂  ₁)d = kd²(₂  ₁) =  M_упр2.

Момент сил отрицателен, т.к. он возвращает маятник в положение равновесия. Уравнение (1) для каждого из маятников запишется:

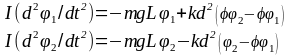(3)

М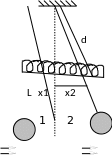 аятники могут длительное время колебаться, сохраняя, например, положение, изображенное на рис.1. В этом случае f_упр=kd(₂₁). Для рис. 2 f_упр = kd(₂+₁).

Введем новые переменные

₁ + ₂ = ₁ и ₂  ₁ = ₂, (4)

характеризующие относительное движение маятников. Просуммируем левые и правые части уравнений (3). Затем поделим результирующее уравнение на I. С учетом новых переменных получим

. (5)

И

Рис. 2

з второго уравнения системы (3) вычтем первое. В итоге получим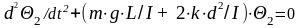

(6)

Каждое из уравнений (5) и (6) аналогично дифференциальному уравнению для гармонических колебаний (см. лаб. раб. № 1-5-1) вида

.

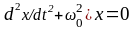При сопоставлении получаем, что собственные частоты колебаний равны

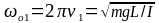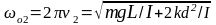; (7)

Момент инерции маятника складывается из момента инерции стержня массой m_ст и длиной L₀(I_ст = m_стL₀²/3), момента инерции диска радиусом R и массой m, удаленного на расстояние L от точки подвеса

I = m_стL₀²/3 + mL² + mR²/2. (8)

Решения уравнений (5) и (6), как известно, имеют вид

₁ = Аcos(_o1t + ₁), ₂ = Bcos(_o2t + ₂), (9)

где A и B – амплитуды изменений величин ₁ и ₂ , а ₁ и ₂  соответственно их начальные фазы.

Из (9) и (4) находим закон изменения угла  для каждого маятника:

₁ = 1/2(₁  ₂) = A/2cos(_o1t + ₁)  B/2cos(_o2t + ₂) (10)

₂ = 1/2(₁ + ₂)= A/2cos(_o1t + ₁) + B/2cos(_o2t + ₂)

Из (10) видно, что колебания каждого маятника складываются из двух независимых колебаний с частотами _o1 и _o2, определяемых выражениями (7), которые носят название нормальных частот или мод, при этом, как видно из (7), _o2 > _o1. Если обратиться к уравнениям (7) ,то в первом из них выражена собственная частота свободных незатухающих колебаний физического маятника 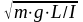. Когда упругая связь не действует, т. е. ₂  ₁ = 0, маятники движутся синхронно в одном направлении параллельно друг другу (синфазно).

Во втором уравнении частота _o2 > _o1 за счет действия упругой связи, которая будет максимальна, если маятники движутся точно в противофазе навстречу друг другу или друг от друга (рис. 2).

При любом другом движении осуществляются колебания с частотой _k, лежащей в диапазоне от _o1 до _o2. Если вклад сил упругости в изменение частоты невелик, т.е. 2kd²/I < mgL/I, то частоты _o1 и _o2 близки и результат сложения колебаний представляется в виде биений. При этом амплитуда медленно изменяется с частотой биений:

_б = _o2  _o1 или _б = ₂  ₁. (11)

Если с помощью внешней периодической силы, частота которой будет возрастать от нуля, действовать на связанную колебательную систему, то при частотах вынуждающей силы , близких к ₁ и ₂, будет наблюдаться два резонанса, т.е. резкое увеличение амплитуды колебаний маятников. Зависимость A= f() будет иметь два максимума.