Графики

Графики обычно используют, когда требуется определить характер поведения какой-либо функции или процесса. Excel позволяет строить 7 типов графиков, разбитых на 3 категории: график, график с маркерами и объемный график.

Для примера рассмотрим построение графика функции y = sin(x) на интервале одного полного периода. Для этого нужно построить таблицу, содержащую столбец аргументов и столбец значений функции (рис. 11).

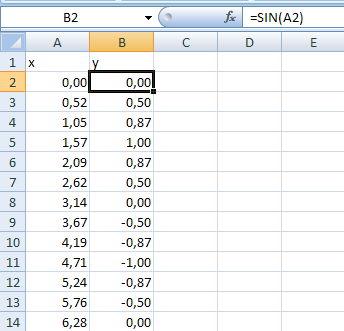
Рис.11. Исходные данные для построения графика функции y = sin(x)

Для построения графика по заданным точкам необходимо выделить столбец таблицы, по которым должен быть построен график. Желательно включение в выделенный фрагмент строки с названием рядов.

После указания исходных данных необходимо перейти на вкладку Вставка и выбрать тип будущего изображения (рис. 12). В группе команд График воспользоваться командой График График с маркерами.

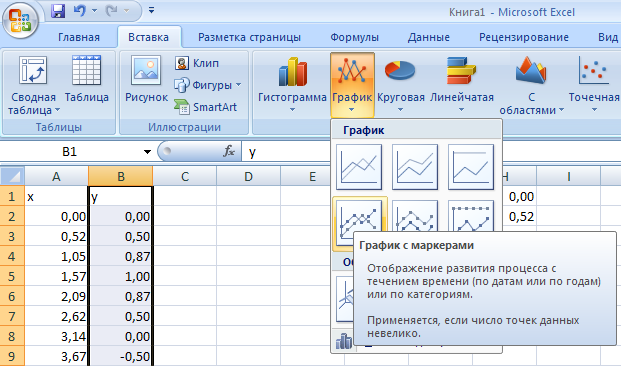
Рис.13. Выбор изображения

После построения графика по заданным точкам без использования сглаживания будет получена некоторая ломаная (рис.14).

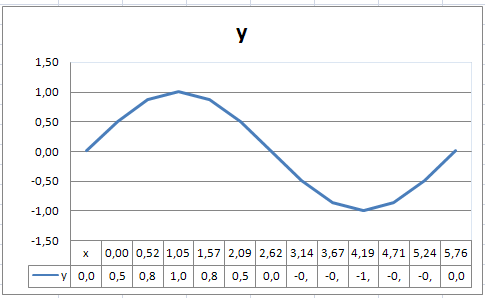
Рис.14. График функции y = sin(x) без сглаживания

Для того чтобы Microsoft Excel 2007 отобразил на экране плавную линию, следует включить режим сглаживания. Для этого следует выделить построенный график и вызвать команду Формат ряда данных контекстного меню. В открывшемся окне на вкладке Тип линии следует выбрать опцию сглаженная линия и нажать клавишу Закрыть. В результате график функции синуса примет вид, представленный на рис.15.

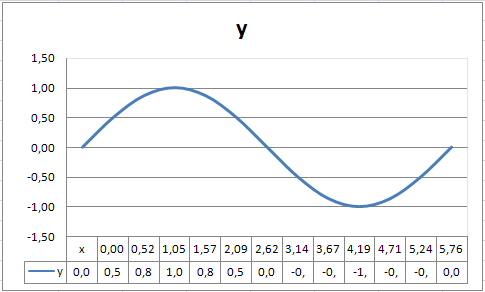
Рис. 15. График функции y = sin(x) со сглаживанием

Задания к лабораторной работе Построение двумерных графиков в Excel 2007

1. Построить следующие графики функций: y = f(x), z = f(x); нанести сетку, легенду, название графика и осей координат (варианты заданий приведены в табл. 1);

2. По графику сделать вывод о наличии экстремума (минимума или максимума) исследуемой функции.

Таблица 1

№	Функции и	Диапазон и шаг изменения аргумента
1	;	,
2	;	,
3	;	,
4	;	,
5	;	,
6	;	,
7	;	,
8	;	,
9	;	,
10	;	,
11	;	,
12	;	,
13	;	,
14	;	,
15	;	,
16	;	,
17	;	,
18	;	,