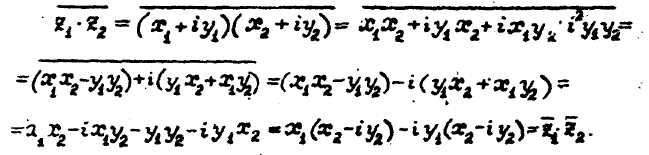- •Математический анализ.
- •1.Множества.
- •1) Множество, его характеристическое свойство. Способы задания. Привести примеры.
- •2) Множества: конечные, бесконечные. Отношения включения, универсальное множество. Диаграмма Эйлера-Венна. Привести примеры.
- •2.Общие свойства функций.
- •13) Обратная функция. Необходимое и достаточное условие обратимости. Доказать признак обратимости функции.
- •14) Доказать теорему о графиках взаимно-обратных функций. Отыскание обратных для алгебраических и трансцендентных. Привести примеры.
- •15) Чётные и нечётные функции. Доказать теоремы об их графиках. Доказать арифметические теоремы об указанных функциях. Привести примеры.
- •17) Периодические функции. Доказать арифметические теоремы о периодических функциях. Доказать теорему о периодичности сложной функции от периодической функции. Привести примеры.
- •3.Числовые последовательности и пределы.
- •4.Предел функции.
- •31) Бесконечно малая функция. Доказать теорему о функции, её пределе и бесконечно малой функции.
- •32) Доказать арифметические теоремы о пределах функций:
- •33) Доказать теорему о связи бесконечно большой и бесконечно малой функций.
- •34) Односторонние пределы. Доказать теорему о связи существования предела функции в точке с существованием односторонних пределов функции.
- •35) Доказать теоремы о единственности предела в точке и о предельном переходе в равенстве двух функций.
- •5.Непрерывность функции в точке.
- •6.Производная функции в точке.
- •7.Основные теоремы дифференциального исчисления.
- •56) Доказать теорему Роля и теорему Лагранжа о конечном приращении функции. Рассказать о геометрической интерпретации этих теорем.
- •Алгебра.
- •8.Линейная функция.
- •9.Квадратный трёхчлен.
- •10.Комплексные числа.
- •62) Комплексная плоскость. Действия над комплексными числами в декартовой форме.
- •68) Комплексно-сопряжённые числа. Теоремы о сопряжённости суммы и произведения комплексно-сопряжённых чисел.
- •11.Теория многочленов.
- •69) Действия над многочленами. График многочлена. Алгоритм деления многочленов с остатком (алгоритм Евклида).
- •70) Теорема Безу. Следствия.
- •12.Дробно-рациональная функция.
- •76) Правильная и простейшие рациональные дроби. Теорема о представлении рациональной дроби в виде суммы многочлена и правильной дроби. Алгоритм разложения правильной дроби в сумму простейших дробей.
- •13.Степенная и показательная функция.
- •14.Логарифм числа и логарифмическа функция.
- •15.Тригонометрические функции.
- •Стереометрия.
- •16.Аксиоматика Вейля-Рашевского.
- •102) Аксиоматический метод. Независимость, полнота и непротиворечивость системы аксиом.
- •109) Понятие направления. Отношения сонаправленности, противонаправленности и коллинеарности векторов.
- •110) Аксиомы размерности. Два определения линейной зависимости (независимости) векторов. Доказать их эквивалентность.
- •111) Доказать теорему о системе векторов, содержащей линейно зависимую подсистему. Следствия.
- •112) Доказать теорему о подсистеме линейно независимой системы векторов.
- •17.Аффинное пространство.
- •113) Аффинное пространство. Базис. Размерность. Привести примеры аффинных пространств различной размерности.
- •114) Доказать теорему о существовании и единственности разложения вектора по произвольному базису. Координаты векторов.
- •115) Аффинная система координат. Радиус-вектор. Координаты точки. Доказать теорему о координатах векторов.
- •116) Доказать теорему о координатах суммы векторов.
- •117) Аффинное пространство. Доказать теорему о координатах вектора, умноженного на число.
- •18.Метрнческое пространство
- •151) Векторное произведение и коллинеарности векторов. Правые (левые) тройки векторов в декартовой системе.
- •152) Смешанное произведение векторов. Доказать свойства смешанного произведения. Смешанное произведение векторов в декартовой системе координат. Доказать признак компланарности векторов.
- •153) Расстояние между геометрическими фигурами. Вывести формулу дли вычисления расстояния от точки до плоскости.
- •154) Вывести формулу для вычисления расстояния между скрещивающимися прямыми.
Алгебра.
8.Линейная функция.
62) Доказать свойства линейной функции и построить её график. Привести примеры. Вывести уравнение прямой, проходящей через две заданные точки.
Коэффициент k обозначает тангенс угла наклона, а свободный коэффициент точка пересечения с осью оу.
(x-xa)\(xb-xa)=(y-ya)\(yb-ya)(выводится через систему)
63) Доказать условие параллельности и перпендикулярности прямых. Вывести формулу для тангенса угла между прямыми.
k1=k2 – прямые параллельны.
k1k2=-1 – прямые перпендикулярны
tgφ=| (k1-k2)\ (1+k1k2)|
9.Квадратный трёхчлен.
59) Выделение полного квадрата. Привести примеры. Вывести формулы для его корней. Дискриминант. Доказать прямую и обратную теоремы Виета.
Выделение полного квадрата:
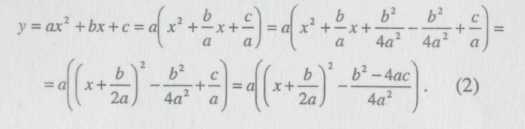
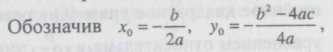 и
получим канонический вид квадратного
трёхчлена.
и
получим канонический вид квадратного
трёхчлена.
Формулы его корней:
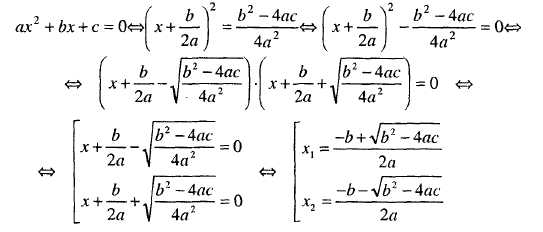
Выражение вида b2-4ac принято называть дискриминантом.
Прямая теорема Виета:

Обратная теорема Виета:

60) Доказать теорему о разложении на линейные множители квадратного трёхчлена. Построение графика квадратного трёхчлена по его коэффициентам.
Если х1 и х2 – корни квадратного уравнения, то квадратный трёхчлен разлагается на линейные множители вида: Ax2+Bx+C=A(x-x1)(x-x2)
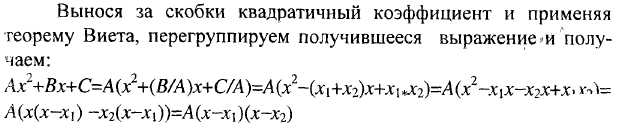
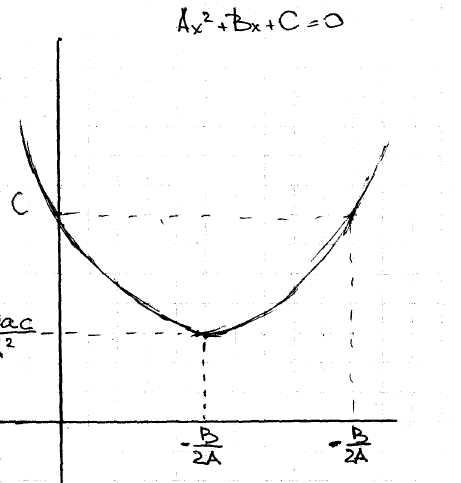
61) Доказать необходимое и достаточное условие того, что данное число меньше корней квадратного уравнения.
- Доказать необходимое и достаточное условие того, что данное число располагается между корнями квадратного уравнения.
- Доказать необходимое и достаточное условие того, что данное число больше корней квадратного уравнения.
- Доказать необходимое и достаточное условие того, что данное число совпадает с меньшим (большим) корнем квадратного уравнения.
f()\А<0
система: f()\А>0; хв->0 (больше)
система: f()\А>0; хв-<0 (меньше)
система: f()\А=0; хв->0 (совпадает с большим)
система: f()\А=0; хв-<0 (совпадает с меньшим)
Доказывается банально через рисунки (4 параболы). И ко всем условиям надо не забывать дискриминант больше либо равен нуля.
10.Комплексные числа.
62) Комплексная плоскость. Действия над комплексными числами в декартовой форме.
С помощью базисных векторов задаются целая и мнимая части комплексного числа.
Суммой двух комплексных чисел z1 и z2 называют комплексное число z=(x1+x2)+i(y1+y2). Другими словами для нахождения суммы двух комплексных чисел необходимо сложить их действительные и мнимые части. Сумма двух комплексно-сопряжённых чисел есть всегда действительное число равное их удвоенной действительной части.
![]()
Для нахождения разности комплексных чисел необходимо вычесть отдельно их действительные и мнимые части.
Произведением двух комплексных чисел z1 и z2 называют комплексное число
![]()
68) Комплексно-сопряжённые числа. Теоремы о сопряжённости суммы и произведения комплексно-сопряжённых чисел.
Два комплексных числа называют комплексно сопряженными, если они имеют одну и ту же действительную часть и взаимно противоположные мнимые части.
Число, сопряжённое с суммой комплексных чисел есть сумма чисел сопряжённых слагаемым.
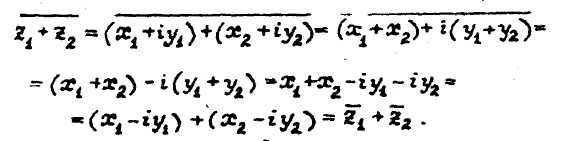
Число, сопряжённое с произведением двух комплексных чисел есть произведение чисел, сопряжённых с сомножителями.