17) Периодические функции. Доказать арифметические теоремы о периодических функциях. Доказать теорему о периодичности сложной функции от периодической функции. Привести примеры.

Функция f(x) называется периодической с периодом Т, если выполняется равенство f(x-t)=f(x+t).

Если функции f(x) и g(x) периодические с периодами Т и Р соответственно, то периодом алгебраической суммы, разности, произведения и частного этих функций является общим кратным периодов Т и Р. (Доказывается банальной подстановкой, учитывая, что каждый период функции кратен её основному).

Периодом сложной функции от периодической является период функции-аргумента. (Доказывается подстановкой).

3.Числовые последовательности и пределы.

18) Модуль числа. Доказать неравенство о модуле суммы. Доказать неравенство о модуле разности. Доказать теорему о модуле произведения и частного двух чисел.

Модулем числа х называется такое число, которое равно х, если х больше или равно нуля, и равно –х, если х меньше нуля.

|

<= Доказывается это всё перебором

x|+|y||x+y|

|x|-|y||x+y|

|xy|=|x||y|

|1\x|=1\|x|

19) Арифметическая прогрессия, свойства. Вывести формулу общего члена и суммы первых n-членов прогрессии.

Арифметическая прогрессия – это такая числовая последовательность, для каждого члена которой справедливо равенство: a_n=a_n-1+d, где d это разность.

Любой элемент прогрессии равен среднему арифметическому двух своих равноудалённых соседей.

20) Геометрическая прогрессия, свойства. Вывести формулу общего члена и суммы первых n-членов прогрессии.

Геометрическая прогрессия – это такая числовая последовательность, для каждого члена которой справедливо равенство: a_n=a_n-1*q, где q это знаменатель.

Любой элемент прогрессии равен среднему геометрическому двух своих равноудалённых соседей.

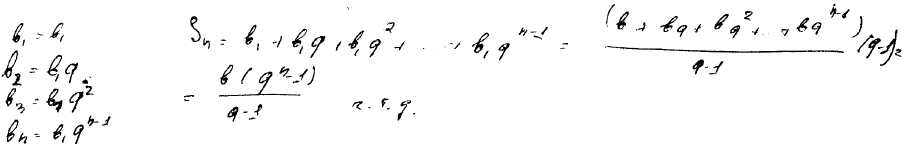
21) Предел бесконечной последовательности, геометрическая интерпретация. Доказать теорему о единственности предела последовательности.

Lim x_n=a, если для любого >0 существует такое N₀ и зависящего от , такое что для любого n N₀ выполняется равенство |x_n-a|< 

Геометрический смысл это -окружность вне которой находится конечное число элементов последовательности.

Последовательность не может иметь более одного предела. (Доказывается от противного, предположим, что 2 предела существуют и их -окружности не пересекаются – далее противоречие определению).

22) Бесконечно малая последовательность. Доказать теорему о последовательности, её пределе и бесконечно малой последовательности. Доказать теорему о произведении бесконечно малой последовательности на ограниченную последовательность.

Последовательность a_n называется бесконечно малой, если её предел равен нулю.

Для того что бы число а являлось пределом последовательности a_n необходимо и достаточно чтобы последовательность {a_n-a} была бесконечно малой.

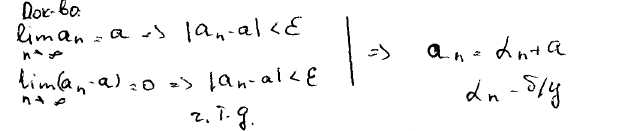
Произведение ограниченной и бесконечно малой последовательностей, так же является бесконечно малой последовательностью.

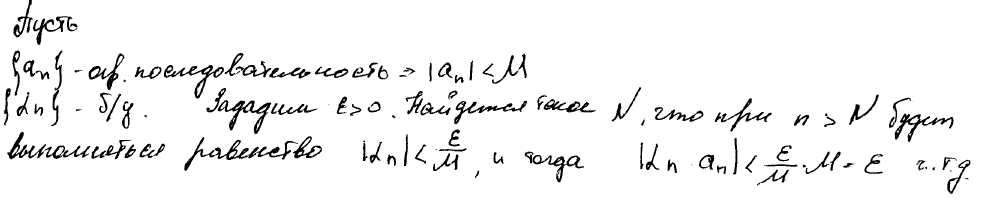
23) Доказать арифметические теоремы о пределах сходящихся последовательностей:

-о пределе суммы двух сходящихся последовательностей

-о пределе произведения двух сходящихся последовательностей

-о пределе отношения двух сходящихся последовательностей

Предел суммы равен сумме пределов.

Предел произведения равен произведению пределов.

Предел отношения равен отношению пределов.

24) Бесконечно большая последовательность. Доказать теорему о связи бесконечно малой и бесконечно большой последовательностей.

Последовательность a_n называется бесконечно большой, если для любого числа А найдётся такое N, что для любого n>N будет выполняться неравенство |a_n|<A.

Если последовательность а_n является бесконечно большой, то последовательность 1/a_n является бесконечно малой.

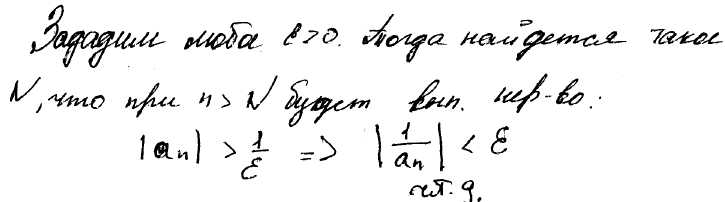
25) Доказать теорему о переходе к пределу в неравенстве для двух последовательностей.

Если для всех значений N, кроме, может быть, конечного числа, выполняется неравенство a_n<b_n, при этом пределы этих последовательностей равны a и b соответственно, то a<b.

26) Доказать теорему о «зажатой» последовательности.

Если даны три последовательности a_n, b_n и c_n причём lim a_n=lim c_n=b и для всх n выполняется неравенство a_nb_nc_n то и последовательность b_n тоже имеет предел, равный b.

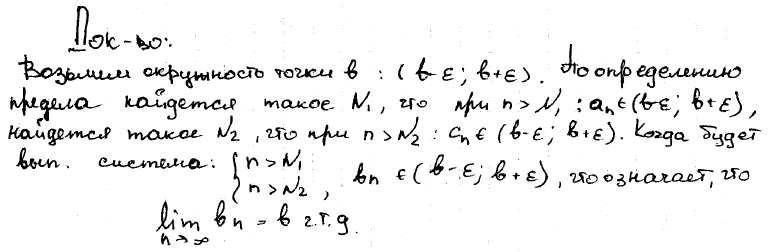
27) Необходимое и достаточное условие существования предела последовательности.

Ограниченность и монотонность.

28) Доказать второй замечательный предел для последовательности.

29) Вывести формулу сумм членов бесконечно убывающей геометрической прогрессии.