18.Метрнческое пространство

134) Аксиомы скалярного произведения. Длина вектора. Орты. Доказать теорему о нормировании вектора.

АКС.1: Для любых двух векторов существует действительное число, называемое их скалярным произведением (а,b).

АКС.2: Скалярное произведение обладает свойством коммутативности.

АКС.3: Числовой множитель можно выносить за скобки скалярного произведения.

АКС.4: Скалярное произведение дистрибутивно относительно сложения векторов.

АКС.5: скалярный квадрат вектора неотрицателен.

Длиной вектора называется корень из скалярного квадрата этого вектора.

Вектор называется ортом , если его длина равна 1.

Для любого вектора существует вектор коллинеарный ему, длина которого равна 1.

135) Доказать неравенство Коши-Буняковского.

Модуль скалярного произведения векторов не превосходит произведения длин этих векторов.

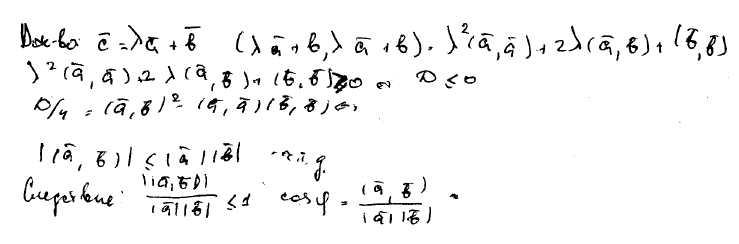
136) Угол между векторами и расстояние между точками. Доказать свойства расстояния.

Косинус угла между векторами равен скалярному произведению, деленному на произведение моделей векторов.

Расстоянием называется величина вектора, соединяющего эти точки.

Свойства расстояния: 1) оно не отрицательно;

2) расстояние от А до В равно расстоянию В до А;

3) неравенство треугольника;

137) Ортогональность системы векторов. Доказать существование двух (трёх) ненулевых ортогональных векторов.

Ортогональные системы ненулевых векторов линейно независимы. (Доказывается записью 2-х скалярок, где один вектор представлен в виде линейной комбинации двух других.)

Существует 3 (2) ненулевых вектора.

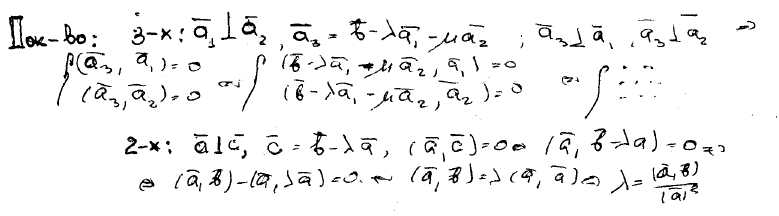
138) Доказать линейную независимость ортогональной системы векторов.

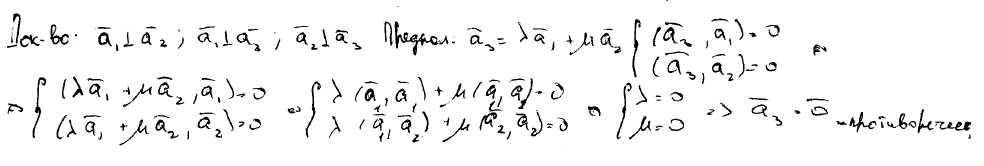
139) Проекция вектора на вектор.

Проекцией вектора а на вектор b называется скалярное произведение векторов а и b, деленное на модель вектора b.

140) Доказать теорему о проекции произведения вектора на число. Доказать теорему о проекции вектора на ось.

Т: Проекция произведения вектора на число равна произведению проекции этого вектора на число.(Выводится через определение)

Т: Проекция вектора на ось равна координатам вектора. (Выводится через определение)

141) Доказать, что в декартовой системе координаты вектора есть его проекции на оси координат.

Доказывается по определению.

142) Декартова система координат. Доказать теорему о скалярном произведении.

Декартовой системой координат называется аффинная система координат с ортонормированным базисом.

В декартовой системе координат скалярное произведение двух векторов равно сумме по парных произведений их координат.

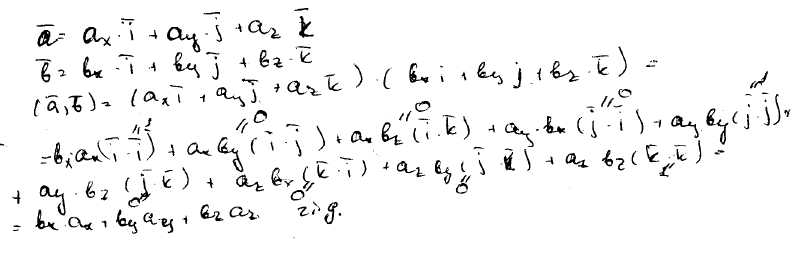
143) Доказать теоремы о длине вектора, расстоянии между точками и угле между векторами.

Т: В декартовой системе координат длина вектора равна квадратному корню из суммы квадратов координат.

Сл.: Расстояние между точками А и В равно квадратному корню из суммы квадратов разностей соответствующих координат (причём из координат 2-й точки вычитаются координаты 1-й).

Формула для вычисления косинуса угла та же.

144) Признак перпендикулярности прямой и плоскости.

О: Прямую, пересекающую плоскость, называют перпендикулярной этой плоскости, если она перпендикулярна ко всем прямым принадлежащим этой плоскости.

Т: Что бы прямая была перпендикулярна плоскости, необходимо и достаточно, что бы она была перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

145) Теорема о плоскости, проходящей через прямую перпендикулярную другой плоскости и обратная теорема.

Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой.

146) Теорема о параллельной проекции прямой.

Прямая проектируется в прямую или точку.

147) Теорема о проекциях параллельных прямых.

Параллельные прямые проектируются либо в две параллельные прямые, лиюо в одну и туже прямую.

148) Теорема о трёх перпендикулярах.

Для того, чтобы прямая l, принадлежащая плоскости , была перпендикулярна наклонной, проведенной к этой плоскости, необходимо и достаточно, чтобы та прямая была перпендикулярна проекции наклонной на ту же плоскость.

149) Двугранные углы. Теорема о площади проекции многоугольника.

Это углы образованные двумя плоскостями.

Площадь ортогональной проекции многоугольника равна площади самого многоугольника на косинус угла между многоугольником и его проекцией.

150) Векторное произведение векторов. Доказать свойства векторного произведения.

О: Векторным произведение 2-х векторов а и b называется вектор, перпендикулярный векторам а и b, образующий с векторами а и b правый базис и равный по модулю произведению длин векторов а и b на синус угла между ними. (аb)

Св-ва: 1) (а0)=0

2) |(ab)|=площади параллелограмма, построенного на этих векторах.

3) (ba)=-(ab)

4) Числовой множитель можно вынести за знак векторного произведения: (ab)=(ab)

5) ((a+b) c)=(ac)+(bc)

i j k x1 y1 z1 x2 y2 z2

6) (ab)=

символический

определитель.