3. Марковський процес з неперервним часом та дискретними станами

Якщо заданий марковський процес зі скінченною кількістю станів , ,…, і неперервним часом, то для знаходження ймовірностей , , …, складають систему лінійних диференціальних рівнянь. Нехай − інтенсивність переходу системи зі стану у стан . Для кожного складаємо диференціальне рівняння

.

До цієї системи додають ще рівняння

+ + …+ =1.

Якщо в початковий момент система знаходиться в стані , то до даної системи диференціальних рівнянь долучають ще початкові умови :

, ,.., ,…, .

Щоб знайти граничний режим, тобто випадковий процес, який встановиться в системі при , у заданій вище системі лінійних диференціальних рівнянь покладають . Разом з рівнянням + + …+ =1 ми будемо мати систему лінійних алгебраїчних рівнянь, з якої знаходяться числа , , …, .

Зокрема, для системи з трьома станами отримаємо систему диференціальних рівнянь

. (3.1)

Приклад 8. Задано марковський процес з неперервним часом, трьома станами , , та інтенсивностями переходу , , , , , між цими станами. Знайти ймовірності , , перебування системи відповідно в станах , , у момент часу та граничний стан системи, якщо відомо, що в початковий момент часу система перебувала у стані .

Розв’язання. Запишемо систему (3.1) для даної задачі. Оскільки перші три рівняння цієї системи є лінійно залежними, то ми залишимо лише перші два з них

.

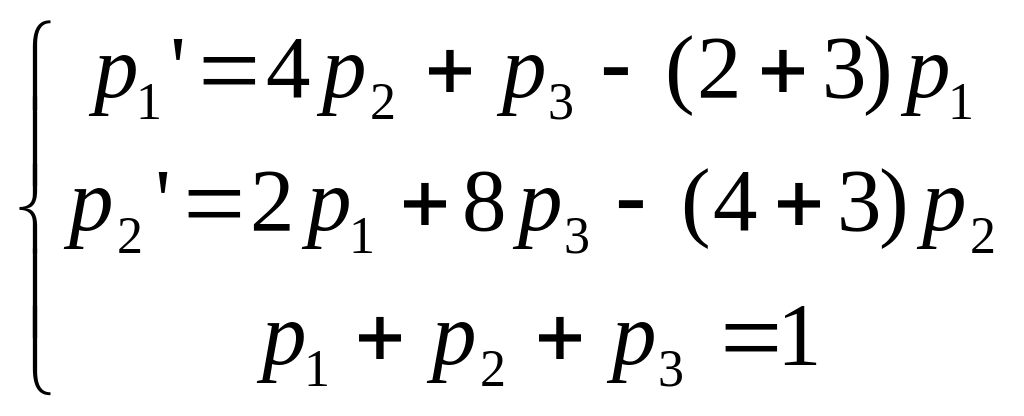Виразимо з третього рівняння та підставимо цей вираз у перші два рівняння:

.

З першого рівняння отримаємо . Продиференціювавши цю рівність будемо мати, що . Підставивши дані вирази у друге рівняння та звівши подібні доданки, отримаємо лінійне неоднорідне диференціальне рівняння зі сталими коефіцієнтами .

Щоб розв’язати відповідне однорідне рівняння

складемо характеристичне рівняння

.

Коренями цього рівняння будуть числа , . Таким чином, загальний розв’язок однорідного рівняння запишеться у вигляді . Частковий розв’язок неоднорідного рівняння відшукаємо методом підбору у вигляді функції . Тоді , звідки .

Отже, .

Тоді і

.

.

Підставляючи початкові умови , , отримаємо, що , .

Таким чином,

.

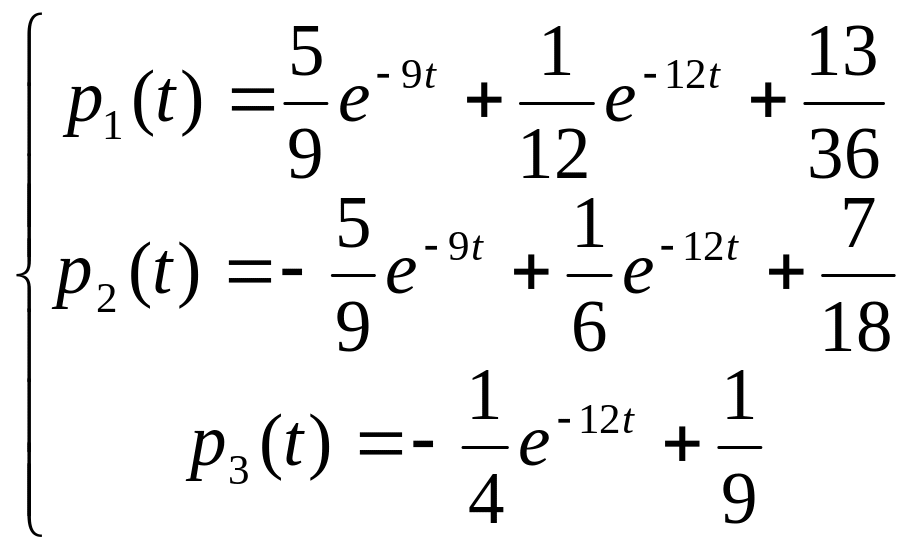Знайдемо граничний стан системи

;

;

.

4. Потоки

Послідовність подій, що відбуваються одна за одною називається потоком подій. Стаціонарним потоком називається потік для якого ймовірність появи подій за проміжок часу залежить лише від величини і не залежить від величини . Потоком без наслідків називається потік в якому кількості подій, що відбулися за проміжки часу, які не перетинаються, є незалежними випадковими подіями. Регулярним потоком називається потік подій, у якому події відбуваються одна за одною через строго визначені проміжки часу. Ординарним називається потік, для якого ймовірність появи більше ніж однієї події за нескінченно малий проміжок часу є нескінченно малою величиною більш високого порядку ніж ймовірність появи рівно однієї події за той самий проміжок часу. Розгалуженим називають потік розмноження і перетворення частинок в якому вони розвиваються незалежно одна від одної.

Нехай − математичне сподівання кількості подій, що відбудуться за проміжок часу .

Інтенсивністю потоку називається границя відношення середнього числа умов, що надійшли за час , до всього проміжку , коли :

.

Якщо відома інтенсивність потоку , то математичне сподівання кількості подій, що надійшли за проміжок часу можна обчислити за формулою

.

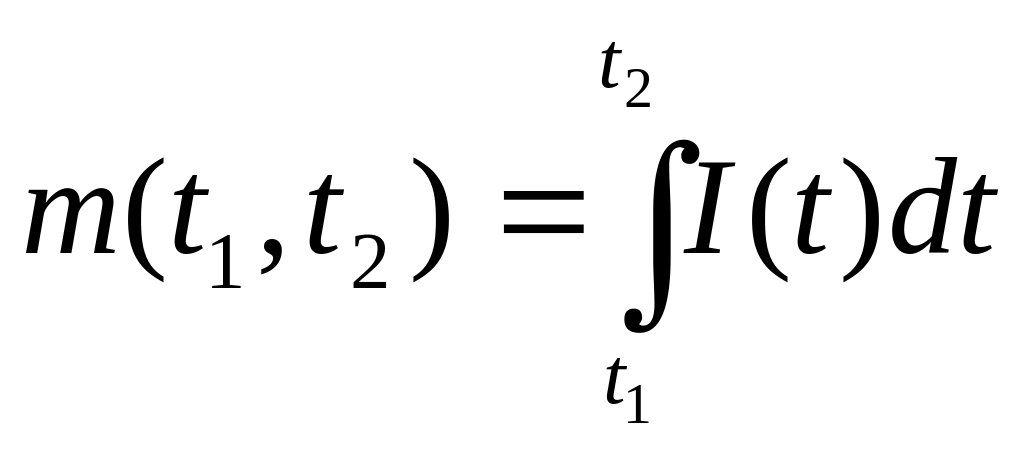Найпростіший, або пуассонівський потік – це потік, що задовольняє умови стаціонарності і відсутності наслідків.

Якщо маємо заданий пуассонівський потік, то ймовірність появи випадкової події раз протягом проміжку часу обчислюється за формулою

,

де − інтенсивність потоку.

Зокрема, ймовірність того, що за час жодна подія не настане, запишеться у вигляді

,

а ймовірність настання рівно однієї події за час буде рівна

.

Використовуючи формулу для ймовірності протилежної події, отримаємо, що ймовірність настання не більше ніж ніж однієї події за час буде рівна

.

Потоком Пальма називають потік подій для якого проміжки часу між сусідніми подіями є незалежними випадковими величинами. Якщо, крім того, ці випадкові величини є однаково розподіленими то потік Пальма називається стаціонарним.

Потоком Ерланга -ого порядку називається потік, який отримується із найпростішого шляхом “проріджування”: із найпростішого потоку викидають подій, що йдуть почергово, а залишають +1-у подію.

Приклад 9. На телефонну станцію надходить пуассонівський потік викликів інтенсивністю (викликів за хвилину). Знайти ймовірність того, що протягом 8 хвилин на телефонну станцію

1. не надійде жодного виклику;

2. надійде рівно два виклики;

3. надійде більше двох викликів.

Знайти математичне сподівання, дисперсію, середньо квадратичне відхилення кількості викликів, що надійдуть за цей період на телефонну станцію.

Розв’язання

1. .

2.

3.

Математичне сподівання .

Дисперсія .

Середньоквадратичне відхилення .

Приклад 10. Довести, що сума двох найпростіших процесів, з інтенсивностями та є найпростішим потоком та знайти його інтенсивність.

Розв’язання. За формулою повної ймовірності

.

Таким чином, сумарний потік є найпростішим потоком з інтенсивністю .