Міністерство освіти і науки, молоді та спорту України

Українська академія друкарства

Кафедра математики і фізики

Теорія випадкових процесів Методичні вказівки до розв’язування задач для студентів інженерних спеціальностей

Львів, ­2012

Пирч Н. М. Теорія випадкових процесів: методичні вказівки до розв’язування задач для студ. інженерних / Н. М. Пирч. ─ Львів : Українська академія друкарства, 2012. ─ 48 с.

Затверджено кафедрою математики і фізики Української академії друкарства (протокол № 1 від 14 червня 2012 року).

Автор:

Пирч Н. М., канд. фіз.-мат. наук, доцент

Автор висловлює щиру подяку Петрові Степановичу Сеньо за допомогу та цінні поради, висловлені при написанні даної роботи

Відповідальний за випуск:

Кульчицький А. Д., канд. фіз-мат. наук, доцент

Верстання:

Шевчук Г. Я.

Зміст

1. Випадковий процес та його характеристики………………….4

2. Марковський процес з дискретним часом та дискретними станами……………………………………………………………………14

3. Марковський процес з неперервним часом та дискретними станами..……………………………………………………………….19

4. Потоки……………………………………………………………….23

5. Системи масового обслуговування……………………………...27

6. Стаціонарні випадкові процеси………………………………….33

Вправи………………………………………………………………….39

Використана та рекомендована література……………………….49

Найвище призначення математики

полягає в тому, щоб знаходити

прихований порядок в хаосі, що оточує нас

Норберт Вінер

1. Випадковий процес та його характеристики

Випадковим процесом називається функція , значення якої при кожному фіксованому значенні є випадковою величиною. Випадкову величину , в яку реалізується випадковий процес при кожному конкретному значенні , називають перерізом цього процесу. Кожна конкретна функція, яку отримуємо при одному спостереженні випадкового процесу , називається реалізацією випадкового процесу . Випадковий процес називається процесом із дискретним часом, якщо система, в якій він перебуває може змінювати свої стани лише у фіксовані моменти часу , , …, , кількість яких скінченна або зліченна. У проміжках часу між інтервалами випадковий процес не змінює свого стану. Випадковий процес називається процесом із неперервним часом, якщо переходи системи із одного стану в інший можуть здійснюватися в будь-які випадкові моменти часу, що неперервно заповнюють цілий інтервал. Випадковий процес називається процесом із дискретними станами, якщо в будь-який момент часу перерізом його є дискретна випадкова величина. Випадковий процес називається процесом із неперервними станами, якщо в будь-який момент часу перерізом цього процесу є неперервна випадкова величина.

Для випадкового процесу функція

називається одновимірним законом розподілу або одновимірною функцією розподілу випадкового процесу . Для випадкового процесу із неперервними станами функція

називається одновимірною щільністю випадкового процесу . Для функції та є відповідно функцією розподілу та щільністю випадкової величини, що є перерізом випадкового процесу при .

Математичним сподіванням випадкового процесу називається невипадкова функція , яка при кожному значенні є математичним сподіванням відповідного перерізу. Зокрема для неперервних випадкових процесів має місце формула

.

Різницю називають флуктуаційною складовою випадкового процесу , або центрованим випадковим процесом, що відповідає процесу .

Дисперсією випадкового процесу називається невипадкова функція , яка при кожному значенні є дисперсією відповідного перерізу. Зокрема, для неперервних випадкових процесів має місце формула

.

Середнім квадратичним відхиленням випадкового процесу називається функція

.

Кореляційною функцією випадкового процесу називається функція

.

Для довільного має місце рівність .

Нехай − випадковий процес, − невипадкова функція. Розглянемо випадкові процеси , .

Тоді мають місце рівності

,

, .

Нормованою кореляційною функцією випадкового процесу називається функція

.

Розглянемо випадковий процес , всі можливі реалізації якого є диференційованими функціями. Тоді похідна випадкового процесу

є випадковим процесом, реалізації якого – це похідні реалізацій випадкового процесу . При цьому справедливими будуть рівності

, .

Нехай − неперервний випадковий процес, тоді

є також випадковим процесом. При цьому справедливими будуть наступні рівності

.

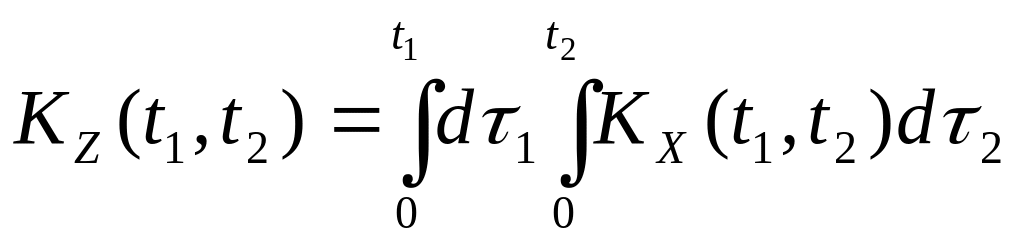Приклад 1. Для випадкового процесу , де − випадкова величина, що має нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням знайти

1. одновимірну функцію розподілу ;

2. одновимірну щільність розподілу ;

3. математичне сподівання ;

4. дисперсію ;

5. середнє квадратичне відхилення ;

6. флуктуаційну складову ;

7. кореляційну функцію ;

8. нормовану кореляційну функцію ;

9. записати випадковий процес ;

10. записати випадковий процес .

Розв’язання

1.

.

Якщо випадкова величина має нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням , то випадкова величина матиме нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням . Нехай − функція розподілу нормально розподіленої випадкової величини з математичним сподіванням і середнім квадратичним відхиленням . Тоді

.

2. Нехай − щільність розподілу нормально розподіленої випадкової величини з математичним сподіванням і середнім квадратичним відхиленням .

Тоді

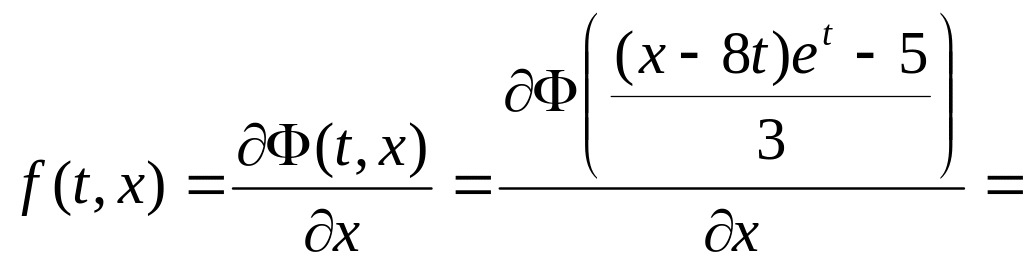
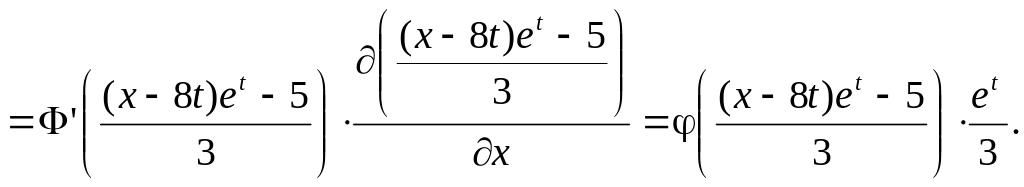
3. Нагадаємо, що математичне сподівання від суми двох випадкових процесів дорівнює сумі математичних сподівань процесів-доданків, невипадкову функцію можна виносити перед знак математичного сподівання, математичне сподівання від невипадкової функції дорівнює цій функції. Тому,

4. Нагадаємо, що додавання до випадкового процесу невипадкової функції не змінює його дисперсії. Невипадкову функцію можна, піднісши її до квадрату, винести перед знак дисперсії. Тому,

.

5. .

6. Флуктуаційна складова випадкового процесу буде рівна

.

7.

.

8. .

9. .

10.

Приклад 2. Задано математичне сподівання та кореляційна функція випадкового процесу . Знайти математичне сподівання, кореляційну функцію та дисперсію випадкового процесу .

Розв’язання.

Знайдемо кореляційну функцію:

.

Дисперсія: .

Приклад 3. Задано математичне сподівання та кореляційну функцію випадкового процесу . Знайти математичне сподівання, кореляційну функцію та дисперсію випадкового процесу .

Розв’язання. .

.

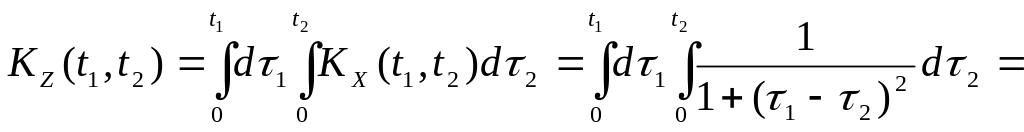
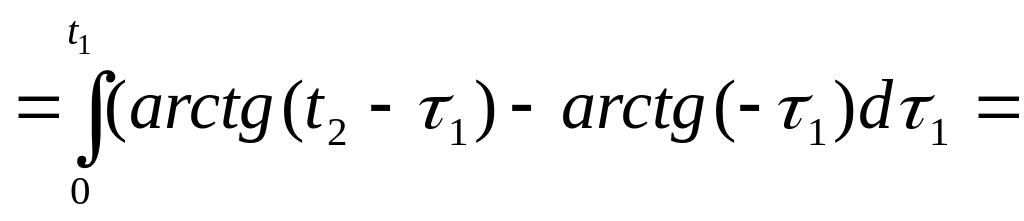
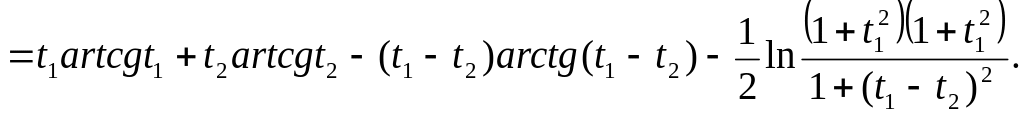
Взаємною кореляційною функцією випадкових процесів та називається невипадкова функція

.

Нормованою взаємною кореляційною функцією випадкових процесів та називається функція

.

Випадкові процеси та називається некорольованими, якщо .

Кореляційна функція суми двох некорельованих випадкових процесів дорівнює суми кореляційних функцій процесів-доданків:

.

Приклад 4. Знайти взаємну кореляційну фунцію випадкових процесів та , де − випадкова величина з дисперсією .

Розв’язання. ,

.

Приклад 5. Нехай та − некорельовані центровані випадкові процеси, . Довести, що

.

Розв’язання. Для центрованого випадкового процесу має місце справедлива формула

.

Оскільки випадкові процеси та є центрованими та некорельованими, то , тобто випадковий процес є також центрованим. Отже,

.

Зокрема покладаючи отримаємо, що

.