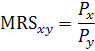4) Нет правильного варианта.

8.32. На основании данных таблицы определите величину предельной нормы замещения товара А товаром В при движении от точки М к точке N:

Наименование продукта	Количество, кг
	С	D	Е	М	N
Товар А	8,0	5,0	3,0	2,0	1,0
Товар В	1,0	2,0	3,0	5,0	8,0

1) 1/3;

2) -1/3;

3) 8;

4) 5.

8.33. Величина предельной полезности составляет 10, изменение количе­ства равно 5. Определите изменение общей полезности:

1) 50;

2) 10;

3) 5;

4) 2.

8.34. Набор товаров А и В, соответствующий каждой точке кривой безраз­личия, приносит потребителю:

1) одинаковую предельную полезность;

2) различную предельную полезность;

3) различную совокупную полезность;

4) одинаковую совокупную полезность.

8.35. На карте безразличия можно изобразить:

1) две кривых безразличия;

2) бесконечно большое число кривых безразличия;

3) бюджетную линию;

4) кривую предельной полезности.

8.36. Каждой точке бюджетной линии соответствует набор товаров А и

В, который:

1) может быть приобретен в течение одного часа;

2) может быть приобретен потребителем при данных затратах на производство;

3) может быть реализован при данных ценах на товары;

4) может быть приобретен потребителем при данном доходе и данных ценах на товары.

8.37. Количество товара А, от которого отказывается потребитель, чтобы приобрести большее количество товара В, называется:

1. предельной нормой потребления;

2. эффектом дохода;

3. предельной нормой замещения;

4. эффектом замещения.

8.38. Точка касания кривой безразличия и бюджетной линии называется:

1) точкой потребительского максимума;

2) точкой потребительского оптимума;

3) точкой потребительского минимума;

4) точкой потребительского экстремума.

8.39. Товары А и В являются взаимозаменяемыми, если:

1) MRS = 0 или ∞

2) MRS = 1;

3) MRS>0;

4) MRS < 0.

8.40. Потребитель максимизирует получаемую им полезность, если выполняется равенство:

2) I =

3) МU =

4) MU = TU_n – TU_n-1

8.41. При построении бюджетной линии на оси ординат откладывают:

1. объем спроса;

2. объем предложения;

3. объем издержек;

4. количество благ.

8.42. MRS_xy не убывает в случае, когда x и y:

1) совершенные субституты;

2) совершенные комплементы;

3) взаимоисключающие блага;

4) все перечисленное верно.

8.43. Если некто потребляет 9 единиц товара при совокупной полезности 38 ютилей, а затем потребляет десятую единицу при совокупной полезности 45 ютилей, то чему равна предельная полезность последней потребляемой единицы товара?

1) 45 ютилей;

2) 10 ютилей;

3) 7 ютилей;

4) 15 ютилей.

8.44. Какое из следующих утверждений о потребительском поведении неверно:

1) потребитель делает выбор, подчиняясь данному бюджетному ограничению;

2) предпочтения не играют значительной роли при определении товара, выбираемого потребителем;

3) цены товаров в потребительском наборе предполагаются заданными;

4) потребитель подбирает подходящие товары в свой потребительский набор так, чтобы максимизировать совокупную полезность.

З А Д А Ч И

Задача 1.

В таблице приведены данные о предельной полезности соответствующих единиц товаров Х и У. На основании этих данных определите такую комбинацию товаров Х и У, которая максимизирует полезность потребителя при условии, что он тратит 320 ден.ед. Цена товара Х - 10 ден.ед., цена товара У – 20 ден.ед.

Единица товара	MUx	MUy
1	180	420
2	160	400
3	150	320
4	110	200
5	100	170
6	80	120
7	60	100
8	40	70
9	10	40

Задача 2.

В таблице приведены данные, характеризующие две кривые безразличия Х и У. Цена товара Х составляет 3 ден.ед., цена товара У – 2 ден.ед. Найдите оптимальное сочетание товаров, если потребитель потратит 48 ден.ед.

Х	У	Рх Ру	MRS
32	12
24	16
18	24
8	48

Задача 3.

В таблице приведены данные о предельной полезности соответствующих единиц товаров X, Y, Z. На основании этих данных определите такую комбинацию товаров X, Y, Z, которая максимизирует полезность потребителя при условии, что он тратит 860 ден.ед.

Цена товара Х – 14 ден.ед., цена товара У – 17 ден.ед, цена товара Z – 5 ден.ед.

Единица товара	MUx	MUx	MZx
1	210	280	175
2	190	250	150
3	175	200	130
4	165	180	110
5	140	160	100
6	120	145	90
7	95	110	80
8	70	90	75
9	45	80	60
10	15	35	45

Задача 4.

Один килограмм сахара стоит 25 ден.ед, а один килограмм гречки 30 ден.ед. Постройте бюджетную линию потребителя, который планирует купить сахара и гречки на 150 ден.ед.

Задача 5.

Один флакон для бритья стоит 80 ден.ед., а один одноразовый станок для бриья стоит 20 ден.ед. постройте бюджетную линию потребителя, если он планирует потратить на эти товары 240 ден.ед.

Задача 6.

Предельная полезность товара А описывается следующей зависимостью

MU_a = (40 – 4Х)_, предельная полезность товара B – (MUb = 84 – 8Y).

При этом Х – это цена товара А, Y – цена товара В. определите пропорции, которые должен потратить потребитель на каждый из данных товаров, при условии, что его расходы составляют 40 ден.единиц.

Задача 7.

Студент читает журнал и слушает музыку с кассет. В таблице показана полезность, которую он получает от потребления различного количества журналов и кассет.

Кол-во	Журналы			Кассеты
	Полезность TU	предельная полезность MU		Полезность TU	предельная полезность MU
1	60			360
2	111			630
3	156			810
4	196			945
5	232			1050
6	265			1140
7	295			1215
8	322			1275
9	347			1320
10	371			1350

Цена журнала 1,5 ден.ед., а цена кассеты 7,5 ден.ед. Предположим, что студент покупает 2 кассеты и 10 журналов:

1) Cколько ден. ед. потратит студент на покупку этого количества кассет и журналов?

2) Какую полезность он получает от потребления такой комбинации товаров?

3) Максимизирует ли студент полезность?

4) Какую полезность он получит, если весь свой бюджет будет тратить на покупку кассет?

5) При какой комбинации двух товаров полезность окажется максимальной?

Задача 8.

Студент еженедельно получает от родителей 20 ден. ед. на карманные расходы (еду и развлечения). Начертите бюджетную линию студента для каждой из следующих ситуаций, обозначая продукты питания по вертикальной оси, а развлечения – по горизонтальной:

Цена продуктов питания, ден.ед.	1	1	2	0,5	2
Цена развлечения, ден.ед.	1	2	1	0,5	2

Как изменится положение бюджетной линии, если Р_х = Р_у = 1 ден.ед., но доход студента увеличится до 25 ден.ед. в неделю?

Задача 9.

Студент получает от родителей 6 ден.ед. в неделю на карманные расходы. Эти ден.ед. он тратит на покупку комиксов и конфет. Каждая книга комиксов стоит 2 ден.ед., а каждая конфета – 1 ден.ед. Полезность для студента каждую неделю складывается из полезности от комиксов и полезности от конфет. Две составляющие функции полезности представлены следующим образом:

Комиксы				Конфеты
Q	TU	MU		Q	TU	MU
0	0			0	0
1	12			1	8
2	22			2	13
3	30			3	17
4	36			4	20
5	41			5	22
6	45			6	23

Заполните пропуски в таблице. Какой потребительский набор выберет студент?

Задача 10.

Выберете в таблице названия уравнений, которые соответствуют данным формулам:

	I=P1X+P2Y
	А	B	C
1. Условие равновесия потребителя
2. Уравнение бюджетной линии
3. Предельная норма замены

Задача 11.

Предельная полезность товара А описывется следующей зависимостью MU_A= (80-8Х), а предельная полезность товара В – (MU_B= 168-16Y). При этом, Х – это цена товара А, Y – цена товара В. Определите пропорции, которые должен потратить потребитель на каждый из данных товаров, при условии, что его расходы составляют 80 ден.ед.

Задача 12.

На рисунке изображены графики кривой безразличия и бюджетной линии:

Q_y

20

E

0 40 Q_x

Если доход потребителя Y=60 ден.ед., а цена товара y равна 3 ден.ед., то как описывается бюджетная линия?

Задача 13.

Независимое потребление двух благ X и Y приносит полезность, величина которой соответствует количеству того или иного блага. Эта зависимость представлена в таблице:

Q	1	2	3	4	5	6	7	8	9	10
TUx	40	76	108	136	160	180	196	208	216	220
TUy	30	57	81	102	120	135	147	156	162	165

Величина дохода потребителя (İ) равна 64, цена блага Х(Р_х) и цена блага Y(P_y) составляет соответственно P_x = 8 и P_y = 3.

1. определите количество блага Х, которое соответствует максимальной полезности при данном уровне дохода.

2. Определите количество блага Y, которое соответствует максимальной полезности при данном уровне дохода.

Задача 14.

Предельная полезность потребления рубашек и ботинок одинаковая. Цена рубашки – 5 ден.ед., а пары ботинок – 10 ден.ед.

Достигается ли равновесие при потреблении этих двух товаров?

91