
- •Етапи аналізу даних.
- •Класифікація типів змінних.
- •Залежні змінні і незалежні.
- •Групування даних.
- •Етапи попередньої обробки даних .
- •2.2 Числові характеристики вибірки.
- •2.3 Перевірка основних гіпотез.
- •Видалення аномальних спостережень.
- •Перевірка випадковості (стохастичності) вибірки.
- •Графічне представлення даних.
- •3.1. Суть кореляційного аналізу
- •3.2 Коефіцієнт детермінації – це є квадрат коефіцієнта кореляції, долю варіації, спільну для двох змінних, іншими словами “степінь” залежності двох змінних.
- •3.3 Частинні коефіцієнти кореляції.
- •3.4. Нелінійна кореляція.
- •4.1 Коефіцієнт рангової кореляції.
- •4.2 Індекс Фехнера.
- •4.3. Кореляційне відношення Пірсона
- •4.4.Коефіцієнт конкордації.
- •Тема: „Регресійний аналіз”.
- •Регресійний аналіз – сукупність статистичних методів, що орієнтовані на дослідження стохастичної залежності однієї змінної y від набору інших змінних .
- •.1Метод найменших квадратів
- •6.1.2 Алгоритм ручного рахунку:
- •6.2 Лінеаризації у випадку криволінійних залежностей
- •6.3 Визначення параметрів парної лінійної регресії для згрупованих даних
- •6.4 Множинна лінійна регресія
- •7.2 Перевірка лінійної регресії.
- •7.3 Розв’язок задач у випадку порушення класичних припущень(мультиколінеарність)
- •Дисперсійний аналіз
- •8.3 Модель 1. Однофакторний дисперсійний аналіз
- •8.4 Двофактоний да
- •8.4.1 Загальна схема двофакторного дисперсійного аналізу(перехідна класифікація з повтореннями)
- •8.4.2 Модель іі
- •Модель ііi.
- •9.1 Коваріаційний аналіз.
- •III. Перевірка гіпотези в умовах ;
- •10.1 Поняття класифікації, задача класифікації
- •10.2. Основні поняття кластерного аналізу та їх застосування
- •10.3 Типи відстаней і мір подібностей
Дисперсійний аналіз
8.1 Дисперсійний аналіз – статистичний метод дослідження вибіркових даних, що проводиться з метою виявлення і оцінки степені впливу на випадкову величину різних, одночасно діючих факторів.
8.2 Розрізняють три моделі дисперсійного аналізу.
Модель
1
– модель
з постійними факторами,
в якій всі
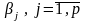 можуть розглядатись, як невідомі сталі.
Величина
можуть розглядатись, як невідомі сталі.
Величина
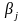 називається адитативною
сталою.
називається адитативною
сталою.
Модель 2 – модель, в якій всі параметри випадкові, за виключенням, можливо одного, що є сталим. Така модель називається моделлю з випадковими факторами.
Модель 3 – це модель, в якій хоч би один параметр випадковий, і хоч би один невипадковий (але не є адитативною сталою). Цю модель називають змішаною моделлю.
8.3 Модель 1. Однофакторний дисперсійний аналіз
Розглянемо випадок, коли на результат вимірювань впливає лише один фактор. Запишемо результати вимірювань деякої ознаки на р об’єктах у вигляді матриці у:
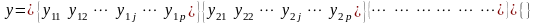 (4)
(4)
Такий запис матриці у означає, що на кожному об’єкті, що відповідає j-ій градації деякого фактору, проведна однакова кількість спостережень, рівна п. Основне рівняння однофакторного дисперсійного аналізу в умовах моделі 1 має вигляд:
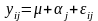 ,
де
,
де
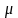 - генеральне середнє,
(5)
- генеральне середнє,
(5)
що
визначаєтья формулою
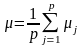 ;
(6)
;
(6)
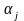 -
ефект j-ї
градації досліджуваного фактора, що
визначається формулою
-
ефект j-ї
градації досліджуваного фактора, що
визначається формулою
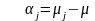 ;
(7)
;
(7)
 -
випадкова незалежна величина , що
відображає вплив на результати
експеременту неконтрольованих факторів
в даному спостереженні.
-
випадкова незалежна величина , що
відображає вплив на результати
експеременту неконтрольованих факторів
в даному спостереженні.
Статистична гіпотеза може бути сформульована наступним чином:
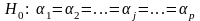 ,
тобто вплив досліджуваного фактора на
всіх рівнях (градаціях) однаковий. Іншими
словами, в умовах гіпотези H0
справедлива рівність:
,
тобто вплив досліджуваного фактора на
всіх рівнях (градаціях) однаковий. Іншими
словами, в умовах гіпотези H0
справедлива рівність:
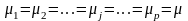 .
.
Перевірка гіпотези здійснюється за наступною схемою:
Обчислюють вибіркові середні
 :
:
 ,
де N=np
(8)
,
де N=np
(8)
Знаходятьсуми квадратів відхилень вибіркових значень від відповідних середніх:
а) суму, яка характеризує зміну, обумовлену досліджуваним фактором:
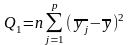 ;
(за факторами)
(9)
;
(за факторами)
(9)
б) суму, яка характеризує зміну всередині кожної градації фактора:
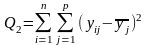 ;
(залишкова)
(10)
;
(залишкова)
(10)
в) суму, яка характеризує загальну зміну ознаки:
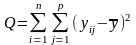 ;
(загальна)
(11)
;
(загальна)
(11)
Якщо
всі допущення про величини
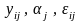 виконуються, то справедлива рівність
виконуються, то справедлива рівність
 .
.
Відповідні дисперсії рівні:
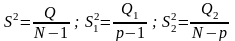 (12)
(12)
Критерій, який використовують для перевірки гіпотези Н0, має вигляд:
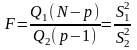 (13)
(13)
При
умові, що гіпотеза Н0
– вірна, розподіл критерію підлягає
закону Фішера (F-розподіл).
Гіпотеза відхиляється, якщо
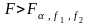 ,
де
,
де
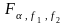 -
таблиця значень F-розподілу
при відповідному рівні значущості
при степенях вільності
-
таблиця значень F-розподілу
при відповідному рівні значущості
при степенях вільності
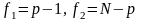 .
.
Модель 2. Однофакторний дисперсійний аналіз
Вибір
об’єктів, що відповідають деяким
градаціям досліджуваного фактору,
рандомізований випадковий вибір
факторів, що визначає випадковий характер
факторних ефектів. Це приводить до зміни
структури основного рівняння однофакторного
дисперсійного аналізу. Воно набере
вигляду
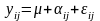 ,
(14)
,
(14)
де - генеральна середня (адитивна стала),
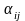 -
значення випадкової величини (відхилення
середнього значення ознаки на j-
му
об’єкті
(mj)
від
генерального середнього, тобто
-
значення випадкової величини (відхилення
середнього значення ознаки на j-
му
об’єкті
(mj)
від
генерального середнього, тобто
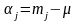 ).
).
Однофакторний ДА з нерівною кількістю спостережень
Загальна схема аналізу лишається такою ж, деякі зміни вносяться лише у формули, за якими обчислюються оцінки середніх і суми квадратів відхилень:
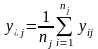 (15)
(15)
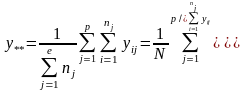 (16)
(16)
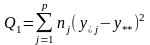 (17)
(17)
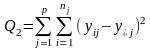 (18)
(18)
 (19)
(19)
Якщо
величина F-критерію
перевищила критичне значення
,
то нульова гіпотеза відхиляється. В
цьому випадку допускають, що існує, в
крайньому разі, хоч би одна пара середніх,
наприклад,
 і
і
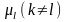 ,
для яких
,
для яких
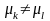 .
.
Більш загальний розв’язок задачі дає метод Шеффе(S- метод). За його допомогою можна побудувати довірчі інтервали для будь-якої лінійної комбінації середніх:
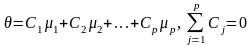 (20)
(20)
Фунція
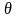 ,
визначена таким чином, називається
контрастом. Вибіркову оцінку
знайдемо шляхом заміни
,
визначена таким чином, називається
контрастом. Вибіркову оцінку
знайдемо шляхом заміни
 величинами
величинами
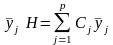 (21)
(21)
Як
і раніше, будемо допускати, що
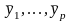 належні і нормально розподілені, а
належні і нормально розподілені, а
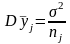 ,
звідси випливає, що
,
звідси випливає, що
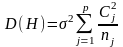 (23)
(23)
Вибірковою оцінкою D(H) є величина
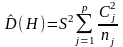 ,
де
(24)
,
де
(24)
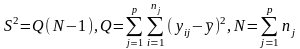 ,
(25)
,
(25)
- об’єм вибірки, що відповідає j-й градації, досліджуваного фактору. Довірчий інтервал велечини визначається наступним співвідношенням:
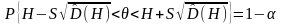 ,
де
,
де
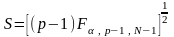 (26)
(26)
Коли
провести
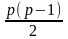 таких порівняннь, то можна виділити всі
„контрастні” значення
таких порівняннь, то можна виділити всі
„контрастні” значення
 і тим самим виявити джерело неоднорідності
середніх.
і тим самим виявити джерело неоднорідності
середніх.
